Black hole

A black hole is a region of spacetime where gravity is so strong that nothing—no particles or even electromagnetic radiation such as light—can escape from it.[6] The theory of general relativity predicts that a sufficiently compact mass can deform spacetime to form a black hole.[7][8] The boundary of the region from which no escape is possible is called the event horizon. Although the event horizon has an enormous effect on the fate and circumstances of an object crossing it, according to general relativity it has no locally detectable features.[9] In many ways, a black hole acts like an ideal black body, as it reflects no light.[10][11] Moreover, quantum field theory in curved spacetime predicts that event horizons emit Hawking radiation, with the same spectrum as a black body of a temperature inversely proportional to its mass. This temperature is on the order of billionths of a kelvin for black holes of stellar mass, making it essentially impossible to observe.

For other uses, see Black hole (disambiguation).

"Frozen star" redirects here. For the hypothetical object, see Frozen star (hypothetical star).

The supermassive black hole at the core of supergiant elliptical galaxy Messier 87, with a mass ~7 billion times the Sun's,[1] as depicted in the first image released by the Event Horizon Telescope (10 April 2019).[2][3][4][5] Visible are the crescent-shaped emission ring and central shadow, which are gravitationally magnified views of the black hole's photon ring and the photon capture zone of its event horizon. The crescent shape arises from the black hole's rotation and relativistic beaming; the shadow is about 2.6 times the diameter of the event horizon.[3]

Objects whose gravitational fields are too strong for light to escape were first considered in the 18th century by John Michell and Pierre-Simon Laplace.[12] The first modern solution of general relativity that would characterize a black hole was found by Karl Schwarzschild in 1916, although its interpretation as a region of space from which nothing can escape was first published by David Finkelstein in 1958. Black holes were long considered a mathematical curiosity; it was not until the 1960s that theoretical work showed they were a generic prediction of general relativity. The discovery of neutron stars by Jocelyn Bell Burnell in 1967 sparked interest in gravitationally collapsed compact objects as a possible astrophysical reality.

Black holes of stellar mass are expected to form when very massive stars collapse at the end of their life cycle. After a black hole has formed, it can continue to grow by absorbing mass from its surroundings. By absorbing other stars and merging with other black holes, supermassive black holes of millions of solar masses (M_☉) may form. There is consensus that supermassive black holes exist in the centers of most galaxies.

The presence of a black hole can be inferred through its interaction with other matter and with electromagnetic radiation such as visible light. Matter that falls onto a black hole can form an external accretion disk heated by friction, forming quasars, some of the brightest objects in the universe. Stars passing too close to a supermassive black hole can be shred into streamers that shine very brightly before being "swallowed."[13] If there are other stars orbiting a black hole, their orbits can be used to determine the black hole's mass and location. Such observations can be used to exclude possible alternatives such as neutron stars. In this way, astronomers have identified numerous stellar black hole candidates in binary systems, and established that the radio source known as Sagittarius A*, at the core of the Milky Way galaxy, contains a supermassive black hole of about 4.3 million solar masses.

On 11 February 2016, the LIGO Scientific Collaboration and the Virgo collaboration announced the first direct detection of gravitational waves, which also represented the first observation of a black hole merger.[14] As of December 2018, eleven gravitational wave events have been observed that originated from ten merging black holes (along with one binary neutron star merger).[15][16] On 10 April 2019, the first direct image of a black hole and its vicinity was published, following observations made by the Event Horizon Telescope in 2017 of the supermassive black hole in Messier 87's galactic centre.[3][17][18]

Simulation of gravitational lensing by a black hole, which distorts the image of a galaxy in the background

Gas cloud being ripped apart by black hole at the centre of the Milky Way (observations from 2006, 2010 and 2013 are shown in blue, green and red, respectively).[19]

History

Simulated view of a black hole in front of the Large Magellanic Cloud. Note the gravitational lensing effect, which produces two enlarged but highly distorted views of the Cloud. Across the top, the Milky Way disk appears distorted into an arc.

The idea of a body so massive that even light could not escape was briefly proposed by astronomical pioneer and English clergyman John Michell in a letter published in November 1784. Michell's simplistic calculations assumed such a body might have the same density as the Sun, and concluded that such a body would form when a star's diameter exceeds the Sun's by a factor of 500, and the surface escape velocity exceeds the usual speed of light. Michell correctly noted that such supermassive but non-radiating bodies might be detectable through their gravitational effects on nearby visible bodies.[20][12][21] Scholars of the time were initially excited by the proposal that giant but invisible stars might be hiding in plain view, but enthusiasm dampened when the wavelike nature of light became apparent in the early nineteenth century.[22]

If light were a wave rather than a "corpuscle", it is unclear what, if any, influence gravity would have on escaping light waves.[12][21] Modern physics discredits Michell's notion of a light ray shooting directly from the surface of a supermassive star, being slowed down by the star's gravity, stopping, and then free-falling back to the star's surface.[23]

General relativity

See also: History of general relativity

In 1915, Albert Einstein developed his theory of general relativity, having earlier shown that gravity does influence light's motion. Only a few months later, Karl Schwarzschild found a solution to the Einstein field equations, which describes the gravitational field of a point mass and a spherical mass.[24] A few months after Schwarzschild, Johannes Droste, a student of Hendrik Lorentz, independently gave the same solution for the point mass and wrote more extensively about its properties.[25][26] This solution had a peculiar behaviour at what is now called the Schwarzschild radius, where it became singular, meaning that some of the terms in the Einstein equations became infinite. The nature of this surface was not quite understood at the time. In 1924, Arthur Eddington showed that the singularity disappeared after a change of coordinates (see Eddington–Finkelstein coordinates), although it took until 1933 for Georges Lemaître to realize that this meant the singularity at the Schwarzschild radius was a non-physical coordinate singularity.[27] Arthur Eddington did however comment on the possibility of a star with mass compressed to the Schwarzschild radius in a 1926 book, noting that Einstein's theory allows us to rule out overly large densities for visible stars like Betelgeuse because "a star of 250 million km radius could not possibly have so high a density as the sun. Firstly, the force of gravitation would be so great that light would be unable to escape from it, the rays falling back to the star like a stone to the earth. Secondly, the red shift of the spectral lines would be so great that the spectrum would be shifted out of existence. Thirdly, the mass would produce so much curvature of the space-time metric that space would close up around the star, leaving us outside (i.e., nowhere)."[28][29]

In 1931, Subrahmanyan Chandrasekhar calculated, using special relativity, that a non-rotating body of electron-degenerate matter above a certain limiting mass (now called the Chandrasekhar limit at 1.4 M_☉) has no stable solutions.[30] His arguments were opposed by many of his contemporaries like Eddington and Lev Landau, who argued that some yet unknown mechanism would stop the collapse.[31] They were partly correct: a white dwarf slightly more massive than the Chandrasekhar limit will collapse into a neutron star,[32] which is itself stable. But in 1939, Robert Oppenheimer and others predicted that neutron stars above another limit (the Tolman–Oppenheimer–Volkoff limit) would collapse further for the reasons presented by Chandrasekhar, and concluded that no law of physics was likely to intervene and stop at least some stars from collapsing to black holes.[33] Their original calculations, based on the Pauli exclusion principle, gave it as 0.7 M_☉; subsequent consideration of strong force-mediated neutron-neutron repulsion raised the estimate to approximately 1.5 M_☉ to 3.0 M_☉.[34] Observations of the neutron star merger GW170817, which is thought to have generated a black hole shortly afterward, have refined the TOV limit estimate to ~2.17 M_☉.[35][36][37][38][39]

Oppenheimer and his co-authors interpreted the singularity at the boundary of the Schwarzschild radius as indicating that this was the boundary of a bubble in which time stopped. This is a valid point of view for external observers, but not for infalling observers. Because of this property, the collapsed stars were called "frozen stars", because an outside observer would see the surface of the star frozen in time at the instant where its collapse takes it to the Schwarzschild radius.[40]

Golden age

In 1958, David Finkelstein identified the Schwarzschild surface as an event horizon, "a perfect unidirectional membrane: causal influences can cross it in only one direction".[41] This did not strictly contradict Oppenheimer's results, but extended them to include the point of view of infalling observers. Finkelstein's solution extended the Schwarzschild solution for the future of observers falling into a black hole. A complete extension had already been found by Martin Kruskal, who was urged to publish it.[42]

These results came at the beginning of the golden age of general relativity, which was marked by general relativity and black holes becoming mainstream subjects of research. This process was helped by the discovery of pulsars by Jocelyn Bell Burnell in 1967,[43][44] which, by 1969, were shown to be rapidly rotating neutron stars.[45] Until that time, neutron stars, like black holes, were regarded as just theoretical curiosities; but the discovery of pulsars showed their physical relevance and spurred a further interest in all types of compact objects that might be formed by gravitational collapse.

In this period more general black hole solutions were found. In 1963, Roy Kerr found the exact solution for a rotating black hole. Two years later, Ezra Newman found the axisymmetric solution for a black hole that is both rotating and electrically charged.[46] Through the work of Werner Israel,[47] Brandon Carter,[48][49] and David Robinson[50] the no-hair theorem emerged, stating that a stationary black hole solution is completely described by the three parameters of the Kerr–Newman metric: mass, angular momentum, and electric charge.[51]

At first, it was suspected that the strange features of the black hole solutions were pathological artifacts from the symmetry conditions imposed, and that the singularities would not appear in generic situations. This view was held in particular by Vladimir Belinsky, Isaak Khalatnikov, and Evgeny Lifshitz, who tried to prove that no singularities appear in generic solutions. However, in the late 1960s Roger Penrose[52] and Stephen Hawking used global techniques to prove that singularities appear generically.[53]

Work by James Bardeen, Jacob Bekenstein, Carter, and Hawking in the early 1970s led to the formulation of black hole thermodynamics.[54] These laws describe the behaviour of a black hole in close analogy to the laws of thermodynamics by relating mass to energy, area to entropy, and surface gravity to temperature. The analogy was completed when Hawking, in 1974, showed that quantum field theory implies that black holes should radiate like a black body with a temperature proportional to the surface gravity of the black hole, predicting the effect now known as Hawking radiation.[55]

Etymology

John Michell used the term "dark star",[56] and in the early 20th century, physicists used the term "gravitationally collapsed object". Science writer Marcia Bartusiak traces the term "black hole" to physicist Robert H. Dicke, who in the early 1960s reportedly compared the phenomenon to the Black Hole of Calcutta, notorious as a prison where people entered but never left alive.[57]

The term "black hole" was used in print by Life and Science News magazines in 1963,[57] and by science journalist Ann Ewing in her article "'Black Holes' in Space", dated 18 January 1964, which was a report on a meeting of the American Association for the Advancement of Science held in Cleveland, Ohio.[58][59]

In December 1967, a student reportedly suggested the phrase "black hole" at a lecture by John Wheeler;[58] Wheeler adopted the term for its brevity and "advertising value", and it quickly caught on,[60] leading some to credit Wheeler with coining the phrase.[61]

Properties and structure

Simple illustration of a non-spinning black hole

The no-hair conjecture postulates that, once it achieves a stable condition after formation, a black hole has only three independent physical properties: mass, charge, and angular momentum; the black hole is otherwise featureless. If the conjecture is true, any two black holes that share the same values for these properties, or parameters, are indistinguishable from one another. The degree to which the conjecture is true for real black holes under the laws of modern physics, is currently an unsolved problem.[51]

These properties are special because they are visible from outside a black hole. For example, a charged black hole repels other like charges just like any other charged object. Similarly, the total mass inside a sphere containing a black hole can be found by using the gravitational analog of Gauss's law, the ADM mass, far away from the black hole.[62] Likewise, the angular momentum can be measured from far away using frame dragging by the gravitomagnetic field.

When an object falls into a black hole, any information about the shape of the object or distribution of charge on it is evenly distributed along the horizon of the black hole, and is lost to outside observers. The behavior of the horizon in this situation is a dissipative system that is closely analogous to that of a conductive stretchy membrane with friction and electrical resistance—the membrane paradigm.[63] This is different from other field theories such as electromagnetism, which do not have any friction or resistivity at the microscopic level, because they are time-reversible. Because a black hole eventually achieves a stable state with only three parameters, there is no way to avoid losing information about the initial conditions: the gravitational and electric fields of a black hole give very little information about what went in. The information that is lost includes every quantity that cannot be measured far away from the black hole horizon, including approximately conserved quantum numbers such as the total baryon number and lepton number. This behavior is so puzzling that it has been called the black hole information loss paradox.[64][65]

Gravitational time dilation around a black hole

Physical properties

The simplest static black holes have mass but neither electric charge nor angular momentum. These black holes are often referred to as Schwarzschild black holes after Karl Schwarzschild who discovered this solution in 1916.[24] According to Birkhoff's theorem, it is the only vacuum solution that is spherically symmetric.[66] This means there is no observable difference at a distance between the gravitational field of such a black hole and that of any other spherical object of the same mass. The popular notion of a black hole "sucking in everything" in its surroundings is therefore correct only near a black hole's horizon; far away, the external gravitational field is identical to that of any other body of the same mass.[67]

Solutions describing more general black holes also exist. Non-rotating charged black holes are described by the Reissner–Nordström metric, while the Kerr metric describes a non-charged rotating black hole. The most general stationary black hole solution known is the Kerr–Newman metric, which describes a black hole with both charge and angular momentum.[68]

While the mass of a black hole can take any positive value, the charge and angular momentum are constrained by the mass. In Planck units, the total electric charge Q and the total angular momentum J are expected to satisfy

${\displaystyle Q^{2}+\left({\tfrac {J}{M}}\right)^{2}\leq M^{2}\,}$

for a black hole of mass M. Black holes with the minimum possible mass satisfying this inequality are called extremal. Solutions of Einstein's equations that violate this inequality exist, but they do not possess an event horizon. These solutions have so-called naked singularities that can be observed from the outside, and hence are deemed unphysical. The cosmic censorship hypothesis rules out the formation of such singularities, when they are created through the gravitational collapse of realistic matter.[7] This is supported by numerical simulations.[69]

Due to the relatively large strength of the electromagnetic force, black holes forming from the collapse of stars are expected to retain the nearly neutral charge of the star. Rotation, however, is expected to be a universal feature of compact astrophysical objects. The black-hole candidate binary X-ray source GRS 1915+105[70] appears to have an angular momentum near the maximum allowed value. That uncharged limit is[71]

${\displaystyle J\leq {\frac {GM^{2}}{c}},}$

allowing definition of a dimensionless spin parameter such that[71]

${\displaystyle 0\leq {\frac {cJ}{GM^{2}}}\leq 1.}$[71][Note 1]

Black hole classifications

Class	Approx. mass	Approx. radius
Supermassive black hole	10^5–10^10 MSun	0.001–400 AU
Intermediate-mass black hole	10^3 MSun	10^3 km ≈ REarth
Stellar black hole	10 MSun	30 km
Micro black hole	up to MMoon	up to 0.1 mm

Black holes are commonly classified according to their mass, independent of angular momentum, J. The size of a black hole, as determined by the radius of the event horizon, or Schwarzschild radius, is proportional to the mass, M, through

${\displaystyle r_{\mathrm {s} }={\frac {2GM}{c^{2}}}\approx 2.95\,{\frac {M}{M_{\mathrm {Sun} }}}~\mathrm {km,} }$

where r_s is the Schwarzschild radius and M_Sun is the mass of the Sun.[73] For a black hole with nonzero spin and/or electric charge, the radius is smaller,[Note 2] until an extremal black hole could have an event horizon close to[74]

${\displaystyle r_{\mathrm {+} }={\frac {GM}{c^{2}}}.}$

Event horizon

Main article: Event horizon

Far away from the black hole, a particle can move in any direction, as illustrated by the set of arrows. It is restricted only by the speed of light.

Closer to the black hole, spacetime starts to deform. There are more paths going towards the black hole than paths moving away.[Note 3]

Inside of the event horizon, all paths bring the particle closer to the center of the black hole. It is no longer possible for the particle to escape.

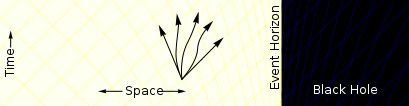
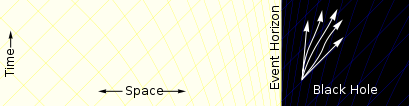
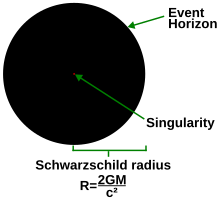
The defining feature of a black hole is the appearance of an event horizon—a boundary in spacetime through which matter and light can pass only inward towards the mass of the black hole. Nothing, not even light, can escape from inside the event horizon. The event horizon is referred to as such because if an event occurs within the boundary, information from that event cannot reach an outside observer, making it impossible to determine whether such an event occurred.[76]

As predicted by general relativity, the presence of a mass deforms spacetime in such a way that the paths taken by particles bend towards the mass.[77] At the event horizon of a black hole, this deformation becomes so strong that there are no paths that lead away from the black hole.[78]

To a distant observer, clocks near a black hole would appear to tick more slowly than those further away from the black hole.[79] Due to this effect, known as gravitational time dilation, an object falling into a black hole appears to slow as it approaches the event horizon, taking an infinite time to reach it.[80] At the same time, all processes on this object slow down, from the view point of a fixed outside observer, causing any light emitted by the object to appear redder and dimmer, an effect known as gravitational redshift.[81] Eventually, the falling object fades away until it can no longer be seen. Typically this process happens very rapidly with an object disappearing from view within less than a second.[82]

On the other hand, indestructible observers falling into a black hole do not notice any of these effects as they cross the event horizon. According to their own clocks, which appear to them to tick normally, they cross the event horizon after a finite time without noting any singular behaviour; in classical general relativity, it is impossible to determine the location of the event horizon from local observations, due to Einstein's equivalence principle.[83][84]

The topology of the event horizon of a black hole at equilibrium is always spherical.[Note 4][87] For non-rotating (static) black holes the geometry of the event horizon is precisely spherical, while for rotating black holes the event horizon is oblate.[88][89][90]

Singularity

Main article: Gravitational singularity

At the center of a black hole, as described by general relativity, may lie a gravitational singularity, a region where the spacetime curvature becomes infinite.[91] For a non-rotating black hole, this region takes the shape of a single point and for a rotating black hole, it is smeared out to form a ring singularity that lies in the plane of rotation.[92] In both cases, the singular region has zero volume. It can also be shown that the singular region contains all the mass of the black hole solution.[93] The singular region can thus be thought of as having infinite density.[94]

Observers falling into a Schwarzschild black hole (i.e., non-rotating and not charged) cannot avoid being carried into the singularity once they cross the event horizon. They can prolong the experience by accelerating away to slow their descent, but only up to a limit.[95] When they reach the singularity, they are crushed to infinite density and their mass is added to the total of the black hole. Before that happens, they will have been torn apart by the growing tidal forces in a process sometimes referred to as spaghettification or the "noodle effect".[96]

In the case of a charged (Reissner–Nordström) or rotating (Kerr) black hole, it is possible to avoid the singularity. Extending these solutions as far as possible reveals the hypothetical possibility of exiting the black hole into a different spacetime with the black hole acting as a wormhole.[97] The possibility of traveling to another universe is, however, only theoretical since any perturbation would destroy this possibility.[98] It also appears to be possible to follow closed timelike curves (returning to one's own past) around the Kerr singularity, which leads to problems with causality like the grandfather paradox.[99] It is expected that none of these peculiar effects would survive in a proper quantum treatment of rotating and charged black holes.[100]

The appearance of singularities in general relativity is commonly perceived as signaling the breakdown of the theory.[101] This breakdown, however, is expected; it occurs in a situation where quantum effects should describe these actions, due to the extremely high density and therefore particle interactions. To date, it has not been possible to combine quantum and gravitational effects into a single theory, although there exist attempts to formulate such a theory of quantum gravity. It is generally expected that such a theory will not feature any singularities.[102][103]

Photon sphere

Main article: Photon sphere

The photon sphere is a spherical boundary of zero thickness in which photons that move on tangents to that sphere would be trapped in a circular orbit about the black hole. For non-rotating black holes, the photon sphere has a radius 1.5 times the Schwarzschild radius. Their orbits would be dynamically unstable, hence any small perturbation, such as a particle of infalling matter, would cause an instability that would grow over time, either setting the photon on an outward trajectory causing it to escape the black hole, or on an inward spiral where it would eventually cross the event horizon.[104]

While light can still escape from the photon sphere, any light that crosses the photon sphere on an inbound trajectory will be captured by the black hole. Hence any light that reaches an outside observer from the photon sphere must have been emitted by objects between the photon sphere and the event horizon.[104]

Ergosphere

Main article: Ergosphere

The ergosphere is a region outside of the event horizon, where objects cannot remain stationary.[105]

Rotating black holes are surrounded by a region of spacetime in which it is impossible to stand still, called the ergosphere. This is the result of a process known as frame-dragging; general relativity predicts that any rotating mass will tend to slightly "drag" along the spacetime immediately surrounding it. Any object near the rotating mass will tend to start moving in the direction of rotation. For a rotating black hole, this effect is so strong near the event horizon that an object would have to move faster than the speed of light in the opposite direction to just stand still.[106]

The ergosphere of a black hole is a volume whose inner boundary is the black hole's event horizon and an outer boundary called the ergosurface, which coincides with the event horizon at the poles but noticeably wider around the equator.[105]

Objects and radiation can escape normally from the ergosphere. Through the Penrose process, objects can emerge from the ergosphere with more energy than they entered. This energy is taken from the rotational energy of the black hole causing the latter to slow.[107] A variation of the Penrose process in the presence of strong magnetic fields, the Blandford–Znajek process is considered a likely mechanism for the enormous luminosity and relativistic jets of quasars and other active galactic nuclei.

Innermost stable circular orbit (ISCO)

Main article: Innermost stable circular orbit

In Newtonian gravity, test particles can stably orbit at arbitrary distances from a central object. In general relativity, however, there exists an innermost stable circular orbit (often called the ISCO), inside of which, any infinitesimal perturbations to a circular orbit will lead to inspiral into the black hole.[108] The location of the ISCO depends on the spin of the black hole, in the case of a Schwarzschild black hole (spin zero) is:

${\displaystyle r_{isco}=3\,r_{s}={\frac {6\,GM}{c^{2}}},}$

and decreases with increasing black hole spin for particles orbiting in the same direction as the spin.[109]

Formation and evolution

Given the bizarre character of black holes, it was long questioned whether such objects could actually exist in nature or whether they were merely pathological solutions to Einstein's equations. Einstein himself wrongly thought black holes would not form, because he held that the angular momentum of collapsing particles would stabilize their motion at some radius.[110] This led the general relativity community to dismiss all results to the contrary for many years. However, a minority of relativists continued to contend that black holes were physical objects,[111] and by the end of the 1960s, they had persuaded the majority of researchers in the field that there is no obstacle to the formation of an event horizon.

Penrose demonstrated that once an event horizon forms, general relativity without quantum mechanics requires that a singularity will form within.[52] Shortly afterwards, Hawking showed that many cosmological solutions that describe the Big Bang have singularities without scalar fields or other exotic matter (see "Penrose–Hawking singularity theorems"). The Kerr solution, the no-hair theorem, and the laws of black hole thermodynamics showed that the physical properties of black holes were simple and comprehensible, making them respectable subjects for research.[112] Conventional black holes are formed by gravitational collapse of heavy objects such as stars, but they can also in theory be formed by other processes.[113][114]

Gravitational collapse

Main article: Gravitational collapse

Gravitational collapse occurs when an object's internal pressure is insufficient to resist the object's own gravity. For stars this usually occurs either because a star has too little "fuel" left to maintain its temperature through stellar nucleosynthesis, or because a star that would have been stable receives extra matter in a way that does not raise its core temperature. In either case the star's temperature is no longer high enough to prevent it from collapsing under its own weight.[115] The collapse may be stopped by the degeneracy pressure of the star's constituents, allowing the condensation of matter into an exotic denser state. The result is one of the various types of compact star. Which type forms depends on the mass of the remnant of the original star left after the outer layers have been blown away. Such explosions and pulsations lead to planetary nebula.[116] This mass can be substantially less than the original star. Remnants exceeding 5 M_☉ are produced by stars that were over 20 M_☉ before the collapse.[115]

If the mass of the remnant exceeds about 3–4 M_☉ (the Tolman–Oppenheimer–Volkoff limit[33]), either because the original star was very heavy or because the remnant collected additional mass through accretion of matter, even the degeneracy pressure of neutrons is insufficient to stop the collapse. No known mechanism (except possibly quark degeneracy pressure, see quark star) is powerful enough to stop the implosion and the object will inevitably collapse to form a black hole.[115]

Artist's impression of supermassive black hole seed[117]

The gravitational collapse of heavy stars is assumed to be responsible for the formation of stellar mass black holes. Star formation in the early universe may have resulted in very massive stars, which upon their collapse would have produced black holes of up to 10³ M_☉. These black holes could be the seeds of the supermassive black holes found in the centers of most galaxies.[118] It has further been suggested that supermassive black holes with typical masses of ~10⁵ M_☉ could have formed from the direct collapse of gas clouds in the young universe.[113] Some candidates for such objects have been found in observations of the young universe.[113]

While most of the energy released during gravitational collapse is emitted very quickly, an outside observer does not actually see the end of this process. Even though the collapse takes a finite amount of time from the reference frame of infalling matter, a distant observer would see the infalling material slow and halt just above the event horizon, due to gravitational time dilation. Light from the collapsing material takes longer and longer to reach the observer, with the light emitted just before the event horizon forms delayed an infinite amount of time. Thus the external observer never sees the formation of the event horizon; instead, the collapsing material seems to become dimmer and increasingly red-shifted, eventually fading away.[119]

Primordial black holes and the Big Bang

Gravitational collapse requires great density. In the current epoch of the universe these high densities are found only in stars, but in the early universe shortly after the Big Bang densities were much greater, possibly allowing for the creation of black holes. High density alone is not enough to allow black hole formation since a uniform mass distribution will not allow the mass to bunch up. In order for primordial black holes to have formed in such a dense medium, there must have been initial density perturbations that could then grow under their own gravity. Different models for the early universe vary widely in their predictions of the scale of these fluctuations. Various models predict the creation of primordial black holes ranging in size from a Planck mass to hundreds of thousands of solar masses.[114]

Despite the early universe being extremely dense—far denser than is usually required to form a black hole—it did not re-collapse into a black hole during the Big Bang. Models for gravitational collapse of objects of relatively constant size, such as stars, do not necessarily apply in the same way to rapidly expanding space such as the Big Bang.[120]

High-energy collisions

Simulated event in the CMS detector: a collision in which a micro black hole may be created

Gravitational collapse is not the only process that could create black holes. In principle, black holes could be formed in high-energy collisions that achieve sufficient density. As of 2002, no such events have been detected, either directly or indirectly as a deficiency of the mass balance in particle accelerator experiments.[121] This suggests that there must be a lower limit for the mass of black holes. Theoretically, this boundary is expected to lie around the Planck mass (m_P=√ħ c/G ≈ 1.2×10¹⁹ GeV/c² ≈ 2.2×10⁻⁸ kg), where quantum effects are expected to invalidate the predictions of general relativity.[122] This would put the creation of black holes firmly out of reach of any high-energy process occurring on or near the Earth. However, certain developments in quantum gravity suggest that the minimum black hole mass could be much lower: some braneworld scenarios for example put the boundary as low as 1 TeV/c².[123] This would make it conceivable for micro black holes to be created in the high-energy collisions that occur when cosmic rays hit the Earth's atmosphere, or possibly in the Large Hadron Collider at CERN. These theories are very speculative, and the creation of black holes in these processes is deemed unlikely by many specialists.[124] Even if micro black holes could be formed, it is expected that they would evaporate in about 10⁻²⁵ seconds, posing no threat to the Earth.[125]

Growth

Once a black hole has formed, it can continue to grow by absorbing additional matter. Any black hole will continually absorb gas and interstellar dust from its surroundings. This is the primary process through which supermassive black holes seem to have grown.[118] A similar process has been suggested for the formation of intermediate-mass black holes found in globular clusters.[126] Black holes can also merge with other objects such as stars or even other black holes. This is thought to have been important, especially in the early growth of supermassive black holes, which could have formed from the aggregation of many smaller objects.[118] The process has also been proposed as the origin of some intermediate-mass black holes.[127][128]

Evaporation

Main article: Hawking radiation

In 1974, Hawking predicted that black holes are not entirely black but emit small amounts of thermal radiation at a temperature ℏ c³/(8 π G M k_B);[55] this effect has become known as Hawking radiation. By applying quantum field theory to a static black hole background, he determined that a black hole should emit particles that display a perfect black body spectrum. Since Hawking's publication, many others have verified the result through various approaches.[129] If Hawking's theory of black hole radiation is correct, then black holes are expected to shrink and evaporate over time as they lose mass by the emission of photons and other particles.[55] The temperature of this thermal spectrum (Hawking temperature) is proportional to the surface gravity of the black hole, which, for a Schwarzschild black hole, is inversely proportional to the mass. Hence, large black holes emit less radiation than small black holes.[130]

A stellar black hole of 1 M_☉ has a Hawking temperature of 62 nanokelvins.[131] This is far less than the 2.7 K temperature of the cosmic microwave background radiation. Stellar-mass or larger black holes receive more mass from the cosmic microwave background than they emit through Hawking radiation and thus will grow instead of shrinking.[132] To have a Hawking temperature larger than 2.7 K (and be able to evaporate), a black hole would need a mass less than the Moon. Such a black hole would have a diameter of less than a tenth of a millimeter.[133]

If a black hole is very small, the radiation effects are expected to become very strong. A black hole with the mass of a car would have a diameter of about 10⁻²⁴ m and take a nanosecond to evaporate, during which time it would briefly have a luminosity of more than 200 times that of the Sun. Lower-mass black holes are expected to evaporate even faster; for example, a black hole of mass 1 TeV/c² would take less than 10⁻⁸⁸ seconds to evaporate completely. For such a small black hole, quantum gravitation effects are expected to play an important role and could hypothetically make such a small black hole stable, although current developments in quantum gravity do not indicate this is the case.[134][135]

The Hawking radiation for an astrophysical black hole is predicted to be very weak and would thus be exceedingly difficult to detect from Earth. A possible exception, however, is the burst of gamma rays emitted in the last stage of the evaporation of primordial black holes. Searches for such flashes have proven unsuccessful and provide stringent limits on the possibility of existence of low mass primordial black holes.[136] NASA's Fermi Gamma-ray Space Telescope launched in 2008 will continue the search for these flashes.[137]

If black holes evaporate via Hawking radiation, a solar mass black hole will evaporate (beginning once the temperature of the cosmic microwave background drops below that of the black hole) over a period of 10⁶⁴ years.[138] A supermassive black hole with a mass of 10¹¹ (100 billion) M_☉ will evaporate in around 2×10¹⁰⁰ years.[139] Some monster black holes in the universe are predicted to continue to grow up to perhaps 10¹⁴ M_☉ during the collapse of superclusters of galaxies. Even these would evaporate over a timescale of up to 10¹⁰⁶ years.[138]

Observational evidence

Messier 87 galaxy – home of the first imaged black hole

context

closeup

supermassive black hole

By nature, black holes do not themselves emit any electromagnetic radiation other than the hypothetical Hawking radiation, so astrophysicists searching for black holes must generally rely on indirect observations. For example, a black hole's existence can sometimes be inferred by observing its gravitational influence upon its surroundings.[140]

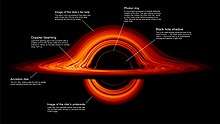
On 10 April 2019 an image was released of a black hole, which is seen in magnified fashion because the light paths near the event horizon are highly bent. The dark shadow in the middle results from light paths absorbed by the black hole. The image is in false color, as the detected light halo in this image is not in the visible spectrum, but radio waves.

This artist's impression depicts the paths of photons in the vicinity of a black hole. The gravitational bending and capture of light by the event horizon is the cause of the shadow captured by the Event Horizon Telescope.

The Event Horizon Telescope (EHT), is an active program that directly observes the immediate environment of the event horizon of black holes, such as the black hole at the centre of the Milky Way. In April 2017, EHT began observation of the black hole in the center of Messier 87.[141] "In all, eight radio observatories on six mountains and four continents observed the galaxy in Virgo on and off for 10 days in April 2017" to provide the data yielding the image two years later in April 2019.[142] After two years of data processing, EHT released the first direct image of a black hole, specifically the supermassive black hole that lies in the center of the aforementioned galaxy.[143][144] What is visible is not the black hole, which shows as black because of the loss of all light within this dark region, rather it is the gases at the edge of the event horizon, which are displayed as orange or red, that define the black hole.[145]

The brightening of this material in the 'bottom' half of the processed EHT image is thought to be caused by Doppler beaming, whereby material approaching the viewer at relativistic speeds is perceived as brighter than material moving away. In the case of a black hole this phenomenon implies that the visible material is rotating at relativistic speeds (>1,000 km/s), the only speeds at which it is possible to centrifugally balance the immense gravitational attraction of the singularity, and thereby remain in orbit above the event horizon. This configuration of bright material implies that the EHT observed M87* from a perspective catching the black hole's accretion disc nearly edge-on, as the whole system rotated clockwise.[146] However, the extreme gravitational lensing associated with black holes produces the illusion of a perspective that sees the accretion disc from above. In reality, most of the ring in the EHT image was created when the light emitted by the far side of the accretion disc bent around the black hole's gravity well and escaped such that most of the possible perspectives on M87* can see the entire disc, even that directly behind the "shadow".

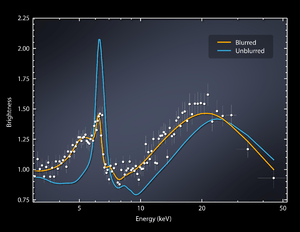
Prior to this, in 2015, the EHT detected magnetic fields just outside the event horizon of Sagittarius A*, and even discerned some of their properties. The field lines that pass through the accretion disc were found to be a complex mixture of ordered and tangled. The existence of magnetic fields had been predicted by theoretical studies of black holes.[147][148]

Predicted appearance of non-rotating black hole with toroidal ring of ionised matter, such as has been proposed[149] as a model for Sagittarius A*. The asymmetry is due to the Doppler effect resulting from the enormous orbital speed needed for centrifugal balance of the very strong gravitational attraction of the hole.

Detection of gravitational waves from merging black holes

On 14 September 2015 the LIGO gravitational wave observatory made the first-ever successful direct observation of gravitational waves.[14][150] The signal was consistent with theoretical predictions for the gravitational waves produced by the merger of two black holes: one with about 36 solar masses, and the other around 29 solar masses.[14][151] This observation provides the most concrete evidence for the existence of black holes to date. For instance, the gravitational wave signal suggests that the separation of the two objects prior to the merger was just 350 km (or roughly four times the Schwarzschild radius corresponding to the inferred masses). The objects must therefore have been extremely compact, leaving black holes as the most plausible interpretation.[14]

More importantly, the signal observed by LIGO also included the start of the post-merger ringdown, the signal produced as the newly formed compact object settles down to a stationary state. Arguably, the ringdown is the most direct way of observing a black hole.[152] From the LIGO signal it is possible to extract the frequency and damping time of the dominant mode of the ringdown. From these it is possible to infer the mass and angular momentum of the final object, which match independent predictions from numerical simulations of the merger.[153] The frequency and decay time of the dominant mode are determined by the geometry of the photon sphere. Hence, observation of this mode confirms the presence of a photon sphere, however it cannot exclude possible exotic alternatives to black holes that are compact enough to have a photon sphere.[152]

The observation also provides the first observational evidence for the existence of stellar-mass black hole binaries. Furthermore, it is the first observational evidence of stellar-mass black holes weighing 25 solar masses or more.[154]

Since then many more gravitational wave events have since been observed.[16]

Proper motions of stars orbiting Sagittarius A*

The proper motions of stars near the center of our own Milky Way provide strong observational evidence that these stars are orbiting a supermassive black hole.[155] Since 1995, astronomers have tracked the motions of 90 stars orbiting an invisible object coincident with the radio source Sagittarius A*. By fitting their motions to Keplerian orbits, the astronomers were able to infer, in 1998, that a 2.6 million M_☉ object must be contained in a volume with a radius of 0.02 light-years to cause the motions of those stars.[156] Since then, one of the stars—called S2—has completed a full orbit. From the orbital data, astronomers were able to refine the calculations of the mass to 4.3 million M_☉ and a radius of less than 0.002 light years for the object causing the orbital motion of those stars.[155] The upper limit on the object's size is still too large to test whether it is smaller than its Schwarzschild radius; nevertheless, these observations strongly suggest that the central object is a supermassive black hole as there are no other plausible scenarios for confining so much invisible mass into such a small volume.[156] Additionally, there is some observational evidence that this object might possess an event horizon, a feature unique to black holes.[157]

Accretion of matter

See also: Accretion disk

Black hole with corona, X-ray source (artist's concept)[158]

Due to conservation of angular momentum,[159] gas falling into the gravitational well created by a massive object will typically form a disk-like structure around the object. Artists' impressions such as the accompanying representation of a black hole with corona commonly depict the black hole as if it were a flat-space body hiding the part of the disk just behind it, but in reality gravitational lensing would greatly distort the image of the accretion disk.[160]

NASA simulated view from outside the horizon of a Schwarzschild black hole lit by a thin accretion disk.

Within such a disk, friction would cause angular momentum to be transported outward, allowing matter to fall further inward, thus releasing potential energy and increasing the temperature of the gas.[161]

Blurring of X-rays near black hole (NuSTAR; 12 August 2014)[158]

When the accreting object is a neutron star or a black hole, the gas in the inner accretion disk orbits at very high speeds because of its proximity to the compact object. The resulting friction is so significant that it heats the inner disk to temperatures at which it emits vast amounts of electromagnetic radiation (mainly X-rays). These bright X-ray sources may be detected by telescopes. This process of accretion is one of the most efficient energy-producing processes known; up to 40% of the rest mass of the accreted material can be emitted as radiation.[161] (In nuclear fusion only about 0.7% of the rest mass will be emitted as energy.) In many cases, accretion disks are accompanied by relativistic jets that are emitted along the poles, which carry away much of the energy. The mechanism for the creation of these jets is currently not well understood, in part due to insufficient data.[162]

As such, many of the universe's more energetic phenomena have been attributed to the accretion of matter on black holes. In particular, active galactic nuclei and quasars are believed to be the accretion disks of supermassive black holes.[163] Similarly, X-ray binaries are generally accepted to be binary star systems in which one of the two stars is a compact object accreting matter from its companion.[163] It has also been suggested that some ultraluminous X-ray sources may be the accretion disks of intermediate-mass black holes.[164]

In November 2011 the first direct observation of a quasar accretion disk around a supermassive black hole was reported.[165][166]

X-ray binaries

See also: X-ray binary

A Chandra X-Ray Observatory image of Cygnus X-1, which was the first strong black hole candidate discovered

X-ray binaries are binary star systems that emit a majority of their radiation in the X-ray part of the spectrum. These X-ray emissions are generally thought to result when one of the stars (compact object) accretes matter from another (regular) star. The presence of an ordinary star in such a system provides an opportunity for studying the central object and to determine if it might be a black hole.[163]

If such a system emits signals that can be directly traced back to the compact object, it cannot be a black hole. The absence of such a signal does, however, not exclude the possibility that the compact object is a neutron star. By studying the companion star it is often possible to obtain the orbital parameters of the system and to obtain an estimate for the mass of the compact object. If this is much larger than the Tolman–Oppenheimer–Volkoff limit (the maximum mass a star can have without collapsing) then the object cannot be a neutron star and is generally expected to be a black hole.[163]

The first strong candidate for a black hole, Cygnus X-1, was discovered in this way by Charles Thomas Bolton,[167] Louise Webster and Paul Murdin[168] in 1972.[169][170] Some doubt, however, remained due to the uncertainties that result from the companion star being much heavier than the candidate black hole. Currently, better candidates for black holes are found in a class of X-ray binaries called soft X-ray transients. In this class of system, the companion star is of relatively low mass allowing for more accurate estimates of the black hole mass. Moreover, these systems actively emit X-rays for only several months once every 10–50 years. During the period of low X-ray emission (called quiescence), the accretion disk is extremely faint allowing detailed observation of the companion star during this period. One of the best such candidates is V404 Cygni.[163]

Quasi-periodic oscillations

The X-ray emissions from accretion disks sometimes flicker at certain frequencies. These signals are called quasi-periodic oscillations and are thought to be caused by material moving along the inner edge of the accretion disk (the innermost stable circular orbit). As such their frequency is linked to the mass of the compact object. They can thus be used as an alternative way to determine the mass of candidate black holes.[171]

Galactic nuclei

See also: Active galactic nucleus

Magnetic waves, called Alfvén S-waves, flow from the base of black hole jets.

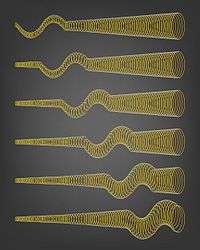
Astronomers use the term "active galaxy" to describe galaxies with unusual characteristics, such as unusual spectral line emission and very strong radio emission. Theoretical and observational studies have shown that the activity in these active galactic nuclei (AGN) may be explained by the presence of supermassive black holes, which can be millions of times more massive than stellar ones. The models of these AGN consist of a central black hole that may be millions or billions of times more massive than the Sun; a disk of gas and dust called an accretion disk; and two jets perpendicular to the accretion disk.[172][173]

Detection of unusually bright X-Ray flare from Sagittarius A*, a black hole in the center of the Milky Way galaxy on 5 January 2015[174]

Although supermassive black holes are expected to be found in most AGN, only some galaxies' nuclei have been more carefully studied in attempts to both identify and measure the actual masses of the central supermassive black hole candidates. Some of the most notable galaxies with supermassive black hole candidates include the Andromeda Galaxy, M32, M87, NGC 3115, NGC 3377, NGC 4258, NGC 4889, NGC 1277, OJ 287, APM 08279+5255 and the Sombrero Galaxy.[175]

It is now widely accepted that the center of nearly every galaxy, not just active ones, contains a supermassive black hole.[176] The close observational correlation between the mass of this hole and the velocity dispersion of the host galaxy's bulge, known as the M-sigma relation, strongly suggests a connection between the formation of the black hole and the galaxy itself.[177]

Simulation of gas cloud after close approach to the black hole at the centre of the Milky Way.[178]

Microlensing (proposed)

Another way the black hole nature of an object may be tested in the future is through observation of effects caused by a strong gravitational field in their vicinity. One such effect is gravitational lensing: The deformation of spacetime around a massive object causes light rays to be deflected much as light passing through an optic lens. Observations have been made of weak gravitational lensing, in which light rays are deflected by only a few arcseconds. However, it has never been directly observed for a black hole.[179] One possibility for observing gravitational lensing by a black hole would be to observe stars in orbit around the black hole. There are several candidates for such an observation in orbit around Sagittarius A*.[179]

Alternatives

See also: Exotic star

The evidence for stellar black holes strongly relies on the existence of an upper limit for the mass of a neutron star. The size of this limit heavily depends on the assumptions made about the properties of dense matter. New exotic phases of matter could push up this bound.[163] A phase of free quarks at high density might allow the existence of dense quark stars,[180] and some supersymmetric models predict the existence of Q stars.[181] Some extensions of the standard model posit the existence of preons as fundamental building blocks of quarks and leptons, which could hypothetically form preon stars.[182] These hypothetical models could potentially explain a number of observations of stellar black hole candidates. However, it can be shown from arguments in general relativity that any such object will have a maximum mass.[163]

Since the average density of a black hole inside its Schwarzschild radius is inversely proportional to the square of its mass, supermassive black holes are much less dense than stellar black holes (the average density of a 10⁸ M_☉ black hole is comparable to that of water).[163] Consequently, the physics of matter forming a supermassive black hole is much better understood and the possible alternative explanations for supermassive black hole observations are much more mundane. For example, a supermassive black hole could be modelled by a large cluster of very dark objects. However, such alternatives are typically not stable enough to explain the supermassive black hole candidates.[163]

The evidence for the existence of stellar and supermassive black holes implies that in order for black holes to not form, general relativity must fail as a theory of gravity, perhaps due to the onset of quantum mechanical corrections. A much anticipated feature of a theory of quantum gravity is that it will not feature singularities or event horizons and thus black holes would not be real artifacts.[183] For example, in the fuzzball model based on string theory, the individual states of a black hole solution do not generally have an event horizon or singularity, but for a classical/semi-classical observer the statistical average of such states appears just as an ordinary black hole as deduced from general relativity.[184]

A few theoretical objects have been conjectured to match observations of astronomical black hole candidates identically or near-identically, but which function via a different mechanism. These include the gravastar, the black star,[185] and the dark-energy star.[186]

Open questions

Entropy and thermodynamics

Further information: Black hole thermodynamics

S = 1/4 c³k/Għ A

The formula for the Bekenstein–Hawking entropy (S) of a black hole, which depends on the area of the black hole (A). The constants are the speed of light (c), the Boltzmann constant (k), Newton's constant (G), and the reduced Planck constant (ħ). In Planck units, this reduces to S = A/4.

In 1971, Hawking showed under general conditions[Note 5] that the total area of the event horizons of any collection of classical black holes can never decrease, even if they collide and merge.[187] This result, now known as the second law of black hole mechanics, is remarkably similar to the second law of thermodynamics, which states that the total entropy of an isolated system can never decrease. As with classical objects at absolute zero temperature, it was assumed that black holes had zero entropy. If this were the case, the second law of thermodynamics would be violated by entropy-laden matter entering a black hole, resulting in a decrease of the total entropy of the universe. Therefore, Bekenstein proposed that a black hole should have an entropy, and that it should be proportional to its horizon area.[188]

The link with the laws of thermodynamics was further strengthened by Hawking's discovery that quantum field theory predicts that a black hole radiates blackbody radiation at a constant temperature. This seemingly causes a violation of the second law of black hole mechanics, since the radiation will carry away energy from the black hole causing it to shrink. The radiation, however also carries away entropy, and it can be proven under general assumptions that the sum of the entropy of the matter surrounding a black hole and one quarter of the area of the horizon as measured in Planck units is in fact always increasing. This allows the formulation of the first law of black hole mechanics as an analogue of the first law of thermodynamics, with the mass acting as energy, the surface gravity as temperature and the area as entropy.[188]

One puzzling feature is that the entropy of a black hole scales with its area rather than with its volume, since entropy is normally an extensive quantity that scales linearly with the volume of the system. This odd property led Gerard 't Hooft and Leonard Susskind to propose the holographic principle, which suggests that anything that happens in a volume of spacetime can be described by data on the boundary of that volume.[189]

Although general relativity can be used to perform a semi-classical calculation of black hole entropy, this situation is theoretically unsatisfying. In statistical mechanics, entropy is understood as counting the number of microscopic configurations of a system that have the same macroscopic qualities (such as mass, charge, pressure, etc.). Without a satisfactory theory of quantum gravity, one cannot perform such a computation for black holes. Some progress has been made in various approaches to quantum gravity. In 1995, Andrew Strominger and Cumrun Vafa showed that counting the microstates of a specific supersymmetric black hole in string theory reproduced the Bekenstein–Hawking entropy.[190] Since then, similar results have been reported for different black holes both in string theory and in other approaches to quantum gravity like loop quantum gravity.[191]

Information loss paradox

Main article: Black hole information paradox

Unsolved problem in physics: Is physical information lost in black holes? (more unsolved problems in physics)

Because a black hole has only a few internal parameters, most of the information about the matter that went into forming the black hole is lost. Regardless of the type of matter which goes into a black hole, it appears that only information concerning the total mass, charge, and angular momentum are conserved. As long as black holes were thought to persist forever this information loss is not that problematic, as the information can be thought of as existing inside the black hole, inaccessible from the outside, but represented on the event horizon in accordance with the holographic principle. However, black holes slowly evaporate by emitting Hawking radiation. This radiation does not appear to carry any additional information about the matter that formed the black hole, meaning that this information appears to be gone forever.[192]

The question whether information is truly lost in black holes (the black hole information paradox) has divided the theoretical physics community (see Thorne–Hawking–Preskill bet). In quantum mechanics, loss of information corresponds to the violation of a property called unitarity, and it has been argued that loss of unitarity would also imply violation of conservation of energy,[193] though this has also been disputed.[194] Over recent years evidence has been building that indeed information and unitarity are preserved in a full quantum gravitational treatment of the problem.[195]

One attempt to resolve the black hole information paradox is known as black hole complementarity. In 2012, the "firewall paradox" was introduced with the goal of demonstrating that black hole complementarity fails to solve the information paradox. According to quantum field theory in curved spacetime, a single emission of Hawking radiation involves two mutually entangled particles. The outgoing particle escapes and is emitted as a quantum of Hawking radiation; the infalling particle is swallowed by the black hole. Assume a black hole formed a finite time in the past and will fully evaporate away in some finite time in the future. Then, it will emit only a finite amount of information encoded within its Hawking radiation. According to research by physicists like Don Page[196][197] and Leonard Susskind, there will eventually be a time by which an outgoing particle must be entangled with all the Hawking radiation the black hole has previously emitted. This seemingly creates a paradox: a principle called "monogamy of entanglement" requires that, like any quantum system, the outgoing particle cannot be fully entangled with two other systems at the same time; yet here the outgoing particle appears to be entangled both with the infalling particle and, independently, with past Hawking radiation.[198] In order to resolve this contradiction, physicists may eventually be forced to give up one of three time-tested principles: Einstein's equivalence principle, unitarity, or local quantum field theory. One possible solution, which violates the equivalence principle, is that a "firewall" destroys incoming particles at the event horizon.[199] In general, which if any of these assumptions should be abandoned remains a topic of debate.[194]

See also

• Binary black hole
• Black brane
• Black Hole Initiative
• Black hole starship
• Black holes in fiction
• Black string
• Blanet
• BTZ black hole
• Kugelblitz (astrophysics)
• List of black holes
• List of nearest black holes
• Outline of black holes
• Sonic black hole
• Susskind-Hawking battle
• Timeline of black hole physics
• White hole

Notes

1. The value of cJ/GM² can exceed 1 for objects other than black holes. The largest value known for a neutron star is ≤ 0.4, and commonly used equations of state would limit that value to < 0.7.[72]
2. The (outer) event horizon radius scales as: ${\displaystyle M+{\sqrt {M^{2}-{(J/M)}^{2}-Q^{2}}}.}$
3. The set of possible paths, or more accurately the future light cone containing all possible world lines (in this diagram the light cone is represented by the V-shaped region bounded by arrows representing light ray world lines), is tilted in this way in Eddington–Finkelstein coordinates (the diagram is a "cartoon" version of an Eddington–Finkelstein coordinate diagram), but in other coordinates the light cones are not tilted in this way, for example in Schwarzschild coordinates they simply narrow without tilting as one approaches the event horizon, and in Kruskal–Szekeres coordinates the light cones do not change shape or orientation at all.[75]
4. This is true only for four-dimensional spacetimes. In higher dimensions more complicated horizon topologies like a black ring are possible.[85][86]
5. In particular, he assumed that all matter satisfies the weak energy condition.

References

1. Oldham, L. J.; Auger, M. W. (March 2016). "Galaxy structure from multiple tracers – II. M87 from parsec to megaparsec scales". Monthly Notices of the Royal Astronomical Society. 457 (1): 421–439. arXiv:1601.01323. Bibcode:2016MNRAS.457..421O. doi:10.1093/mnras/stv2982.
2. Overbye, Dennis (10 April 2019). "Black Hole Picture Revealed for the First Time – Astronomers at last have captured an image of the darkest entities in the cosmos – Comments". The New York Times. Retrieved 10 April 2019.
3. Event Horizon Telescope, The (2019). "First M87 Event Horizon Telescope Results. I. The Shadow of the Supermassive Black Hole". The Astrophysical Journal. 875 (1): L1. arXiv:1906.11238. Bibcode:2019ApJ...875L...1E. doi:10.3847/2041-8213/ab0ec7.
4. Landau, Elizabeth (10 April 2019). "Black Hole Image Makes History". NASA. Retrieved 10 April 2019.
5. "The woman behind first black hole image". bbc.co.uk. BBC News. 11 April 2019.
6. Wald 1984, pp. 299–300
7. Wald, R. M. (1997). "Gravitational Collapse and Cosmic Censorship". In Iyer, B. R.; Bhawal, B. (eds.). Black Holes, Gravitational Radiation and the Universe. Springer. pp. 69–86. arXiv:gr-qc/9710068. doi:10.1007/978-94-017-0934-7. ISBN 978-9401709347.
8. Overbye, Dennis (8 June 2015). "Black Hole Hunters". NASA. Archived from the original on 9 June 2015. Retrieved 8 June 2015.
9. Hamilton, A. "Journey into a Schwarzschild black hole". jila.colorado.edu. Retrieved 28 June 2020.
10. Schutz, Bernard F. (2003). Gravity from the ground up. Cambridge University Press. p. 110. ISBN 978-0-521-45506-0. Archived from the original on 2 December 2016.
11. Davies, P. C. W. (1978). "Thermodynamics of Black Holes" (PDF). Reports on Progress in Physics. 41 (8): 1313–1355. Bibcode:1978RPPh...41.1313D. doi:10.1088/0034-4885/41/8/004. Archived from the original (PDF) on 10 May 2013.CS1 maint: ref=harv (link)
12. Montgomery, Colin; Orchiston, Wayne; Whittingham, Ian (2009). "Michell, Laplace and the origin of the black hole concept". Journal of Astronomical History and Heritage. 12 (2): 90–96. Bibcode:2009JAHH...12...90M.
13. Clery D (2020). "Black holes caught in the act of swallowing stars". Science. 367 (6477): 495. Bibcode:2020Sci...367..495C. doi:10.1126/science.367.6477.495. PMID 32001633.
14. Abbott, B.P.; et al. (2016). "Observation of Gravitational Waves from a Binary Black Hole Merger". Phys. Rev. Lett. 116 (6): 061102. arXiv:1602.03837. Bibcode:2016PhRvL.116f1102A. doi:10.1103/PhysRevLett.116.061102. PMID 26918975.
15. Siegel, Ethan. "Five Surprising Truths About Black Holes From LIGO". Forbes. Retrieved 12 April 2019.
16. "Detection of gravitational waves". LIGO. Retrieved 9 April 2018.
17. Bouman, Katherine L.; Johnson, Michael D.; Zoran, Daniel; Fish, Vincent L.; Doeleman, Sheperd S.; Freeman, William T. (2016). "Computational Imaging for VLBI Image Reconstruction". 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR). pp. 913–922. arXiv:1512.01413. doi:10.1109/CVPR.2016.105. hdl:1721.1/103077. ISBN 978-1-4673-8851-1.
18. Gardiner, Aidan (12 April 2018). "When a Black Hole Finally Reveals Itself, It Helps to Have Our Very Own Cosmic Reporter – Astronomers announced Wednesday that they had captured the first image of a black hole. The Times's Dennis Overbye answers readers' questions". The New York Times. Retrieved 15 April 2019.
19. "Ripped Apart by a Black Hole". ESO Press Release. Archived from the original on 21 July 2013. Retrieved 19 July 2013.
20. Michell, J. (1784). "On the Means of Discovering the Distance, Magnitude, &c. of the Fixed Stars, in Consequence of the Diminution of the Velocity of Their Light, in Case Such a Diminution Should be Found to Take Place in any of Them, and Such Other Data Should be Procured from Observations, as Would be Farther Necessary for That Purpose. By the Rev. John Michell, B. D. F. R. S. In a Letter to Henry Cavendish, Esq. F. R. S. and A. S". Philosophical Transactions of the Royal Society. 74: 35–57. Bibcode:1784RSPT...74...35M. doi:10.1098/rstl.1784.0008. JSTOR 106576.CS1 maint: ref=harv (link)
21. Thorne 1994, pp. 123–124
22. Slayter, Elizabeth M.; Slayter, Henry S. (1992). Light and Electron Microscopy. Cambridge University Press. ISBN 978-0-521-33948-3. Archived from the original on 30 November 2017.
23. Crass, Institute of Astronomy – Design by D.R. Wilkins and S.J. "Light escaping from black holes". www.ast.cam.ac.uk. Retrieved 10 March 2018.
24. Schwarzschild, K. (1916). "Über das Gravitationsfeld eines Massenpunktes nach der Einsteinschen Theorie". Sitzungsberichte der Königlich Preussischen Akademie der Wissenschaften. 7: 189–196. Bibcode:1916SPAW.......189S.CS1 maint: ref=harv (link)

    • Translation: Antoci, S.; Loinger, A. (1999). "On the gravitational field of a mass point according to Einstein's theory". arXiv:physics/9905030. Bibcode:1999physics...5030S. Cite journal requires |journal= (help) and Schwarzschild, K. (1916). "Über das Gravitationsfeld einer Kugel aus inkompressibler Flüssigkeit nach der Einsteinschen Theorie". Sitzungsberichte der Königlich Preussischen Akademie der Wissenschaften. 18: 424–434. Bibcode:1916skpa.conf..424S.CS1 maint: ref=harv (link)
    • Translation: Antoci, S. (1999). "On the gravitational field of a sphere of incompressible fluid according to Einstein's theory". arXiv:physics/9912033. Bibcode:1999physics..12033S. Cite journal requires |journal= (help)

25. Droste, J. (1917). "On the field of a single centre in Einstein's theory of gravitation, and the motion of a particle in that field" (PDF). Proceedings Royal Academy Amsterdam. 19 (1): 197–215. Archived (PDF) from the original on 18 May 2013.CS1 maint: ref=harv (link)
26. Kox, A. J. (1992). "General Relativity in the Netherlands: 1915–1920". In Eisenstaedt, Jean; Kox, A. J. (eds.). Studies in the history of general relativity. Birkhäuser. p. 41. ISBN 978-0-8176-3479-7.
27. 't Hooft, G. (2009). "Introduction to the Theory of Black Holes" (PDF). Institute for Theoretical Physics / Spinoza Institute: 47–48. Archived (PDF) from the original on 21 May 2009. Cite journal requires |journal= (help)CS1 maint: ref=harv (link)
28. Eddington, Arthur (1926). The Internal Constitution of the Stars. Science. 52. Cambridge University Press. pp. 233–40. doi:10.1126/science.52.1341.233. ISBN 978-0-521-33708-3. PMID 17747682. Archived from the original on 11 August 2016.
29. Thorne, Kip S.; Hawking, Stephen (1994). Black Holes and Time Warps: Einstein's Outrageous Legacy. W. W. Norton & Company. pp. 134–135. ISBN 978-0-393-31276-8. Retrieved 12 April 2019. The first conclusion was the Newtonian version of light not escaping; the second was a semi-accurate, relativistic description; and the third was typical Eddingtonian hyperbole ... when a star is as small as the critical circumference, the curvature is strong but not infinite, and space is definitely not wrapped around the star. Eddington may have known this, but his description made a good story, and it captured in a whimsical way the spirit of Schwarzschild's spacetime curvature."
30. Venkataraman, G. (1992). Chandrasekhar and his limit. Universities Press. p. 89. ISBN 978-81-7371-035-3. Archived from the original on 11 August 2016.
31. Detweiler, S. (1981). "Resource letter BH-1: Black holes". American Journal of Physics. 49 (5): 394–400. Bibcode:1981AmJPh..49..394D. doi:10.1119/1.12686.CS1 maint: ref=harv (link)
32. Harpaz, A. (1994). Stellar evolution. A K Peters. p. 105. ISBN 978-1-56881-012-6. Archived from the original on 11 August 2016.
33. Oppenheimer, J. R.; Volkoff, G. M. (1939). "On Massive Neutron Cores". Physical Review. 55 (4): 374–381. Bibcode:1939PhRv...55..374O. doi:10.1103/PhysRev.55.374.CS1 maint: ref=harv (link)
34. Bombaci, I. (1996). "The Maximum Mass of a Neutron Star". Astronomy and Astrophysics. 305: 871–877. Bibcode:1996A&A...305..871B.
35. Cho, A. (16 February 2018). "A weight limit emerges for neutron stars". Science. 359 (6377): 724–725. Bibcode:2018Sci...359..724C. doi:10.1126/science.359.6377.724. PMID 29449468.
36. Margalit, B.; Metzger, B. D. (1 December 2017). "Constraining the Maximum Mass of Neutron Stars from Multi-messenger Observations of GW170817". The Astrophysical Journal. 850 (2): L19. arXiv:1710.05938. Bibcode:2017ApJ...850L..19M. doi:10.3847/2041-8213/aa991c.
37. Shibata, M.; Fujibayashi, S.; Hotokezaka, K.; Kiuchi, K.; Kyutoku, K.; Sekiguchi, Y.; Tanaka, M. (22 December 2017). "Modeling GW170817 based on numerical relativity and its implications". Physical Review D. 96 (12): 123012. arXiv:1710.07579. Bibcode:2017PhRvD..96l3012S. doi:10.1103/PhysRevD.96.123012.
38. Ruiz, M.; Shapiro, S. L.; Tsokaros, A. (11 January 2018). "GW170817, general relativistic magnetohydrodynamic simulations, and the neutron star maximum mass". Physical Review D. 97 (2): 021501. arXiv:1711.00473. Bibcode:2018PhRvD..97b1501R. doi:10.1103/PhysRevD.97.021501. PMC 6036631. PMID 30003183.
39. Rezzolla, L.; Most, E. R.; Weih, L. R. (9 January 2018). "Using Gravitational-wave Observations and Quasi-universal Relations to Constrain the Maximum Mass of Neutron Stars". Astrophysical Journal. 852 (2): L25. arXiv:1711.00314. Bibcode:2018ApJ...852L..25R. doi:10.3847/2041-8213/aaa401.
40. Ruffini, R.; Wheeler, J. A. (1971). "Introducing the black hole" (PDF). Physics Today. 24 (1): 30–41. Bibcode:1971PhT....24a..30R. doi:10.1063/1.3022513. Archived (PDF) from the original on 25 July 2011.CS1 maint: ref=harv (link)
41. Finkelstein, D. (1958). "Past-Future Asymmetry of the Gravitational Field of a Point Particle". Physical Review. 110 (4): 965–967. Bibcode:1958PhRv..110..965F. doi:10.1103/PhysRev.110.965.CS1 maint: ref=harv (link)
42. Kruskal, M. (1960). "Maximal Extension of Schwarzschild Metric". Physical Review. 119 (5): 1743. Bibcode:1960PhRv..119.1743K. doi:10.1103/PhysRev.119.1743.CS1 maint: ref=harv (link)
43. Hewish, A.; et al. (1968). "Observation of a Rapidly Pulsating Radio Source". Nature. 217 (5130): 709–713. Bibcode:1968Natur.217..709H. doi:10.1038/217709a0.CS1 maint: ref=harv (link)
44. Pilkington, J. D. H.; et al. (1968). "Observations of some further Pulsed Radio Sources". Nature. 218 (5137): 126–129. Bibcode:1968Natur.218..126P. doi:10.1038/218126a0.CS1 maint: ref=harv (link)
45. Hewish, A. (1970). "Pulsars". Annual Review of Astronomy and Astrophysics. 8 (1): 265–296. Bibcode:1970ARA&A...8..265H. doi:10.1146/annurev.aa.08.090170.001405.CS1 maint: ref=harv (link)
46. Newman, E. T.; et al. (1965). "Metric of a Rotating, Charged Mass". Journal of Mathematical Physics. 6 (6): 918. Bibcode:1965JMP.....6..918N. doi:10.1063/1.1704351.CS1 maint: ref=harv (link)
47. Israel, W. (1967). "Event Horizons in Static Vacuum Space-Times". Physical Review. 164 (5): 1776. Bibcode:1967PhRv..164.1776I. doi:10.1103/PhysRev.164.1776.CS1 maint: ref=harv (link)
48. Carter, B. (1971). "Axisymmetric Black Hole Has Only Two Degrees of Freedom". Physical Review Letters. 26 (6): 331. Bibcode:1971PhRvL..26..331C. doi:10.1103/PhysRevLett.26.331.CS1 maint: ref=harv (link)
49. Carter, B. (1977). "The vacuum black hole uniqueness theorem and its conceivable generalisations". Proceedings of the 1st Marcel Grossmann meeting on general relativity. pp. 243–254.
50. Robinson, D. (1975). "Uniqueness of the Kerr Black Hole". Physical Review Letters. 34 (14): 905. Bibcode:1975PhRvL..34..905R. doi:10.1103/PhysRevLett.34.905.CS1 maint: ref=harv (link)
51. Heusler, M. (2012). "Stationary Black Holes: Uniqueness and Beyond". Living Reviews in Relativity. 15 (7): 7. arXiv:1205.6112. Bibcode:2012LRR....15....7C. doi:10.12942/lrr-2012-7. PMC 5255892. PMID 28179837.CS1 maint: ref=harv (link)
52. Penrose, R. (1965). "Gravitational Collapse and Space-Time Singularities". Physical Review Letters. 14 (3): 57. Bibcode:1965PhRvL..14...57P. doi:10.1103/PhysRevLett.14.57.CS1 maint: ref=harv (link)
53. Ford, L. H. (2003). "The Classical Singularity Theorems and Their Quantum Loopholes". International Journal of Theoretical Physics. 42 (6): 1219–1227. arXiv:gr-qc/0301045. Bibcode:2003gr.qc.....1045F. doi:10.1023/A:1025754515197.CS1 maint: ref=harv (link)
54. Bardeen, J. M.; Carter, B.; Hawking, S. W. (1973). "The four laws of black hole mechanics". Communications in Mathematical Physics. 31 (2): 161–170. Bibcode:1973CMaPh..31..161B. doi:10.1007/BF01645742. MR 0334798. Zbl 1125.83309.CS1 maint: ref=harv (link)
55. Hawking, S. W. (1974). "Black hole explosions?". Nature. 248 (5443): 30–31. Bibcode:1974Natur.248...30H. doi:10.1038/248030a0.CS1 maint: ref=harv (link)
56. Popova, Maria (27 June 2016). "Mapping the Heavens: How Cosmology Shaped Our Understanding of the Universe and the Strange Story of How the Term "Black Hole" Was Born". brainpickings.org. Retrieved 12 April 2019.
57. "MIT's Marcia Bartusiak On Understanding Our Place In The Universe". www.wbur.org. Retrieved 12 April 2019.
58. Siegfried, Tom (23 December 2013). "50 years later, it's hard to say who named black holes". Science News. Archived from the original on 9 March 2017. Retrieved 24 September 2017. It seems that the "black hole" label was also bandied about in January 1964 in Cleveland at a meeting of the American Association for the Advancement of Science. Science News Letter reporter Ann Ewing reported from that meeting, describing how an intense gravitational field could cause a star to collapse in on itself. "Such a star then forms a 'black hole' in the universe," Ewing wrote
59. Brown, Emma (3 August 2010). "Ann E. Ewing, journalist first reported black holes". Boston.com. Archived from the original on 24 September 2017. Retrieved 24 September 2017.
60. "Pioneering Physicist John Wheeler Dies at 96". Scientific American. Archived from the original on 28 November 2016. Retrieved 27 November 2016.
61. Overbye, Dennis (14 April 2008). "John A. Wheeler, Physicist Who Coined the Term 'Black Hole,' Is Dead at 96". The New York Times. Archived from the original on 22 November 2016. Retrieved 27 November 2016.
62. Carroll 2004, p. 253
63. Thorne, K. S.; Price, R. H. (1986). Black holes: the membrane paradigm. Yale University Press. ISBN 978-0-300-03770-8.
64. Anderson, Warren G. (1996). "The Black Hole Information Loss Problem". Usenet Physics FAQ. Archived from the original on 22 January 2009. Retrieved 24 March 2009.
65. Preskill, J. (21 October 1994). Black holes and information: A crisis in quantum physics (PDF). Caltech Theory Seminar. Archived (PDF) from the original on 18 May 2008.
66. Hawking & Ellis 1973, Appendix B
67. Seeds, Michael A.; Backman, Dana E. (2007). Perspectives on Astronomy. Cengage Learning. p. 167. ISBN 978-0-495-11352-2. Archived from the original on 10 August 2016.CS1 maint: ref=harv (link)
68. Shapiro, S. L.; Teukolsky, S. A. (1983). Black holes, white dwarfs, and neutron stars: the physics of compact objects. John Wiley and Sons. p. 357. ISBN 978-0-471-87316-7.
69. Berger, B. K. (2002). "Numerical Approaches to Spacetime Singularities". Living Reviews in Relativity. 5 (1): 2002–1. arXiv:gr-qc/0201056. Bibcode:2002LRR.....5....1B. doi:10.12942/lrr-2002-1. PMC 5256073. PMID 28179859.CS1 maint: ref=harv (link)
70. McClintock, J. E.; Shafee, R.; Narayan, R.; Remillard, R. A.; Davis, S. W.; Li, L.-X. (2006). "The Spin of the Near-Extreme Kerr Black Hole GRS 1915+105". Astrophysical Journal. 652 (1): 518–539. arXiv:astro-ph/0606076. Bibcode:2006ApJ...652..518M. doi:10.1086/508457.CS1 maint: ref=harv (link)
71. Abbott, B. P.; et al. (LIGO Scientific Collaboration and Virgo Collaboration) (1 June 2017). "GW170104: Observation of a 50-Solar-Mass Binary Black Hole Coalescence at Redshift 0.2". Physical Review Letters. 118 (22): 221101. arXiv:1706.01812. Bibcode:2017PhRvL.118v1101A. doi:10.1103/PhysRevLett.118.221101. PMID 28621973.
72. Abbott, B. P.; et al. (LIGO Scientific Collaboration & Virgo Collaboration) (16 October 2017). "GW170817: Observation of Gravitational Waves from a Binary Neutron Star Inspiral". Physical Review Letters. 119 (16): 161101. arXiv:1710.05832. Bibcode:2017PhRvL.119p1101A. doi:10.1103/PhysRevLett.119.161101. PMID 29099225.
73. Wald 1984, pp. 124–125
74. Saa, Alberto; Santarelli, Raphael (18 July 2011). "Destroying a near-extremal Kerr–Newman black hole". Physical Review D. 84 (2): 027501. arXiv:1105.3950. Bibcode:2011PhRvD..84b7501S. doi:10.1103/PhysRevD.84.027501.
75. Misner, Thorne & Wheeler 1973, p. 848
76. Wheeler 2007, p. 179
77. Carroll 2004, Ch. 5.4 and 7.3
78. "Singularities and Black Holes > Lightcones and Causal Structure". plato.stanford.edu. Stanford Encyclopedia of Philosophy. Retrieved 11 March 2018.
79. Carroll 2004, p. 217
80. Carroll 2004, p. 218
81. "Inside a black hole". Knowing the universe and its secrets. Archived from the original on 23 April 2009. Retrieved 26 March 2009.
82. "What happens to you if you fall into a black holes". math.ucr.edu. John Baez. Retrieved 11 March 2018.
83. Carroll 2004, p. 222
84. "Watch: Three Ways an Astronaut Could Fall Into a Black Hole". 1 February 2014. Retrieved 13 March 2018.
85. Emparan, R.; Reall, H. S. (2008). "Black Holes in Higher Dimensions". Living Reviews in Relativity. 11 (6): 6. arXiv:0801.3471. Bibcode:2008LRR....11....6E. doi:10.12942/lrr-2008-6. PMC 5253845. PMID 28163607.CS1 maint: ref=harv (link)
86. Obers, N. A. (2009). Papantonopoulos, Eleftherios (ed.). Black Holes in Higher-Dimensional Gravity (PDF). Physics of Black Holes. Lecture Notes in Physics. 769. pp. 211–258. arXiv:0802.0519. Bibcode:2009LNP...769.....P. doi:10.1007/978-3-540-88460-6. ISBN 978-3-540-88459-0.CS1 maint: ref=harv (link)
87. Hawking & Ellis 1973, Ch. 9.3
88. Smarr, L. (1973). "Surface Geometry of Charged Rotating Black Holes". Physical Review D. 7 (2): 289–295. Bibcode:1973PhRvD...7..289S. doi:10.1103/PhysRevD.7.289.
89. Visser, M. (22 January 2009). "The Kerr spacetime: A brief introduction". In Wiltshire, D.L.; Visser, M.; Scott, S.M. (eds.). The Kerr Spacetime: Rotating Black Holes in General Relativity. Cambridge University Press. arXiv:0706.0622. ISBN 978-052188512-6.
90. Delgado, J.F. M.; Herdeiro, C.A. R.; Radu, E. (2018). "Horizon geometry for Kerr black holes with synchronized hair". Physical Review D. 97 (12): 124012. arXiv:1804.04910. Bibcode:2018PhRvD..97l4012D. doi:10.1103/PhysRevD.97.124012. hdl:10773/24121.
91. Carroll 2004, p. 205
92. Carroll 2004, pp. 264–265
93. Carroll 2004, p. 252
94. "Sizes of Black Holes? How Big is a Black Hole?". Sky & Telescope. 22 July 2014. Retrieved 9 October 2018.
95. Lewis, G. F.; Kwan, J. (2007). "No Way Back: Maximizing Survival Time Below the Schwarzschild Event Horizon". Publications of the Astronomical Society of Australia. 24 (2): 46–52. arXiv:0705.1029. Bibcode:2007PASA...24...46L. doi:10.1071/AS07012.CS1 maint: ref=harv (link)
96. Wheeler 2007, p. 182
97. Carroll 2004, pp. 257–259 and 265–266
98. Droz, S.; Israel, W.; Morsink, S. M. (1996). "Black holes: the inside story". Physics World. 9 (1): 34–37. Bibcode:1996PhyW....9...34D. doi:10.1088/2058-7058/9/1/26.CS1 maint: ref=harv (link)
99. Carroll 2004, p. 266
100. Poisson, E.; Israel, W. (1990). "Internal structure of black holes". Physical Review D. 41 (6): 1796–1809. Bibcode:1990PhRvD..41.1796P. doi:10.1103/PhysRevD.41.1796. PMID 10012548.CS1 maint: ref=harv (link)
101. Wald 1984, p. 212
102. Hamade, R. (1996). "Black Holes and Quantum Gravity". Cambridge Relativity and Cosmology. University of Cambridge. Archived from the original on 7 April 2009. Retrieved 26 March 2009.
103. Palmer, D. "Ask an Astrophysicist: Quantum Gravity and Black Holes". NASA. Archived from the original on 28 March 2009. Retrieved 26 March 2009.
104. Nitta, Daisuke; Chiba, Takeshi; Sugiyama, Naoshi (September 2011). "Shadows of colliding black holes". Physical Review D. 84 (6): 063008. arXiv:1106.2425. Bibcode:2011PhRvD..84f3008N. doi:10.1103/PhysRevD.84.063008.CS1 maint: ref=harv (link)
105. Visser, Matt (2007). "The Kerr spacetime: A brief introduction". page 35, Fig. 3. arXiv:0706.0622 [gr-qc].
106. Carroll 2004, Ch. 6.6
107. Carroll 2004, Ch. 6.7
108. Misner, Thorne & Wheeler 1973
109. Bardeen, J. M. (1972). "Rotating black holes: locally nonrotating frames, energy extraction, and scalar synchrotron radiation". The Astrophysical Journal. 178: 347–370. Bibcode:1972ApJ...178..347B. doi:10.1086/151796.
110. Einstein, A. (1939). "On A Stationary System With Spherical Symmetry Consisting of Many Gravitating Masses". Annals of Mathematics. 40 (4): 922–936. Bibcode:1939AnMat..40..922E. doi:10.2307/1968902. JSTOR 1968902.CS1 maint: ref=harv (link)
111. Kerr, R. P. (2009). "The Kerr and Kerr-Schild metrics". In Wiltshire, D. L.; Visser, M.; Scott, S. M. (eds.). The Kerr Spacetime. Cambridge University Press. arXiv:0706.1109. Bibcode:2007arXiv0706.1109K. ISBN 978-0-521-88512-6.
112. Hawking, S. W.; Penrose, R. (January 1970). "The Singularities of Gravitational Collapse and Cosmology". Proceedings of the Royal Society A. 314 (1519): 529–548. Bibcode:1970RSPSA.314..529H. doi:10.1098/rspa.1970.0021. JSTOR 2416467.CS1 maint: ref=harv (link)
113. Pacucci, F.; Ferrara, A.; Grazian, A.; Fiore, F.; Giallongo, E. (2016). "First Identification of Direct Collapse Black Hole Candidates in the Early Universe in CANDELS/GOODS-S". Mon. Not. R. Astron. Soc. 459 (2): 1432. arXiv:1603.08522. Bibcode:2016MNRAS.459.1432P. doi:10.1093/mnras/stw725.
114. Carr, B. J. (2005). "Primordial Black Holes: Do They Exist and Are They Useful?". In Suzuki, H.; Yokoyama, J.; Suto, Y.; Sato, K. (eds.). Inflating Horizon of Particle Astrophysics and Cosmology. Universal Academy Press. pp. astro–ph/0511743. arXiv:astro-ph/0511743. Bibcode:2005astro.ph.11743C. ISBN 978-4-946443-94-7.
115. Carroll 2004, Section 5.8
116. Griffiths, Martin (2012). Planetary Nebulae and How to Observe Them (illustrated ed.). Springer Science & Business Media. p. 11. ISBN 978-1-4614-1781-1. Archived from the original on 3 December 2016. Extract of page 11
117. "Artist's impression of supermassive black hole seed". Archived from the original on 30 May 2016. Retrieved 27 May 2016.
118. Rees, M. J.; Volonteri, M. (2007). Karas, V.; Matt, G. (eds.). Massive black holes: Formation and evolution. Proceedings of the International Astronomical Union. 238. pp. 51–58. arXiv:astro-ph/0701512. Bibcode:2007IAUS..238...51R. doi:10.1017/S1743921307004681. ISBN 978-0-521-86347-6.
119. Penrose, R. (2002). "Gravitational Collapse: The Role of General Relativity" (PDF). General Relativity and Gravitation. 34 (7): 1141. Bibcode:2002GReGr..34.1141P. doi:10.1023/A:1016578408204. Archived from the original (PDF) on 26 May 2013.CS1 maint: ref=harv (link)
120. Philip Gibbs. "Is the Big Bang a black hole?". John Baez. Retrieved 16 March 2018.
121. Giddings, S. B.; Thomas, S. (2002). "High energy colliders as black hole factories: The end of short distance physics". Physical Review D. 65 (5): 056010. arXiv:hep-ph/0106219. Bibcode:2002PhRvD..65e6010G. doi:10.1103/PhysRevD.65.056010.CS1 maint: ref=harv (link)
122. Harada, T. (2006). "Is there a black hole minimum mass?". Physical Review D. 74 (8): 084004. arXiv:gr-qc/0609055. Bibcode:2006PhRvD..74h4004H. doi:10.1103/PhysRevD.74.084004.CS1 maint: ref=harv (link)
123. Arkani–Hamed, N.; Dimopoulos, S.; Dvali, G. (1998). "The hierarchy problem and new dimensions at a millimeter". Physics Letters B. 429 (3–4): 263–272. arXiv:hep-ph/9803315. Bibcode:1998PhLB..429..263A. doi:10.1016/S0370-2693(98)00466-3.CS1 maint: ref=harv (link)
124. LHC Safety Assessment Group (2008). "Review of the Safety of LHC Collisions" (PDF). Journal of Physics G: Nuclear Physics. 35 (11): 115004. arXiv:0806.3414. Bibcode:2008JPhG...35k5004E. doi:10.1088/0954-3899/35/11/115004. Archived (PDF) from the original on 14 April 2010.
125. Cavaglià, M. (2010). "Particle accelerators as black hole factories?". Einstein-Online. 4: 1010. Archived from the original on 8 May 2013. Retrieved 8 May 2013.CS1 maint: ref=harv (link)
126. Vesperini, E.; McMillan, S. L. W.; d'Ercole, A.; et al. (2010). "Intermediate-Mass Black Holes in Early Globular Clusters". The Astrophysical Journal Letters. 713 (1): L41–L44. arXiv:1003.3470. Bibcode:2010ApJ...713L..41V. doi:10.1088/2041-8205/713/1/L41.CS1 maint: ref=harv (link)
127. Zwart, S. F. P.; Baumgardt, H.; Hut, P.; et al. (2004). "Formation of massive black holes through runaway collisions in dense young star clusters". Nature. 428 (6984): 724–726. arXiv:astro-ph/0402622. Bibcode:2004Natur.428..724P. doi:10.1038/nature02448. PMID 15085124.CS1 maint: ref=harv (link)
128. O'Leary, R. M.; Rasio, F. A.; Fregeau, J. M.; et al. (2006). "Binary Mergers and Growth of Black Holes in Dense Star Clusters". The Astrophysical Journal. 637 (2): 937–951. arXiv:astro-ph/0508224. Bibcode:2006ApJ...637..937O. doi:10.1086/498446.CS1 maint: ref=harv (link)
129. Page, D. N. (2005). "Hawking radiation and black hole thermodynamics". New Journal of Physics. 7 (1): 203. arXiv:hep-th/0409024. Bibcode:2005NJPh....7..203P. doi:10.1088/1367-2630/7/1/203.CS1 maint: ref=harv (link)
130. Carroll 2004, Ch. 9.6
131. Siegel, Ethan (2017). "Ask Ethan: Do Black Holes Grow Faster Than They Evaporate?". Forbes ("Starts With A Bang" blog). Retrieved 17 March 2018.
132. Sivaram, C. (2001). "Black hole Hawking radiation may never be observed!". General Relativity and Gravitation. 33 (2): 175–181. Bibcode:2001GReGr..33..175S. doi:10.1023/A:1002753400430.
133. "Evaporating black holes?". Einstein online. Max Planck Institute for Gravitational Physics. 2010. Archived from the original on 22 July 2011. Retrieved 12 December 2010.
134. Giddings, S. B.; Mangano, M. L. (2008). "Astrophysical implications of hypothetical stable TeV-scale black holes". Physical Review D. 78 (3): 035009. arXiv:0806.3381. Bibcode:2008PhRvD..78c5009G. doi:10.1103/PhysRevD.78.035009.CS1 maint: ref=harv (link)
135. Peskin, M. E. (2008). "The end of the world at the Large Hadron Collider?". Physics. 1: 14. Bibcode:2008PhyOJ...1...14P. doi:10.1103/Physics.1.14.CS1 maint: ref=harv (link)
136. Fichtel, C. E.; Bertsch, D. L.; Dingus, B. L.; et al. (1994). "Search of the energetic gamma-ray experiment telescope (EGRET) data for high-energy gamma-ray microsecond bursts". Astrophysical Journal. 434 (2): 557–559. Bibcode:1994ApJ...434..557F. doi:10.1086/174758.CS1 maint: ref=harv (link)
137. Naeye, R. "Testing Fundamental Physics". NASA. Archived from the original on 31 August 2008. Retrieved 16 September 2008.
138. Frautschi, S. (1982). "Entropy in an Expanding Universe". Science. 217 (4560): 593–599. Bibcode:1982Sci...217..593F. doi:10.1126/science.217.4560.593. PMID 17817517. See page 596: table 1 and section "black hole decay" and previous sentence on that page.
139. Page, Don N. (1976). "Particle emission rates from a black hole: Massless particles from an uncharged, nonrotating hole". Physical Review D. 13 (2): 198–206. Bibcode:1976PhRvD..13..198P. doi:10.1103/PhysRevD.13.198.. See in particular equation (27).
140. "Black Holes | Science Mission Directorate". NASA. Retrieved 17 March 2018.
141. "April 2017 Observations". Event Horizon Telescope. Retrieved 11 April 2019.
142. Overbye, Dennis (10 April 2019). "Darkness Visible, Finally: Astronomers Capture First Ever Image of a Black Hole". The New York Times. Retrieved 11 April 2019.
143. AP (10 April 2019). "Astronomers Reveal the First Picture of a Black Hole". The New York Times (video). Retrieved 11 April 2019.
144. Doeleman, Shep (4 April 2016). "The Event Horizon Telescope: Imaging and Time-Resolving a Black Hole". Physics @ Berkeley. Event occurs at 46:50. Archived from the original on 1 December 2016. Retrieved 8 July 2016.
145. Grossman, Lisa; Conover, Emily (10 April 2019). "The first picture of a black hole opens a new era of astrophysics". Science News. Retrieved 11 April 2019.
146. "The first picture of a black hole opens a new era of astrophysics". Science News. 10 April 2019. Retrieved 30 September 2019.
147. Johnson, M. D.; Fish, V. L.; Doeleman, S. S.; Marrone, D. P.; Plambeck, R. L.; Wardle, J. F. C.; Akiyama, K.; Asada, K.; Beaudoin, C. (4 December 2015). "Resolved magnetic-field structure and variability near the event horizon of Sagittarius A*". Science. 350 (6265): 1242–1245. arXiv:1512.01220. Bibcode:2015Sci...350.1242J. doi:10.1126/science.aac7087. PMID 26785487.
148. "Event Horizon Telescope Reveals Magnetic Fields at Milky Way's Central Black Hole". cfa.harvard.edu. 3 December 2015. Archived from the original on 31 December 2015. Retrieved 12 January 2016.
149. O. Straub, F.H. Vincent, M.A. Abramowicz, E. Gourgoulhon, T. Paumard, "Modelling the black hole silhouette in Sgr A* with ion tori", Astron. Astroph 543 (2012) A8
150. Overbye, Dennis (11 February 2016). "Physicists Detect Gravitational Waves, Proving Einstein Right". The New York Times. Archived from the original on 11 February 2016. Retrieved 11 February 2016.
151. Abbott, Benjamin P.; et al. (LIGO Scientific Collaboration & Virgo Collaboration) (11 February 2016). "Properties of the binary black hole merger GW150914". Physical Review Letters. 116 (24): 241102. arXiv:1602.03840. Bibcode:2016PhRvL.116x1102A. doi:10.1103/PhysRevLett.116.241102. PMID 27367378.
152. Cardoso, V.; Franzin, E.; Pani, P. (2016). "Is the gravitational-wave ringdown a probe of the event horizon?". Physical Review Letters. 116 (17): 171101. arXiv:1602.07309. Bibcode:2016PhRvL.116q1101C. doi:10.1103/PhysRevLett.116.171101. PMID 27176511.
153. Abbott, Benjamin P.; et al. (LIGO Scientific Collaboration & Virgo Collaboration) (11 February 2016). "Tests of general relativity with GW150914". LIGO. Archived from the original on 15 February 2016. Retrieved 12 February 2016.
154. Abbott, B. P.; et al. (LIGO Scientific Collaboration & Virgo Collaboration) (2016). "Astrophysical Implications of the Binary Black Hole Merger GW150914". Astrophys. J. Lett. 818 (2): L22. arXiv:1602.03846. Bibcode:2016ApJ...818L..22A. doi:10.3847/2041-8205/818/2/L22. Archived from the original on 16 March 2016.
155. Gillessen, S.; Eisenhauer, F.; Trippe, S.; et al. (2009). "Monitoring Stellar Orbits around the Massive Black Hole in the Galactic Center". The Astrophysical Journal. 692 (2): 1075–1109. arXiv:0810.4674. Bibcode:2009ApJ...692.1075G. doi:10.1088/0004-637X/692/2/1075.CS1 maint: ref=harv (link)
156. Ghez, A. M.; Klein, B. L.; Morris, M.; et al. (1998). "High Proper‐Motion Stars in the Vicinity of Sagittarius A*: Evidence for a Supermassive Black Hole at the Center of Our Galaxy". The Astrophysical Journal. 509 (2): 678–686. arXiv:astro-ph/9807210. Bibcode:1998ApJ...509..678G. doi:10.1086/306528.CS1 maint: ref=harv (link)
157. Broderick, Avery; Loeb, Abraham; Narayan, Ramesh (August 2009). "The Event Horizon of Sagittarius A*". The Astrophysical Journal. 701 (2): 1357–1366. arXiv:0903.1105. Bibcode:2009ApJ...701.1357B. doi:10.1088/0004-637X/701/2/1357.
158. "NASA's NuSTAR Sees Rare Blurring of Black Hole Light". NASA. 12 August 2014. Archived from the original on 13 August 2014. Retrieved 12 August 2014.
159. "Researchers clarify dynamics of black hole rotational energy". Retrieved 17 September 2018.
160. Marck, Jean-Alain (1 March 1996). "Short-cut method of solution of geodesic equations for Schwarzchild black hole". Classical and Quantum Gravity. 13 (3): 393–402. arXiv:gr-qc/9505010. Bibcode:1996CQGra..13..393M. doi:10.1088/0264-9381/13/3/007. ISSN 0264-9381.
161. McClintock, J. E.; Remillard, R. A. (2006). "Black Hole Binaries". In Lewin, W.; van der Klis, M. (eds.). Compact Stellar X-ray Sources. p. 157. arXiv:astro-ph/0306213. Bibcode:2006csxs.book..157M. ISBN 978-0-521-82659-4. section 4.1.5.
162. "What powers a black hole's mighty jets?". Science | AAAS. 19 November 2014. Retrieved 19 March 2018.
163. Celotti, A.; Miller, J. C.; Sciama, D. W. (1999). "Astrophysical evidence for the existence of black holes" (PDF). Classical and Quantum Gravity. 16 (12A): A3–A21. arXiv:astro-ph/9912186. Bibcode:1999CQGra..16A...3C. doi:10.1088/0264-9381/16/12A/301.CS1 maint: ref=harv (link)
164. Winter, L. M.; Mushotzky, R. F.; Reynolds, C. S. (2006). "XMM‐Newton Archival Study of the Ultraluminous X‐Ray Population in Nearby Galaxies". The Astrophysical Journal. 649 (2): 730–752. arXiv:astro-ph/0512480. Bibcode:2006ApJ...649..730W. doi:10.1086/506579.CS1 maint: ref=harv (link)
165. [e-mail]. "Hubble directly observes the disk around a black hole". www.spacetelescope.org -GB. Archived from the original on 8 March 2016. Retrieved 7 March 2016.
166. Muñoz, José A.; Mediavilla, Evencio; Kochanek, Christopher S.; Falco, Emilio; Mosquera, Ana María (1 December 2011). "A Study of Gravitational Lens Chromaticity with the Hubble Space Telescope". The Astrophysical Journal. 742 (2): 67. arXiv:1107.5932. Bibcode:2011ApJ...742...67M. doi:10.1088/0004-637X/742/2/67.
167. Bolton, C. T. (1972). "Identification of Cygnus X-1 with HDE 226868". Nature. 235 (5336): 271–273. Bibcode:1972Natur.235..271B. doi:10.1038/235271b0.CS1 maint: ref=harv (link)
168. Webster, B. L.; Murdin, P. (1972). "Cygnus X-1 – a Spectroscopic Binary with a Heavy Companion ?". Nature. 235 (5332): 37–38. Bibcode:1972Natur.235...37W. doi:10.1038/235037a0.CS1 maint: ref=harv (link)
169. Rolston, B. (10 November 1997). "The First Black Hole". The bulletin. University of Toronto. Archived from the original on 2 May 2008. Retrieved 11 March 2008.
170. Shipman, H. L.; Yu, Z; Du, Y.W (1 January 1975). "The implausible history of triple star models for Cygnus X-1 Evidence for a black hole". Astrophysical Letters. 16 (1): 9–12. Bibcode:1975ApL....16....9S. doi:10.1016/S0304-8853(99)00384-4.CS1 maint: ref=harv (link)
171. "NASA scientists identify smallest known black hole" (Press release). Goddard Space Flight Center. 1 April 2008. Archived from the original on 27 December 2008. Retrieved 14 March 2009.
172. Krolik, J. H. (1999). Active Galactic Nuclei. Princeton University Press. Ch. 1.2. ISBN 978-0-691-01151-6.
173. Sparke, L. S.; Gallagher, J. S. (2000). Galaxies in the Universe: An Introduction. Cambridge University Press. Ch. 9.1. ISBN 978-0-521-59740-1.
174. Chou, Felicia; Anderson, Janet; Watzke, Megan (5 January 2015). "RELEASE 15-001 – NASA's Chandra Detects Record-Breaking Outburst from Milky Way's Black Hole". NASA. Archived from the original on 6 January 2015. Retrieved 6 January 2015.
175. Kormendy, J.; Richstone, D. (1995). "Inward Bound – The Search For Supermassive Black Holes In Galactic Nuclei". Annual Review of Astronomy and Astrophysics. 33 (1): 581–624. Bibcode:1995ARA&A..33..581K. doi:10.1146/annurev.aa.33.090195.003053.CS1 maint: ref=harv (link)
176. King, A. (2003). "Black Holes, Galaxy Formation, and the MBH-σ Relation". The Astrophysical Journal Letters. 596 (1): 27–29. arXiv:astro-ph/0308342. Bibcode:2003ApJ...596L..27K. doi:10.1086/379143.CS1 maint: ref=harv (link)
177. Ferrarese, L.; Merritt, D. (2000). "A Fundamental Relation Between Supermassive Black Holes and their Host Galaxies". The Astrophysical Journal Letters. 539 (1): 9–12. arXiv:astro-ph/0006053. Bibcode:2000ApJ...539L...9F. doi:10.1086/312838.CS1 maint: ref=harv (link)
178. "A Black Hole's Dinner is Fast Approaching". ESO Press Release. Archived from the original on 13 February 2012. Retrieved 6 February 2012.
179. Bozza, V. (2010). "Gravitational Lensing by Black Holes". General Relativity and Gravitation. 42 (9): 2269–2300. arXiv:0911.2187. Bibcode:2010GReGr..42.2269B. doi:10.1007/s10714-010-0988-2.CS1 maint: ref=harv (link)
180. Kovacs, Z.; Cheng, K. S.; Harko, T. (2009). "Can stellar mass black holes be quark stars?". Monthly Notices of the Royal Astronomical Society. 400 (3): 1632–1642. arXiv:0908.2672. Bibcode:2009MNRAS.400.1632K. doi:10.1111/j.1365-2966.2009.15571.x.CS1 maint: ref=harv (link)
181. Kusenko, A. (2006). "Properties and signatures of supersymmetric Q-balls". arXiv:hep-ph/0612159.
182. Hansson, J.; Sandin, F. (2005). "Preon stars: a new class of cosmic compact objects". Physics Letters B. 616 (1–2): 1–7. arXiv:astro-ph/0410417. Bibcode:2005PhLB..616....1H. doi:10.1016/j.physletb.2005.04.034.CS1 maint: ref=harv (link)
183. Kiefer, C. (2006). "Quantum gravity: general introduction and recent developments". Annalen der Physik. 15 (1–2): 129–148. arXiv:gr-qc/0508120. Bibcode:2006AnP...518..129K. doi:10.1002/andp.200510175.CS1 maint: ref=harv (link)
184. Skenderis, K.; Taylor, M. (2008). "The fuzzball proposal for black holes". Physics Reports. 467 (4–5): 117. arXiv:0804.0552. Bibcode:2008PhR...467..117S. doi:10.1016/j.physrep.2008.08.001.CS1 maint: ref=harv (link)
185. Choi, Charles Q. (2018). "Black Hole Pretenders Could Really Be Bizarre Quantum Stars". Scientific American. Retrieved 17 March 2018.
186. Ball, Philip (31 March 2005). "Black holes 'do not exist'". Nature. doi:10.1038/news050328-8.
187. Hawking, S. W. (1971). "Gravitational Radiation from Colliding Black Holes". Physical Review Letters. 26 (21): 1344–1346. Bibcode:1971PhRvL..26.1344H. doi:10.1103/PhysRevLett.26.1344.CS1 maint: ref=harv (link)
188. Wald, R. M. (2001). "The Thermodynamics of Black Holes". Living Reviews in Relativity. 4 (1): 6. arXiv:gr-qc/9912119. Bibcode:2001LRR.....4....6W. doi:10.12942/lrr-2001-6. PMC 5253844. PMID 28163633.CS1 maint: ref=harv (link)
189. 't Hooft, G. (2001). "The Holographic Principle". In Zichichi, A. (ed.). Basics and Highlights in Fundamental Physics. Basics and Highlights in Fundamental Physics. Subnuclear series. 37. pp. 72–100. arXiv:hep-th/0003004. Bibcode:2001bhfp.conf...72T. doi:10.1142/9789812811585_0005. ISBN 978-981-02-4536-8.
190. Strominger, A.; Vafa, C. (1996). "Microscopic origin of the Bekenstein-Hawking entropy". Physics Letters B. 379 (1–4): 99–104. arXiv:hep-th/9601029. Bibcode:1996PhLB..379...99S. doi:10.1016/0370-2693(96)00345-0.CS1 maint: ref=harv (link)
191. Carlip, S. (2009). "Black Hole Thermodynamics and Statistical Mechanics". Physics of Black Holes. Physics of Black Holes. Lecture Notes in Physics. 769. pp. 89–123. arXiv:0807.4520. Bibcode:2009LNP...769...89C. doi:10.1007/978-3-540-88460-6_3. ISBN 978-3-540-88459-0.CS1 maint: ref=harv (link)
192. Hawking, S. W. "Does God Play Dice?". www.hawking.org.uk. Archived from the original on 11 January 2012. Retrieved 14 March 2009.
193. Giddings, S. B. (1995). "The black hole information paradox". Particles, Strings and Cosmology. Johns Hopkins Workshop on Current Problems in Particle Theory 19 and the PASCOS Interdisciplinary Symposium 5. arXiv:hep-th/9508151. Bibcode:1995hep.th....8151G.
194. Unruh, William G.; Wald, Robert M. (2017). "Information loss". Reports on Progress in Physics. 80 (9): 092002. arXiv:1703.02140. Bibcode:2017RPPh...80i2002U. doi:10.1088/1361-6633/aa778e. PMID 28585922.
195. Mathur, S. D. (2011). The information paradox: conflicts and resolutions. XXV International Symposium on Lepton Photon Interactions at High Energies. arXiv:1201.2079. Bibcode:2012Prama..79.1059M. doi:10.1007/s12043-012-0417-z.
196. Page, Don N. (1993). "Information in black hole radiation". Phys. Rev. Lett. 71 (23): 3743–3746. arXiv:hep-th/9306083. Bibcode:1993PhRvL..71.3743P. CiteSeerX 10.1.1.267.174. doi:10.1103/PhysRevLett.71.3743. PMID 10055062.
197. Page, Don N. (1993). "Average entropy of a subsystem". Phys. Rev. Lett. 71 (9): 1291–1294. arXiv:gr-qc/9305007. Bibcode:1993PhRvL..71.1291P. CiteSeerX 10.1.1.339.7694. doi:10.1103/PhysRevLett.71.1291. PMID 10055503.
198. Merali, Zeeya (3 April 2013). "Astrophysics: Fire in the hole!". Nature. 496 (7443): 20–23. Bibcode:2013Natur.496...20M. doi:10.1038/496020a. PMID 23552926.
199. Ouellette, Jennifer (21 December 2012). "Black Hole Firewalls Confound Theoretical Physicists". Scientific American. Archived from the original on 9 November 2013. Retrieved 29 October 2013. Originally published Archived 3 June 2014 at the Wayback Machine in Quanta Magazine, 21 December 2012.

Further reading

Popular reading

• Ferguson, Kitty (1991). Black Holes in Space-Time. Watts Franklin. ISBN 978-0-531-12524-3.CS1 maint: ref=harv (link)
• Hawking, Stephen (1988). A Brief History of Time. Bantam Books, Inc. ISBN 978-0-553-38016-3.CS1 maint: ref=harv (link)
• Hawking, Stephen; Penrose, Roger (1996). The Nature of Space and Time. Princeton University Press. ISBN 978-0-691-03791-2.CS1 maint: ref=harv (link)
• Melia, Fulvio (2003). The Black Hole at the Center of Our Galaxy. Princeton U Press. ISBN 978-0-691-09505-9.CS1 maint: ref=harv (link)
• Melia, Fulvio (2003). The Edge of Infinity. Supermassive Black Holes in the Universe. Cambridge U Press. ISBN 978-0-521-81405-8.CS1 maint: ref=harv (link)
• Pickover, Clifford (1998). Black Holes: A Traveler's Guide. Wiley, John & Sons, Inc. ISBN 978-0-471-19704-1.
• Thorne, Kip S. (1994). Black Holes and Time Warps. Norton, W. W. & Company, Inc. ISBN 978-0-393-31276-8.CS1 maint: ref=harv (link)
• Susskind, Leonard (2008). The Black Hole War: My Battle with Stephen Hawking to Make the World Safe for Quantum Mechanics. Little, Brown and Company. ISBN 978-0316016407.CS1 maint: ref=harv (link)
• Wheeler, J. Craig (2007). Cosmic Catastrophes (2nd ed.). Cambridge University Press. ISBN 978-0-521-85714-7.CS1 maint: ref=harv (link)

University textbooks and monographs

• Carroll, Sean M. (2004). Spacetime and Geometry. Addison Wesley. ISBN 978-0-8053-8732-2.CS1 maint: ref=harv (link), the lecture notes on which the book was based are available for free from Sean Carroll's website.
• Carter, B. (1973). "Black hole equilibrium states". In DeWitt, B. S.; DeWitt, C. (eds.). Black Holes.CS1 maint: ref=harv (link)
• Chandrasekhar, Subrahmanyan (1999). Mathematical Theory of Black Holes. Oxford University Press. ISBN 978-0-19-850370-5.CS1 maint: ref=harv (link)
• Frolov, V. P.; Novikov, I. D. (1998). "Black hole physics". Cite journal requires |journal= (help)CS1 maint: ref=harv (link)
• Frolov, Valeri P.; Zelnikov, Andrei (2011). Introduction to Black Hole Physics. Oxford: Oxford University Press. ISBN 978-0-19-969229-3. Zbl 1234.83001.CS1 maint: ref=harv (link)
• Hawking, S. W.; Ellis, G. F. R. (1973). Large Scale Structure of space time. Cambridge University Press. ISBN 978-0-521-09906-6.CS1 maint: ref=harv (link)
• Melia, Fulvio (2007). The Galactic Supermassive Black Hole. Princeton U Press. ISBN 978-0-691-13129-0.CS1 maint: ref=harv (link)
• Misner, Charles; Thorne, Kip S.; Wheeler, John (1973). Gravitation. W. H. Freeman and Company. ISBN 978-0-7167-0344-0.CS1 maint: ref=harv (link)
• Taylor, Edwin F.; Wheeler, John Archibald (2000). Exploring Black Holes. Addison Wesley Longman. ISBN 978-0-201-38423-9.CS1 maint: ref=harv (link)
• Wald, Robert M. (1984). General Relativity. University of Chicago Press. ISBN 978-0-226-87033-5.CS1 maint: ref=harv (link)
• Wald, Robert M. (1992). Space, Time, and Gravity: The Theory of the Big Bang and Black Holes. University of Chicago Press. ISBN 978-0-226-87029-8.CS1 maint: ref=harv (link)
• Price, Richard; Creighton, Teviet (2008). "Black holes". Scholarpedia. 3 (1): 4277. Bibcode:2008SchpJ...3.4277C. doi:10.4249/scholarpedia.4277.

Review papers

• Gallo, Elena; Marolf, Donald (2009). "Resource Letter BH-2: Black Holes". American Journal of Physics. 77 (4): 294–307. arXiv:0806.2316. Bibcode:2009AmJPh..77..294G. doi:10.1119/1.3056569.CS1 maint: ref=harv (link)
• Hughes, Scott A. (2005). "Trust but verify: The case for astrophysical black holes". arXiv:hep-ph/0511217. Lecture notes from 2005 SLAC Summer Institute.

External links

• Black Holes on In Our Time at the BBC
• Stanford Encyclopedia of Philosophy: "Singularities and Black Holes" by Erik Curiel and Peter Bokulich.
• Black Holes: Gravity's Relentless Pull – Interactive multimedia Web site about the physics and astronomy of black holes from the Space Telescope Science Institute
• ESA's Black Hole Visualization
• Frequently Asked Questions (FAQs) on Black Holes
• "Schwarzschild Geometry"
• Hubble site

Videos

• 16-year-long study tracks stars orbiting Milky Way black hole
• Movie of Black Hole Candidate from Max Planck Institute
• Cowen, Ron (20 April 2015). "3D simulations of colliding black holes hailed as most realistic yet". Nature. doi:10.1038/nature.2015.17360.
• Computer visualisation of the signal detected by LIGO
• Two Black Holes Merge into One (based upon the signal GW150914)