Xcas
Xcas is a user interface to Giac, a free,[1] open source[2] basic Computer Algebra System (CAS)[3] for Microsoft Windows, Apple macOS (only 32 bit version) and Linux/Unix;[4] Xcas is written in C++.[5] Giac can be used directly inside software written in C++.
 | |
| Developer(s) | Bernard Parisse |
|---|---|
| Initial release | 2000 |
| Stable release | 1.5.0-85
/ 12 December 2019 |
| Repository | |
| Written in | C++ |
| Operating system | Windows, macOS, Linux |
| Type | Computer algebra system |
| License | GNU GPL |
| Website | www-fourier |
Giac has a compatibility mode with WolframAlpha,[6] Mathematica, Maple,[7] MuPAD, Matlab, Yacas, SageMath, Qcas, ExpressionsinBar (64 bit app for macOS)[8][9] and Magma, CPMP-Tools, WordMat (addon to Microsoft Word)[10] software and TI-89, TI-92, Voyage 200 and TI-Nspire calculators.[11] Users can use Giac/Xcas as well as a free software compatible with Maple to develop formal algorithms or use it in other software. Xcas is used in SageMath for calculus operations. Among other things Xcas can solve equations and draw graphs. There is a forum for questions about Xcas.[12]
CmathOOoCAS, an OpenOffice.org plugin which allows formal calculation in Calc spreadsheet and Writer word processing, uses Xcas to perform calculations.
Features
Here is a brief overview of what Xcas is able to do:[13]
- Xcas has the ability of a scientific calculator that provides show input and writes pretty print
- Xcas works also as a spreadsheet;[14]
- computer algebra;
- 2D geometry in the plane;[15]
- 3D geometry in space;[15]
- spreadsheet;[14]
- statistics;
- regression (exponential, linear, logaritmic, logistic, polynomial, power)
- programming;[16]
- solve equations even with complex roots;
- solving trigonometric equations
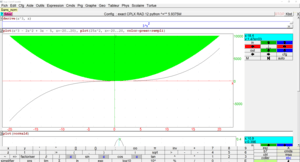
- solve differential equations[17][18] (watch illustration);
- draw graphs;
- calculate differential (or derivative) of functions;
- calculate antiderivative of functions;
- calculate area and integral calculus;
- linear algebra[19]
Some Xcas commands
- propfrac(42/15) = 2 + 4/5
- Calculate square root = sqrt(4) = 2
- Draw a vertical line in coordinate system: line(x=1) = the vertical line x=1
- Draw graph: plot(function)
- Calculate average: mean([3, 4, 2]) = 3
- Calculate variance: variance([3, 4, 2]) = 2/3
- Calculate standard deviation: stddev([3, 4, 2]) = sqrt(2/3)
- Calculate determinant of a matrix: det([[1,2], [3,4]]) = -2
- Calculate local extrema of a function: extrema(-2*cos(x)-cos(x)^2, x) = [0], [pi]
- Calculate cross product of two vectors: cross([1, 2, 3], [4, 3, 2]) = [-5, 10, -5]
- Calculate permutations: nPr()
- Calculate combinations: nCr()
- Solve equation: solve(equation,x)
- Factoring Polynomial: factor(polynomial,x) or cfactor(polynomial,x)
- Differentiation of function: diff(function,x)
- Calculate integral aka antiderivative: int(function,x)
- Calculate definite integral aka area under curve: int(function,x,lowerlimit,upperlimit)
- Calculate definite integral aka solid of revolution - finding volume by rotation (around the x axis): int(pi*function^2,x,lowerlimit,upperlimit)
- Calculate definite integral aka Solid of Revolution - finding volume by rotation (around the y axis) for a decreasing function: int(2*pi*x*function,x,lowerlimit,upperlimit)
- Separation of variables: split((x+1)*(y-2),[x,y]) = [x+1,y-2]
- desolve differential equation (right side of Differential Equation written as y’ or y’’): desolve(differential equation,y)
Read more commands and features here: http://www-fourier.ujf-grenoble.fr/~parisse/giac/cascmd_en.pdf
Xcas works for these operation Systems
History
Xcas and Giac are open-source projects [23] developed by Bernard Parisse[24] et al. at the Joseph Fourier University of Grenoble (Isère), France, since 2000.[5] Xcas and Giac are based on experiences gained with Parisse's former project Erable.[25] In 2013 the mathematical software Xcas was also integrated into GeoGebra's CAS view.[26] Since 2013 there are videos showing how Xcas works.[23][27]
Pocket CAS and CAS Calc P11 utilize Giac.
The system was also chosen by Hewlett-Packard as the CAS for their HP Prime calculator, which utilizes the Giac/Xcas 1.4.9 engine under a dual-license scheme.
See also
- Comparison of computer algebra systems
References
- "Berkeley Madonna alternatives". getalternative.net. Retrieved 2020-04-20.
- "COMPARISON OF OPEN SOURCE SOFTWARES IN MATHEMATICS EDUCATION". Konuralp Journal of Mathematics. 2019-05-02. Retrieved 2016-03-02.
- "Computer algebra in gravity research". University of Mons. 2019-05-05. Retrieved 2018-05-12.
- "Freeware and Open Source Software Tools for Distance Learning in Mathematics". University of Mons. 2019-05-05. Retrieved 2015-07-16.
- "Development of a user–friendly and open–source multibody framework with the help of symbolic tools". University of Mons. 2019-05-05. Retrieved 2011-06-01.
- "Differences between Expected Answers and the Answers Offered by Computer Algebra Systems to School Mathematics Equations" (PDF).
- "xcas - Computer Algebra System - console and graphical calculator". reposcope.com. Retrieved 2020-04-12.
- "ExpressionsinBar". www.alelvisoftware.com. Retrieved 2020-03-27.
- "ExpressionsinBar".
- "WordMat". Microsoft WordMat. Retrieved 2020-03-27.
- https://swmath.org/software/6662
- "Le forum de XCAS - Page d'accueil". xcas.univ-grenoble-alpes.fr. Retrieved 2020-04-12.
- "MATHEMATICS EDUCATION AS A SCIENCE AND A PROFESSION" (PDF). Josip Juraj Strossmayer University of Osijek. 2019-05-02. Retrieved 2017-10-05.
- https://www.yumpu.com/en/document/read/21966726/xcas-reference-card
- http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.580.4878&rep=rep1&type=pdf
- "Using Xcas in Calculus Curricula: a Plan of Lectures and Laboratory Projects" (PDF). Computational and Applied Mathematics Journal. 2019-11-15. Retrieved 2015-10-03.
- Halkos, George E.; Tsilika, Kyriaki D. (2011). "Xcas as a Programming Environment for Stability Conditions for a Class of Differential Equation Models in Economics". American Institute of Physics Conference Series. 1389 (1): 1769. Bibcode:2011AIPC.1389.1769H. doi:10.1063/1.3636951.
- "Integration and Differential Equations".
- "Computeralgebra-Rundbrief Nr. 62: Fachgruppe Computeralgebra" (PDF). (Gesellschaft fuer Informatik e.V. 2019-05-02. Retrieved 2018-03-02. (in German)
- "Xcas for Windows". logitheque. 2016-06-09. Retrieved 2018-12-05.
- "Symbolic Algebra Everywhere". Joey Bernard. 2015-12-15. Retrieved 2018-12-05.
- https://www.scribd.com/document/363002275/Xcas-Calcul-Formel-Lycee
- https://www.hpmuseum.org/forum/thread-9977.html
- "Bernard Parisse - "GIAC/XCAS and PARI/GP"".
- "Computer algebra in gravity research". University of Mons. 2019-05-05. Retrieved 2018-12-05.
- "Xcas". SemanticScholar. 2016-06-09. Retrieved 2018-12-05.
- "Bernard Parisse - "GIAC/XCAS and PARI/GP"".
Further reading
- De Graeve, Renée (2018-01-19) [2013]. "Symbolic computation and Mathematics with the calculator HP Prime" (PDF). Translated by Lecointre, Jean Michel. Retrieved 2018-01-22.
- Halkos, George (2015-04-25) [2014]. "Perspectives on integrating a computer algebra system into advanced calculus curricula" (PDF). Retrieved 2019-09-06.
- Read more commands here: http://www-fourier.ujf-grenoble.fr/~parisse/giac/cascmd_en.pdf
- http://www.mathsaulycee.sitew.com/fs/premiere_s/8uoow-xcas_commande_utile.pdf (French)
- http://briand-lyc.spip.ac-rouen.fr/IMG/pdf/xcas_fonctions.pdf (French)
- Barnard Parisse: Mathématiques avec Xcas. (French)
- Dr. Fabian Reimers (editor): "Computeralgebra-Rundbrief Nr. 62: Fachgruppe Computeralgebra" (PDF). (German)