SymPy

SymPy is an open-source Python library for symbolic computation. It provides computer algebra capabilities either as a standalone application, as a library to other applications, or live on the web as SymPy Live or SymPy Gamma. SymPy is simple to install and to inspect because it is written entirely in Python with few dependencies.[2][3][4] This ease of access combined with a simple and extensible code base in a well known language make SymPy a computer algebra system with a relatively low barrier to entry.

Not to be confused with SimPy, a discrete-event simulation language.
SymPy
Developer(s)SymPy Development Team
Initial release2007 (2007)
Stable release
1.6.2[1] / 9 August 2020 (2020-08-09)
Repository
Written inPython
Operating systemCross-platform
TypeComputer algebra system
LicenseNew BSD License
Websitewww.sympy.org/ 

SymPy includes features ranging from basic symbolic arithmetic to calculus, algebra, discrete mathematics and quantum physics. It is capable of formatting the result of the computations as LaTeX code.[2][3]

SymPy is free software and is licensed under New BSD License. The lead developers are Ondřej Čertík and Aaron Meurer. It was started in 2005 by Ondřej Čertík.[5]

Features

The SymPy library is split into a core with many optional modules.

Currently, the core of SymPy has around 260,000 lines of code[6] (also includes a comprehensive set of self-tests: over 100,000 lines in 350 files as of version 0.7.5), and its capabilities include:[2][3][7][8][9]

Core capabilities
  • Basic arithmetic: *, /, +, -, **
  • Simplification
  • Expansion
  • Functions: trigonometric, hyperbolic, exponential, roots, logarithms, absolute value, spherical harmonics, factorials and gamma functions, zeta functions, polynomials, hypergeometric, special functions, ...
  • Substitution
  • Arbitrary precision integers, rationals and floats
  • Noncommutative symbols
  • Pattern matching

Polynomials

Calculus

Solving equations

Discrete math

Matrices

Geometry
  • Points, lines, rays, segments, ellipses, circles, polygons, ...
  • Intersections
  • Tangency
  • Similarity

Plotting

Note, plotting requires the external matplotlib or Pyglet module.

  • Coordinate models
  • Plotting Geometric Entities
  • 2D and 3D
  • Interactive interface
  • Colors
  • Animations

Physics

Statistics

Combinatorics

Printing

Dependencies

Since version 1.0, SymPy has the mpmath package as a dependency.

There are several optional dependencies that can enhance its capabilities:

  • gmpy: If gmpy is installed, the SymPy's polynomial module will automatically use it for faster ground types. This can provide a several times boost in performance of certain operations.
  • matplotlib: If matplotlib is installed, SymPy can use it for plotting.
  • Pyglet: Alternative plotting package.

Usage examples

Pretty-printing

Sympy allows outputs to be formatted into a more appealing format through the pprint function. Alternatively, the init_printing() method will enable pretty-printing, so pprint need not be called. Pretty-printing will use unicode symbols when available in the current environment, otherwise it will fall back to ASCII characters.

>>> from sympy import pprint, init_printing, Symbol, sin, cos, exp, sqrt, series, Integral, Function
>>>
>>> x = Symbol("x")
>>> y = Symbol("y")
>>> f = Function('f')
>>> # pprint will default to unicode if available
>>> pprint( x**exp(x) )
 ⎛ x⎞
 ⎝ℯ ⎠
x   
>>> # An output without unicode
>>> pprint(Integral(f(x), x), use_unicode=False)
  /       
 |        
 | f(x) dx
 |        
/        
>>> # Compare with same expression but this time unicode is enabled
>>> pprint(Integral(f(x), x), use_unicode=True)
⌠        
⎮ f(x) dx
⌡     
>>> # Alternatively, you can call init_printing() once and pretty-print without the pprint function.
>>> init_printing()
>>> sqrt(sqrt(exp(x)))
   ____
4 ╱  x 
╲╱  ℯ  
>>> (1/cos(x)).series(x, 0, 10)
     2      4       6        8         
    x    5⋅x    61⋅x    277⋅x     ⎛ 10⎞
1 + ── + ──── + ───── + ────── + O⎝x  ⎠
    2     24     720     8064

Expansion

 
>>> from sympy import init_printing, Symbol, expand
>>> init_printing()
>>>
>>> a = Symbol('a')
>>> b = Symbol('b')
>>> e = (a + b)**5
>>> e
       5
(a + b) 
>>> e.expand()
 5     4        3  2      2  3       4    5
a  + 5⋅a ⋅b + 10⋅a ⋅b  + 10⋅a ⋅b  + 5⋅a⋅b  + b

Arbitrary-precision example

 
>>> from sympy import Rational, pprint
>>> e = 2**50 / Rational(10)**50
>>> pprint(e)
1/88817841970012523233890533447265625

Differentiation

 
>>> from sympy import init_printing, symbols, ln, diff
>>> init_printing()
>>> x, y = symbols('x y')
>>> f = x**2 / y + 2 * x - ln(y)
>>> diff(f, x)
 2⋅x    
 ─── + 2
  y 
>>> diff(f, y)
    2    
   x    1
 - ── - ─
    2   y
   y
>>> diff(diff(f, x), y)
 -2⋅x
 ────
   2 
  y

Plotting
Output of the plotting example
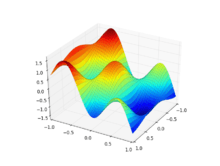
>>> from sympy import symbols, cos
>>> from sympy.plotting import plot3d
>>> x, y = symbols('x y')
>>> plot3d(cos(x*3)*cos(y*5)-y, (x, -1, 1), (y, -1, 1))
<sympy.plotting.plot.Plot object at 0x3b6d0d0>

Limits

 
>>> from sympy import init_printing, Symbol, limit, sqrt, oo
>>> init_printing()
>>> 
>>> x = Symbol('x')
>>> limit(sqrt(x**2 - 5*x + 6) - x, x, oo)
-5/2
>>> limit(x*(sqrt(x**2 + 1) - x), x, oo)
1/2
>>> limit(1/x**2, x, 0)
∞
>>> limit(((x - 1)/(x + 1))**x, x, oo)
 -2
ℯ

Differential equations

 
>>> from sympy import init_printing, Symbol, Function, Eq, dsolve, sin, diff
>>> init_printing()
>>>
>>> x = Symbol("x")
>>> f = Function("f")
>>>
>>> eq = Eq(f(x).diff(x), f(x))
>>> eq
d              
──(f(x)) = f(x)
dx         
>>>    
>>> dsolve(eq, f(x))
           x
f(x) = C₁⋅ℯ

>>>
>>> eq = Eq(x**2*f(x).diff(x), -3*x*f(x) + sin(x)/x)
>>> eq
 2 d                      sin(x)
x ⋅──(f(x)) = -3⋅x⋅f(x) + ──────
   dx                       x   
>>>
>>> dsolve(eq, f(x))
       C₁ - cos(x)
f(x) = ───────────
             3    
            x

Integration

 
>>> from sympy import init_printing, integrate, Symbol, exp, cos, erf
>>> init_printing()
>>> x = Symbol('x')
>>> # Polynomial Function
>>> f = x**2 + x + 1
>>> f
 2        
x  + x + 1
>>> integrate(f,x)
 3    2    
x    x     
── + ── + x
3    2     
>>> # Rational Function
>>> f = x/(x**2+2*x+1)
>>> f
     x      
────────────
 2          
x  + 2⋅x + 1

>>> integrate(f, x)
               1  
log(x + 1) + ─────
             x + 1
>>> # Exponential-polynomial functions
>>> f = x**2 * exp(x) * cos(x)
>>> f
 2  x       
x ⋅ℯ ⋅cos(x)
>>> integrate(f, x)
 2  x           2  x                         x           x       
x ⋅ℯ ⋅sin(x)   x ⋅ℯ ⋅cos(x)      x          ℯ ⋅sin(x)   ℯ ⋅cos(x)
──────────── + ──────────── - x⋅ℯ ⋅sin(x) + ───────── - ─────────
     2              2                           2           2    
>>> # A non-elementary integral
>>> f = exp(-x**2) * erf(x)
>>> f
   2       
 -x        
ℯ   ⋅erf(x)
>>> integrate(f, x)

  ___    2   
╲╱ π ⋅erf (x)
─────────────
      4

Series

 
>>> from sympy import Symbol, cos, sin, pprint
>>> x = Symbol('x')
>>> e = 1/cos(x)
>>> pprint(e)
  1   
──────
cos(x)
>>> pprint(e.series(x, 0, 10))
     2      4       6        8         
    x    5⋅x    61⋅x    277⋅x     ⎛ 10⎞
1 + ── + ──── + ───── + ────── + O⎝x  ⎠
    2     24     720     8064          
>>> e = 1/sin(x)
>>> pprint(e)
  1   
──────
sin(x)
>>> pprint(e.series(x, 0, 4))
           3        
1   x   7⋅x     ⎛ 4⎞
─ + ─ + ──── + O⎝x ⎠
x   6   360

Logical reasoning

Example 1

 
>>> from sympy import *
>>> x = Symbol('x')
>>> y = Symbol('y')
>>> facts = Q.positive(x), Q.positive(y)
>>> with assuming(*facts):
...     print(ask(Q.positive(2 * x + y)))
True

Example 2

 
>>> from sympy import *
>>> x = Symbol('x')
>>> # Assumption about x
>>> fact = [Q.prime(x)]
>>> with assuming(*fact):
...     print(ask(Q.rational(1 / x)))
True
gollark: Fascinating.
gollark: This is why AMD was basically irrelevant for many years until Zen back in 2017 or so.
gollark: Each pair of "cores" shares a bunch of resources, so it isn't really as fast as an actual "core" in other designs, and I think their IPC was quite bad too, so the moderately high clocks didn't do very much except burn power.
gollark: See, while the FX-4100 is allegedly a fairly high-clocked quad-core, this is misleading. AMD's Bulldozer architecture used "clustered multithreading", instead of the "simultaneous multithreading" on modern architectures and also Intel's ones at the time.
gollark: (as this is based on a tower server and not a rack one, you might not even have ridiculously noisy fans in it!)

See also
  • Comparison of computer algebra systems

References
  1. "Releases - sympy/sympy". Retrieved 10 August 2020 – via GitHub.
  2. "SymPy homepage". Retrieved 2014-10-13.
  3. Joyner, David; Čertík, Ondřej; Meurer, Aaron; Granger, Brian E. (2012). "Open source computer algebra systems: SymPy". ACM Communications in Computer Algebra. 45 (3/4): 225–234. doi:10.1145/2110170.2110185.
  4. Meurer, Aaron; Smith, Christopher P.; Paprocki, Mateusz; Čertík, Ondřej; Kirpichev, Sergey B.; Rocklin, Matthew; Kumar, AMiT; Ivanov, Sergiu; Moore, Jason K. (2017-01-02). "SymPy: symbolic computing in Python" (PDF). PeerJ Computer Science. 3: e103. doi:10.7717/peerj-cs.103. ISSN 2376-5992.
  5. https://github.com/sympy/sympy/wiki/SymPy-vs.-Mathematica
  6. "Sympy project statistics on Open HUB". Retrieved 2014-10-13.
  7. Gede, Gilbert; Peterson, Dale L.; Nanjangud, Angadh; Moore, Jason K.; Hubbard, Mont (2013). "Constrained multibody dynamics with Python: From symbolic equation generation to publication". ASME 2013 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference. American Society of Mechanical Engineers: V07BT10A051. doi:10.1115/DETC2013-13470. ISBN 978-0-7918-5597-3.
  8. Rocklin, Matthew; Terrel, Andy (2012). "Symbolic Statistics with SymPy". Computing in Science & Engineering. 14 (3): 88–93. doi:10.1109/MCSE.2012.56.
  9. Asif, Mushtaq; Olaussen, Kåre (2014). "Automatic code generator for higher order integrators". Computer Physics Communications. 185 (5): 1461–1472. arXiv:1310.2111. Bibcode:2014CoPhC.185.1461M. doi:10.1016/j.cpc.2014.01.012.
  10. "Assumptions Module — SymPy 1.4 documentation". docs.sympy.org. Retrieved 2019-07-05.
  11. "Continuum Mechanics — SymPy 1.4 documentation". docs.sympy.org. Retrieved 2019-07-05.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.