Trie

In computer science, a trie, also called digital tree or prefix tree, is a kind of search tree—an ordered tree data structure used to store a dynamic set or associative array where the keys are usually strings. Unlike a binary search tree, no node in the tree stores the key associated with that node; instead, its position in the tree defines the key with which it is associated; i.e., the value of the key is distributed across the structure. All the descendants of a node have a common prefix of the string associated with that node, and the root is associated with the empty string. Keys tend to be associated with leaves, though some inner nodes may correspond to keys of interest. Hence, keys are not necessarily associated with every node. For the space-optimized presentation of prefix tree, see compact prefix tree.

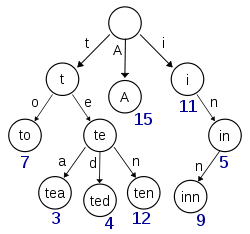
This article is about a tree data structure. For the French commune, see Trie-sur-Baïse.
A trie for keys "A", "to", "tea", "ted", "ten", "i", "in", and "inn". Note that this example does not have all the children alphabetically sorted from left to right as it should be (the root and node 't').

In the example shown, keys are listed in the nodes and values below them. Each complete English word has an arbitrary integer value associated with it. A trie can be seen as a tree-shaped deterministic finite automaton. Each finite language is generated by a trie automaton, and each trie can be compressed into a deterministic acyclic finite state automaton.

Though tries can be keyed by character strings, they need not be. The same algorithms can be adapted to serve similar functions on ordered lists of any construct; e.g., permutations on a list of digits or shapes. In particular, a bitwise trie is keyed on the individual bits making up any fixed-length binary datum, such as an integer or memory address.

History and etymology

Tries were first described by René de la Briandais in 1959.[1][2]:336 The term trie was coined two years later by Edward Fredkin, who pronounces it /ˈtriː/ (as "tree"), after the middle syllable of retrieval.[3][4] However, other authors pronounce it /ˈtraɪ/ (as "try"), in an attempt to distinguish it verbally from "tree".[3][4][5]

Applications

As a replacement for other data structures

As discussed below, a trie has a number of advantages over binary search trees.[6]

A trie can also be used to replace a hash table, over which it has the following advantages:

  • Looking up data in a trie is faster in the worst case, O(m) time (where m is the length of a search string), compared to an imperfect hash table. An imperfect hash table can have key collisions. A key collision is the hash function mapping of different keys to the same position in a hash table. The worst-case lookup speed in an imperfect hash table is O(N) time, but far more typically is O(1), with O(m) time spent evaluating the hash.
  • There are no collisions of different keys in a trie.
  • Buckets in a trie, which are analogous to hash table buckets that store key collisions, are necessary only if a single key is associated with more than one value.
  • There is no need to provide a hash function or to change hash functions as more keys are added to a trie.
  • A trie can provide an alphabetical ordering of the entries by key.

However, a trie also has some drawbacks compared to a hash table:

  • Trie lookup can be slower than hash table lookup, especially if the data is directly accessed on a hard disk drive or some other secondary storage device where the random-access time is high compared to main memory.[7]
  • Some keys, such as floating point numbers, can lead to long chains and prefixes that are not particularly meaningful. Nevertheless, a bitwise trie can handle standard IEEE single and double format floating point numbers.
  • Some tries can require more space than a hash table, as memory may be allocated for each character in the search string, rather than a single chunk of memory for the whole entry, as in most hash tables.

Dictionary representation

A common application of a trie is storing a predictive text or autocomplete dictionary, such as found on a mobile telephone. Such applications take advantage of a trie's ability to quickly search for, insert, and delete entries; however, if storing dictionary words is all that is required (i.e., storage of information auxiliary to each word is not required), a minimal deterministic acyclic finite state automaton (DAFSA) would use less space than a trie. This is because a DAFSA can compress identical branches from the trie which correspond to the same suffixes (or parts) of different words being stored.

Tries are also well suited for implementing approximate matching algorithms,[8] including those used in spell checking and hyphenation[4] software.

Term indexing

A discrimination tree term index stores its information in a trie data structure.[9]

Algorithms

The trie is a tree of nodes which supports Find and Insert operations. Find returns the value for a key string, and Insert inserts a string (the key) and a value into the trie. Both Insert and Find run in O(m) time, where m is the length of the key.

A simple Node class can be used to represent nodes in the trie:

class Node:
   def __init__(self) -> None:
       # Note that using a dictionary for children (as in this implementation)
       # would not by default lexicographically sort the children, which is
       # required by the lexicographic sorting in the Sorting section.
       # For lexicographic sorting, we can instead use an array of Nodes.
       self.children: Dict[str, Node] = {}  # mapping from character to Node
       self.value: Optional[Any] = None

Note that children is a dictionary of characters to a node's children; and it is said that a "terminal" node is one which represents a complete string.
A trie's value can be looked up as follows:

def find(node: Node, key: str) -> Optional[Any]:
    """Find value by key in node."""
    for char in key:
        if char in node.children:
            node = node.children[char]
        else:
            return None
    return node.value

A slight modifications of this routine can be utilized

  • to check if there is any word in the trie that starts with a given prefix (see § Autocomplete), and
  • to return the deepest node corresponding to some prefix of a given string.

Insertion proceeds by walking the trie according to the string to be inserted, then appending new nodes for the suffix of the string that is not contained in the trie:

def insert(node: Node, key: str, value: Any) -> None:
    """Insert key/value pair into node."""
    for char in key:
        if char not in node.children:
            node.children[char] = Node()
        node = node.children[char]
    node.value = value

Deletion of a key can be done lazily (by clearing just the value within the node corresponding to a key), or eagerly by cleaning up any parent nodes that are no longer necessary. Eager deletion is described in the pseudocode here:[10]

def delete(root: Node, key: str) -> bool:
    """
    Eagerly delete the key from the trie rooted at `root`.
    Return whether the trie rooted at `root` is now empty.
    """
    
    def _delete(node: Node, key: str, d: int) -> bool:
        """
        Clear the node corresponding to key[d], and delete the child key[d+1]
        if that subtrie is completely empty, and return whether `node` has been
        cleared.
        """
        if d == len(key):
            node.value = None
        else:
            c = key[d]
            if c in node.children and _delete(node.children[c], key, d+1):
                del node.children[c]
        # Return whether the subtrie rooted at `node` is now completely empty
        return node.value is None and len(node.children) == 0

    return _delete(root, key, 0)

Autocomplete

Tries can be used to return a list of keys with a given prefix. This can also be modified to allow for wildcards in the prefix search.[10]

def keys_with_prefix(root: Node, prefix: str) -> List[str]:
    results: List[str] = []
    x = _get_node(root, prefix)
    _collect(x, list(prefix), results)
    return results

def _collect(x: Optional[Node], prefix: List[str], results: List[str]) -> None:
    """
    Append keys under node `x` matching the given prefix to `results`.
    prefix: list of characters
    """
    if x is None:
        return
    if x.value is not None:
        prefix_str = ''.join(prefix)
        results.append(prefix_str)
    for c in x.children:
        prefix.append(c)
        _collect(x.children[c], prefix, results)
        del prefix[-1]  # delete last character
        
def _get_node(node: Node, key: str) -> Optional[Node]:
    """
    Find node by key. This is the same as the `find` function defined above,
    but returning the found node itself rather than the found node's value.
    """
    for char in key:
        if char in node.children:
            node = node.children[char]
        else:
            return None
    return node

Sorting

Lexicographic sorting of a set of keys can be accomplished by building a trie from them, with the children of each node sorted lexicographically, and traversing it in pre-order, printing only the leaves' values.[11] This algorithm is a form of radix sort.[12]

A trie is the fundamental data structure of Burstsort, which (in 2007) was the fastest known string sorting algorithm due to its efficient cache use.[13] Now there are faster ones.[14]

Full-text search

A special kind of trie, called a suffix tree, can be used to index all suffixes in a text in order to carry out fast full text searches.

Implementation strategies
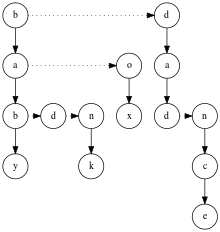
A trie implemented as a left-child right-sibling binary tree: vertical arrows are child pointers, dashed horizontal arrows are next pointers. The set of strings stored in this trie is {baby, bad, bank, box, dad, dance}. The lists are sorted to allow traversal in lexicographic order.

There are several ways to represent tries, corresponding to different trade-offs between memory use and speed of the operations. The basic form is that of a linked set of nodes, where each node contains an array of child pointers, one for each symbol in the alphabet (so for the English alphabet, one would store 26 child pointers and for the alphabet of bytes, 256 pointers). This is simple but wasteful in terms of memory: using the alphabet of bytes (size 256) and four-byte pointers, each node requires a kilobyte of storage, and when there is little overlap in the strings' prefixes, the number of required nodes is roughly the combined length of the stored strings.[2]:341 Put another way, the nodes near the bottom of the tree tend to have few children and there are many of them, so the structure wastes space storing null pointers.[15]

The storage problem can be alleviated by an implementation technique called alphabet reduction, whereby the original strings are reinterpreted as longer strings over a smaller alphabet. E.g., a string of n bytes can alternatively be regarded as a string of 2n four-bit units and stored in a trie with sixteen pointers per node. Lookups need to visit twice as many nodes in the worst case, but the storage requirements go down by a factor of eight.[2]:347–352

An alternative implementation represents a node as a triple (symbol, child, next) and links the children of a node together as a singly linked list: child points to the node's first child, next to the parent node's next child.[15][16] The set of children can also be represented as a binary search tree; one instance of this idea is the ternary search tree developed by Bentley and Sedgewick.[2]:353

Another alternative in order to avoid the use of an array of 256 pointers (ASCII), as suggested before, is to store the alphabet array as a bitmap of 256 bits representing the ASCII alphabet, reducing dramatically the size of the nodes.[17]

Bitwise tries

Bitwise tries are much the same as a normal character-based trie except that individual bits are used to traverse what effectively becomes a form of binary tree. Generally, implementations use a special CPU instruction to very quickly find the first set bit in a fixed length key (e.g., GCC's __builtin_clz() intrinsic). This value is then used to index a 32- or 64-entry table which points to the first item in the bitwise trie with that number of leading zero bits. The search then proceeds by testing each subsequent bit in the key and choosing child[0] or child[1] appropriately until the item is found.

Although this process might sound slow, it is very cache-local and highly parallelizable due to the lack of register dependencies and therefore in fact has excellent performance on modern out-of-order execution CPUs. A red-black tree for example performs much better on paper, but is highly cache-unfriendly and causes multiple pipeline and TLB stalls on modern CPUs which makes that algorithm bound by memory latency rather than CPU speed. In comparison, a bitwise trie rarely accesses memory, and when it does, it does so only to read, thus avoiding SMP cache coherency overhead. Hence, it is increasingly becoming the algorithm of choice for code that performs many rapid insertions and deletions, such as memory allocators (e.g., recent versions of the famous Doug Lea's allocator (dlmalloc) and its descendants). The worst case of steps for lookup is the same as bits used to index bins in the tree.[18]

Alternatively, the term "bitwise trie" can more generally refer to a binary tree structure holding integer values, sorting them by their binary prefix. An example is the x-fast trie.

Compressing tries

Compressing the trie and merging the common branches can sometimes yield large performance gains. This works best under the following conditions:

  • The trie is (mostly) static, so that no key insertions to or deletions are required (e.g., after bulk creation of the trie).
  • Only lookups are needed.
  • The trie nodes are not keyed by node-specific data, or the nodes' data are common.[19]
  • The total set of stored keys is very sparse within their representation space (so compression pays off).

For example, it may be used to represent sparse bitsets; i.e., subsets of a much larger, fixed enumerable set. In such a case, the trie is keyed by the bit element position within the full set. The key is created from the string of bits needed to encode the integral position of each element. Such tries have a very degenerate form with many missing branches. After detecting the repetition of common patterns or filling the unused gaps, the unique leaf nodes (bit strings) can be stored and compressed easily, reducing the overall size of the trie.

Such compression is also used in the implementation of the various fast lookup tables for retrieving Unicode character properties. These could include case-mapping tables (e.g., for the Greek letter pi, from Π to π), or lookup tables normalizing the combination of base and combining characters (like the a-umlaut in German, ä, or the dalet-patah-dagesh-ole in Biblical Hebrew, דַּ֫‎). For such applications, the representation is similar to transforming a very large, unidimensional, sparse table (e.g., Unicode code points) into a multidimensional matrix of their combinations, and then using the coordinates in the hyper-matrix as the string key of an uncompressed trie to represent the resulting character. The compression will then consist of detecting and merging the common columns within the hyper-matrix to compress the last dimension in the key. For example, to avoid storing the full, multibyte Unicode code point of each element forming a matrix column, the groupings of similar code points can be exploited. Each dimension of the hyper-matrix stores the start position of the next dimension, so that only the offset (typically a single byte) need be stored. The resulting vector is itself compressible when it is also sparse, so each dimension (associated to a layer level in the trie) can be compressed separately.

Some implementations do support such data compression within dynamic sparse tries and allow insertions and deletions in compressed tries. However, this usually has a significant cost when compressed segments need to be split or merged. Some tradeoff has to be made between data compression and update speed. A typical strategy is to limit the range of global lookups for comparing the common branches in the sparse trie.

The result of such compression may look similar to trying to transform the trie into a directed acyclic graph (DAG), because the reverse transform from a DAG to a trie is obvious and always possible. However, the shape of the DAG is determined by the form of the key chosen to index the nodes, in turn constraining the compression possible.

Another compression strategy is to "unravel" the data structure into a single byte array.[20] This approach eliminates the need for node pointers, substantially reducing the memory requirements. This in turn permits memory mapping and the use of virtual memory to efficiently load the data from disk.

One more approach is to "pack" the trie.[4] Liang describes a space-efficient implementation of a sparse packed trie applied to automatic hyphenation, in which the descendants of each node may be interleaved in memory.

External memory tries

Several trie variants are suitable for maintaining sets of strings in external memory, including suffix trees. A combination of trie and B-tree, called the B-trie has also been suggested for this task; compared to suffix trees, they are limited in the supported operations but also more compact, while performing update operations faster.[21]

gollark: English is very ambiguous and bad.
gollark: Thus, "random nitpicking".
gollark: Oh, I'm randomly nitpicking.
gollark: It's 70%, and that assumes that the chance of each protest in a location being violent is independent, which is not true.
gollark: I have no idea about *that*, but it's not valid to say "12 protests in your area → guaranteed (i.e. 100% or nearly) chance of one or more being violent".

See also

References
  1. de la Briandais, René (1959). File searching using variable length keys. Proc. Western J. Computer Conf. pp. 295–298. Cited by Brass.
  2. Brass, Peter (2008). Advanced Data Structures. Cambridge University Press.
  3. Black, Paul E. (2009-11-16). "trie". Dictionary of Algorithms and Data Structures. National Institute of Standards and Technology. Archived from the original on 2011-04-29.
  4. Franklin Mark Liang (1983). Word Hy-phen-a-tion By Com-put-er (PDF) (Doctor of Philosophy thesis). Stanford University. Archived (PDF) from the original on 2005-11-11. Retrieved 2010-03-28.
  5. Knuth, Donald (1997). "6.3: Digital Searching". The Art of Computer Programming Volume 3: Sorting and Searching (2nd ed.). Addison-Wesley. p. 492. ISBN 0-201-89685-0.
  6. Bentley, Jon; Sedgewick, Robert (1998-04-01). "Ternary Search Trees". Dr. Dobb's Journal. Dr Dobb's. Archived from the original on 2008-06-23.
  7. Edward Fredkin (1960). "Trie Memory". Communications of the ACM. 3 (9): 490–499. doi:10.1145/367390.367400.
  8. Aho, Alfred V.; Corasick, Margaret J. (Jun 1975). "Efficient String Matching: An Aid to Bibliographic Search" (PDF). Communications of the ACM. 18 (6): 333–340. doi:10.1145/360825.360855.
  9. John W. Wheeler; Guarionex Jordan. "An Empirical Study of Term Indexing in the Darwin Implementation of the Model Evolution Calculus". 2004. p. 5.
  10. Sedgewick, Robert; Wayne, Kevin (June 12, 2020). "Tries". algs4.cs.princeton.edu. Retrieved 2020-08-11.
  11. Kärkkäinen, Juha. "Lecture 2" (PDF). University of Helsinki. The preorder of the nodes in a trie is the same as the lexicographical order of the strings they represent assuming the children of a node are ordered by the edge labels.
  12. Kallis, Rafael (2018). "The Adaptive Radix Tree (Report #14-708-887)" (PDF). University of Zurich: Department of Informatics, Research Publications.
  13. Ranjan Sinha and Justin Zobel and David Ring (Feb 2006). "Cache-Efficient String Sorting Using Copying" (PDF). ACM Journal of Experimental Algorithmics. 11: 1–32. doi:10.1145/1187436.1187439.
  14. J. Kärkkäinen and T. Rantala (2008). "Engineering Radix Sort for Strings". In A. Amir and A. Turpin and A. Moffat (ed.). String Processing and Information Retrieval, Proc. SPIRE. Lecture Notes in Computer Science. 5280. Springer. pp. 3–14. doi:10.1007/978-3-540-89097-3_3.
  15. Allison, Lloyd. "Tries". Retrieved 18 February 2014.
  16. Sahni, Sartaj. "Tries". Data Structures, Algorithms, & Applications in Java. University of Florida. Retrieved 18 February 2014.
  17. Bellekens, Xavier (2014). "A Highly-Efficient Memory-Compression Scheme for GPU-Accelerated Intrusion Detection Systems". Proceedings of the 7th International Conference on Security of Information and Networks - SIN '14. Glasgow, Scotland, UK: ACM. pp. 302:302–302:309. arXiv:1704.02272. doi:10.1145/2659651.2659723. ISBN 978-1-4503-3033-6.
  18. Lee, Doug. "A Memory Allocator". Retrieved 1 December 2019. HTTP for Source Code. Binary Trie is described in Version 2.8.6, Section "Overlaid data structures", Structure "malloc_tree_chunk".
  19. Jan Daciuk; Stoyan Mihov; Bruce W. Watson; Richard E. Watson (2000). "Incremental Construction of Minimal Acyclic Finite-State Automata". Computational Linguistics. Association for Computational Linguistics. 26: 3–16. arXiv:cs/0007009. doi:10.1162/089120100561601. Archived from the original on 2011-09-30. Retrieved 2009-05-28. This paper presents a method for direct building of minimal acyclic finite states automaton which recognizes a given finite list of words in lexicographical order. Our approach is to construct a minimal automaton in a single phase by adding new strings one by one and minimizing the resulting automaton on-the-fly Alt URL
  20. Ulrich Germann; Eric Joanis; Samuel Larkin (2009). "Tightly packed tries: how to fit large models into memory, and make them load fast, too" (PDF). ACL Workshops: Proceedings of the Workshop on Software Engineering, Testing, and Quality Assurance for Natural Language Processing. Association for Computational Linguistics. pp. 31–39. We present Tightly Packed Tries (TPTs), a compact implementation of read-only, compressed trie structures with fast on-demand paging and short load times. We demonstrate the benefits of TPTs for storing n-gram back-off language models and phrase tables for statistical machine translation. Encoded as TPTs, these databases require less space than flat text file representations of the same data compressed with the gzip utility. At the same time, they can be mapped into memory quickly and be searched directly in time linear in the length of the key, without the need to decompress the entire file. The overhead for local decompression during search is marginal.
  21. Askitis, Nikolas; Zobel, Justin (2008). "B-tries for Disk-based String Management" (PDF). VLDB Journal: 1–26. ISSN 1066-8888.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.