2–3 tree

In computer science, a 2–3 tree is a tree data structure, where every node with children (internal node) has either two children (2-node) and one data element or three children (3-nodes) and two data elements. A B-tree of order 3 is a 2-3 tree.[1] Nodes on the outside of the tree (leaf nodes) have no children and one or two data elements.[2][3] 2−3 trees were invented by John Hopcroft in 1970.[4]

2-3 tree
Typetree
Invented1970
Invented byJohn Hopcroft
Time complexity in big O notation
Algorithm Average Worst case
Space O(n) O(n)
Search O(log n) O(log n)
Insert O(log n) O(log n)
Delete O(log n) O(log n)

2–3 trees are required to be balanced, meaning that each leaf is at the same level. It follows that each right, center, and left subtree of a node contains the same or close to the same amount of data.

Definitions

We say that an internal node is a 2-node if it has one data element and two children.

We say that an internal node is a 3-node if it has two data elements and three children.

A 4-node, with three data elements, may be temporarily created during manipulation of the tree but is never persistently stored in the tree.

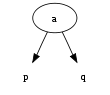  • 2 node
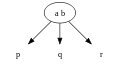  • 3 node

We say that T is a 2–3 tree if and only if one of the following statements hold:[5]

  • T is empty. In other words, T does not have any nodes.
  • T is a 2-node with data element a. If T has left child p and right child q, then
    • p and q are non-empty 2–3 trees of the same height;
    • a is greater than each element in p; and
    • a is less than or equal to each data element in q.
  • T is a 3-node with data elements a and b, where a < b. If T has left child p, middle child q, and right child r, then
    • p, q, and r are non-empty 2–3 trees of equal height;
    • a is greater than each data element in p and less than or equal to each data element in q; and
    • b is greater than each data element in q and less than or equal to each data element in r.

Properties
  • Every internal node is a 2-node or a 3-node.
  • All leaves are at the same level.
  • All data is kept in sorted order.

Operations

Searching

Searching for an item in a 2–3 tree is similar to searching for an item in a binary search tree. Since the data elements in each node are ordered, a search function will be directed to the correct subtree and eventually to the correct node which contains the item.

  1. Let T be a 2–3 tree and d be the data element we want to find. If T is empty, then d is not in T and we're done.
  2. Let t be the root of T.
  3. Suppose t is a leaf.
    • If d is not in t, then d is not in T. Otherwise, d is in T. We need no further steps and we're done.
  4. Suppose t is a 2-node with left child p and right child q. Let a be the data element in t. There are three cases:
    • If d is equal to a, then we've found d in T and we're done.
    • If , then set T to p, which by definition is a 2–3 tree, and go back to step 2.
    • If , then set T to q and go back to step 2.
  5. Suppose t is a 3-node with left child p, middle child q, and right child r. Let a and b be the two data elements of t, where . There are four cases:
    • If d is equal to a or b, then d is in T and we're done.
    • If , then set T to p and go back to step 2.
    • If , then set T to q and go back to step 2.
    • If , then set T to r and go back to step 2.

Insertion

Insertion maintains the balanced property of the tree.[5]

To insert into a 2-node, the new key is added to the 2-node in the appropriate order.

To insert into a 3-node, more work may be require depending on the location of the 3-node. If the tree consists only of a 3-node, the node is split into three 2-nodes with the appropriate keys and children.

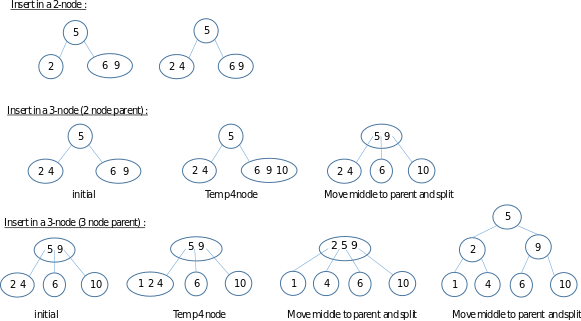
Insertion of a number in a 2-3 tree for 3 possible cases.

If the target node is a 3-node whose parent is a 2-node, the key is inserted into the 3-node to create a temporary 4-node. In the illustration, the key 10 is inserted into the 2-node with 6 and 9. The middle key is 9, and is promoted to the parent 2-node. This leaves a 3-node of 6 and 10, which is split to be two 2-nodes held as children of the parent 3-node.

If the target node is a 3-node and the parent is a 3-node, a temporary 4-node is created then split as above. This process continues up the tree to the root. If the root must be split, then the process of a single 3-node is followed: a temporary 4-node root is split into three 2-nodes, one of which is considered to be the root. This operation grows the height of the tree by one.

Parallel operations

Since 2-3 trees are similar in structure to red-black trees, parallel algorithms for red-black trees can be applied to 2-3 trees as well.

gollark: Lots of them are my random/old CC projects.
gollark: ++about
gollark: discord.py, currently.
gollark: Nope.
gollark: That's weird, the regex is acting strangely.

See also

References
  1. Knuth, Donald M (1998). "6.2.4". The Art of Computer Programming. 3 (2 ed.). Addison Wesley. ISBN 9780201896855. The 2-3 trees defined at the close of Section 6.2.3 are equivalent to B-Trees of order 3.
  2. Gross, R. Hernández, J. C. Lázaro, R. Dormido, S. Ros (2001). Estructura de Datos y Algoritmos. Prentice Hall. ISBN 84-205-2980-X.
  3. Aho, Alfred V.; Hopcroft, John E.; Ullman, Jeffrey D. (1974). The Design and Analysis of Computer Algorithms. Addison-Wesley., p.145-147
  4. Cormen, Thomas (2009). Introduction to Algorithms. London: The MIT Press. pp. 504. ISBN 978-0262033848.
  5. Sedgewick, Robert; Wayne, Kevin. "3.3". Algorithms (4 ed.). Addison Wesley. ISBN 9780321573513.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.