Tideman alternative method

Tideman's Alternative Methods, including Alternative Smith and Alternative Schwartz, are two electoral systems developed by Nicolaus Tideman which select a single winner using votes that express preferences. These methods can also create a sorted list of winners.

These methods are Smith- and Schwartz-efficient, respectively, and thus are Condorcet methods.

Procedure

Tideman's Alternative Smith with three in the Smith set

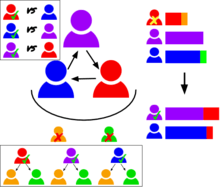
Tideman's Alternative procedure is as follows:

1. Identify the Smith or Schwartz set.
2. If the set consists of one candidate, elect that candidate.
3. Eliminate all candidates outside the set and redistribute ballots.
4. eliminate the plurality loser.
5. Repeat the procedure.

To create a sorted list of preferred candidates, select a winner, remove that winner from the list of candidates, and repeat.

Features

Tideman's Alternative Methods are easier to understand than other methods, such as Ranked Pairs and Schulze, owing to the simplicity of explaining both the Smith set (the smallest set of all candidates who each defeat every non-Smith candidate) and Instant run-off voting (eliminating the candidate with the fewest votes). This increases the likelihood of voter acceptance.

This method strongly resists both tactical voting and tactical nomination, reducing the amount of political manipulation possible or favorable in large elections. They inherit this resistance from instant run-off voting, as both methods resolve a Condorcet winner from the Smith set by eliminating non-Smith (or non-Schwartz) candidates and performing instant run-off voting on the result.

Although IRV itself faces criticism for theoretical and historical failures, all Smith- and Schwartz-efficient voting methods attempt to resolve a candidate from these respective sets. Unlike IRV, these methods invariably elect a Condorcet winner; when there is none, they elect different winners based on arbitrary criteria. Ranked Pairs elects the winner with the strongest overall ranking, while the Schulze method attempts to elect a winner without the worst pairwise loss. Tideman's Alternative Method elects a candidate in a manner strongly resisting tactical nomination and voting.

Tideman's Alternative Methods fail independence of irrelevant alternatives. However, the methods adhere to a less strict property, sometimes called independence of Smith-dominated alternatives (ISDA). It says that if one candidate (X) wins an election, and a new alternative (Y) is added, X will win the election if Y is not in the Smith set. ISDA implies the Smith criterion and Condorcet criterion.

Note that the Condorcet winner can be used as the "set" (if there is a Condorcet winner, they are the only member of the set. Otherwise, all candidates are in the set). This variation is known as Benham's method.

Comparison table

The following table compares Tideman's Alternative Methods with other preferential single-winner election methods:

Comparison of Preferential Electoral Systems

	Monotonic	Condorcet	Majority	Condorcet loser	Majority loser	Mutual majority	Smith	ISDA	LIIA	Clone independence	Reversal symmetry	Participation, Consistency	Later-no‑harm	Later-no‑help	Polynomial time	Resolvability
Schulze	Yes	Yes	Yes	Yes	Yes	Yes	Yes	Yes	No	Yes	Yes	No	No	No	Yes	Yes
Ranked pairs	Yes	Yes	Yes	Yes	Yes	Yes	Yes	Yes	Yes	Yes	Yes	No	No	No	Yes	Yes
Tideman's Alternative	No	Yes	Yes	Yes	Yes	Yes	Yes	Yes	No	Yes	No	No	No	No	Yes	Yes
Kemeny–Young	Yes	Yes	Yes	Yes	Yes	Yes	Yes	Yes	Yes	No	Yes	No	No	No	No	Yes
Copeland	Yes	Yes	Yes	Yes	Yes	Yes	Yes	Yes	No	No	Yes	No	No	No	Yes	No
Nanson	No	Yes	Yes	Yes	Yes	Yes	Yes	No	No	No	Yes	No	No	No	Yes	Yes
Instant-runoff voting	No	No	Yes	Yes	Yes	Yes	No	No	No	Yes	No	No	Yes	Yes	Yes	Yes
Borda	Yes	No	No	Yes	Yes	No	No	No	No	No	Yes	Yes	No	Yes	Yes	Yes
Baldwin	No	Yes	Yes	Yes	Yes	Yes	Yes	No	No	No	No	No	No	No	Yes	Yes
Bucklin	Yes	No	Yes	No	Yes	Yes	No	No	No	No	No	No	No	Yes	Yes	Yes
Plurality	Yes	No	Yes	No	No	No	No	No	No	No	No	Yes	Yes	Yes	Yes	Yes
Contingent voting	No	No	Yes	Yes	Yes	No	No	No	No	No	No	No	Yes	Yes	Yes	Yes
Coombs[1]	No	No	Yes	Yes	Yes	Yes	No	No	No	No	No	No	No	No	Yes	Yes
MiniMax	Yes	Yes	Yes	No	No	No	No	No	No	No	No	No	No	No	Yes	Yes
Anti-plurality[1]	Yes	No	No	No	Yes	No	No	No	No	No	No	Yes	No	No	Yes	Yes
Sri Lankan contingent voting	No	No	Yes	No	No	No	No	No	No	No	No	No	Yes	Yes	Yes	Yes
Supplementary voting	No	No	Yes	No	No	No	No	No	No	No	No	No	Yes	Yes	Yes	Yes
Dodgson[1]	No	Yes	Yes	No	No	No	No	No	No	No	No	No	No	No	No	Yes

References

• Green-Armytage, James. Four Condorcet-Hare Hybrid Methods for Single-Winner Elections.

1. Anti-plurality, Coombs and Dodgson are assumed to receive truncated preferences by apportioning possible rankings of unlisted alternatives equally; for example, ballot A > B = C is counted as ${\displaystyle {\tfrac {1}{2}}}$ A > B > C and ${\displaystyle {\tfrac {1}{2}}}$ A > C > B. If these methods are assumed not to receive truncated preferences, then Later-no-harm and Later-no-help are not applicable.