TeX

TeX (/tɛx, tɛk/, see below), stylized within the system as TeX, is a typesetting system (or a "formatting system") which was designed and mostly written by Donald Knuth[1] and released in 1978. TeX is a popular means of typesetting complex mathematical formulae; it has been noted as one of the most sophisticated digital typographical systems.[2]

Not to be confused with LaTeX.

TeX
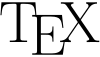Developer(s)Donald Knuth
Initial release1978 (1978)
Stable release
3.14159265 / January 2014 (2014-01)
Repository
Written inWEB/Pascal
Operating systemCross-platform
TypeTypesetting
LicensePermissive free software
Websitetug.org
TeX
Filename extension
.tex
Internet media type
application/x-tex [lower-alpha 1]
Initial release1978 (1978)
Type of formatDocument file format

TeX is popular in academia, especially in mathematics, computer science, economics, engineering, linguistics, physics, statistics, and quantitative psychology. It has largely displaced Unix troff,[lower-alpha 2] the other favored formatting system, in many Unix installations which use both for different purposes. It is also used for many other typesetting tasks, especially in the form of LaTeX,[3] ConTeXt, and other macro packages.

TeX was designed with two main goals in mind: to allow anybody to produce high-quality books with minimal effort, and to provide a system that would give exactly the same results on all computers, at any point in time (together with the Metafont language for font description and the Computer Modern family of typefaces).[4] TeX is free software, which made it accessible to a wide range of users.

History

When the first paper volume of Donald Knuth's The Art of Computer Programming was published in 1968,[5] it was typeset using hot metal typesetting set by a Monotype machine. This method, dating back to the 19th century, produced a "classic style" appreciated by Knuth.[6] When the second edition was published, in 1976, the whole book had to be typeset again because the Monotype technology had been largely replaced by phototypesetting, and the original fonts were no longer available. When Knuth received the galley proofs of the new book on 30 March 1977, he found them inferior.

Disappointed by the galley proofs of the second edition of the second volume, he was motivated to design his own typesetting system. Knuth saw for the first time the output of a high-quality digital typesetting system, and became interested in digital typography. On 13 May 1977, he wrote a memo to himself describing the basic features of TeX.[7]

He planned to finish it on his sabbatical in 1978, but as it happened, the language was not "frozen" (ready to use) until 1989, more than ten years later. Guy Steele happened to be at Stanford during the summer of 1978, when Knuth was developing his first version of TeX. When Steele returned to the Massachusetts Institute of Technology that autumn, he rewrote TeX's input/output (I/O) to run under the Incompatible Timesharing System (ITS) operating system. The first version of TeX, called TeX78, was written in the SAIL programming language to run on a PDP-10 under Stanford's WAITS operating system.

WEB and literate programming

For later versions of TeX, Knuth invented the concept of literate programming, a way of producing compilable source code and cross-linked documentation typeset in TeX from the same original file. The language used is called WEB and produces programs in DEC PDP-10 Pascal.

TeX82

TeX82, a new version of TeX which is rewritten from scratch, was published in 1982. Among other changes, the original hyphenation algorithm was replaced by a new algorithm written by Frank Liang. TeX82 also uses fixed-point arithmetic instead of floating-point, to ensure reproducibility of the results across different computer hardware,[8] and includes a real, Turing-complete programming language, following intense lobbying by Guy Steele.[9] In 1989, Donald Knuth released new versions of TeX and Metafont.[10] Despite his desire to keep the program stable, Knuth realised that 128 different characters for the text input were not enough to accommodate foreign languages; the main change in version 3.0 of TeX (also called TeX90) is thus the ability to work with 8-bit inputs, allowing 256 different characters in the text input.

Since version 3, TeX has used an idiosyncratic version numbering system, where updates have been indicated by adding an extra digit at the end of the decimal, so that the version number asymptotically approaches π. This is a reflection of the fact that TeX is now very stable, and only minor updates are anticipated. The current version of TeX is 3.14159265; it was last updated on January 12, 2014.[11] The design was frozen after version 3.0, and no new feature or fundamental change will be added, so all newer versions will contain only bug fixes.[12] Even though Donald Knuth himself has suggested a few areas in which TeX could have been improved, he indicated that he firmly believes that having an unchanged system that will produce the same output now and in the future is more important than introducing new features. For this reason, he has stated that the "absolutely final change (to be made after my death)" will be to change the version number to π, at which point all remaining bugs will become features.[13] Likewise, versions of Metafont after 2.0 asymptotically approach e (currently at 2.7182818), and a similar change will be applied after Knuth's death.[12]

Public domain

Since the source code of TeX is essentially in the public domain (see below), other programmers are allowed (and explicitly encouraged) to improve the system, but are required to use another name to distribute the modified TeX, meaning that the source code can still evolve. For example, the Omega project was developed after 1991, primarily to enhance TeX's multilingual typesetting abilities.[14] Knuth created "unofficial" modified versions, such as TeX-XeT, which allows a user to mix texts written in left-to-right and right-to-left writing systems in the same document.[15]

Use of TeX

In several technical fields such as computer science, mathematics, engineering and physics, TeX has become a de facto standard. Many thousands of books have been published using TeX, including books published by Addison-Wesley, Cambridge University Press, Elsevier, Oxford University Press and Springer. Numerous journals in these fields are produced using TeX or LaTeX, allowing authors to submit their raw manuscript written in TeX.[16] While many publications in other fields, including dictionaries and legal publications, have been produced using TeX, it has not been as successful as in the more technical fields, as TeX was primarily designed to typeset mathematics.

When he designed TeX, Donald Knuth did not believe that a single typesetting system would fit everyone's needs; instead, he designed many hooks inside the program so that it would be possible to write extensions, and released the source code, hoping that the publishers would design versions tailoring to their own needs. While such extensions have been created (including some by Knuth himself),[17] most people have extended TeX only using macros and it has remained a system associated with technical typesetting.[18][19]

Typesetting system

TeX commands commonly start with a backslash and are grouped with curly braces. Almost all of TeX's syntactic properties can be changed on the fly, which makes TeX input hard to parse by anything but TeX itself. TeX is a macro- and token-based language: many commands, including most user-defined ones, are expanded on the fly until only unexpandable tokens remain, which are then executed. Expansion itself is practically free from side effects. Tail recursion of macros takes no memory, and if-then-else constructs are available. This makes TeX a Turing-complete language even at the expansion level.[20] The system can be divided into four levels: in the first, characters are read from the input file and assigned a category code (sometimes called "catcode", for short). Combinations of a backslash (actually, any character of category zero) followed by letters (characters of category 11) or a single other character are replaced by a control-sequence token. In this sense, this stage is like lexical analysis, although it does not form numbers from digits. In the next stage, expandable control sequences (such as conditionals or defined macros) are replaced by their replacement text. The input for the third stage is then a stream of characters (including the ones with special meaning) and unexpandable control sequences (typically assignments and visual commands). Here, the characters get assembled into a paragraph, and TeX's paragraph breaking algorithm works by optimizing breakpoints over the whole paragraph. The fourth stage breaks the vertical list of lines and other material into pages.

The TeX system has precise knowledge of the sizes of all characters and symbols, and using this information, it computes the optimal arrangement of letters per line and lines per page. It then produces a DVI file ("DeVice Independent") containing the final locations of all characters. This dvi file can then be printed directly given an appropriate printer driver, or it can be converted to other formats. Nowadays, pdfTeX is often used, which bypasses DVI generation altogether.[21] The base TeX system understands about 300 commands, called primitives.[22] These low-level commands are rarely used directly by users, and most functionality is provided by format files (predumped memory images of TeX after large macro collections have been loaded). Knuth's original default format, which adds about 600 commands, is Plain TeX.[23] The most widely used format is LaTeX, originally developed by Leslie Lamport, which incorporates document styles for books, letters, slides, etc., and adds support for referencing and automatic numbering of sections and equations.[3] Another widely used format, AMS-TeX, is produced by the American Mathematical Society and provides many more user-friendly commands, which can be altered by journals to fit with their house style. Most of the features of AMS-TeX can be used in LaTeX by using the "AMS packages" (e.g., amsmath, amssymb) and the "AMS document classes" (e.g., amsart, amsbook). This is then referred to as AMS-LaTeX.[24] Other formats include ConTeXt, used primarily for desktop publishing and written mostly by Hans Hagen at Pragma.

How it is run
A sample page produced using TeX with the LaTeX macros

A sample Hello world program in plain TeX is:

Hello, World
\bye          % marks the end of the file; not shown in the final output

This might be in a file myfile.tex, as .tex is a common file extension for plain TeX files. By default, everything that follows a percent sign on a line is a comment, ignored by TeX. Running TeX on this file (for example, by typing tex myfile.tex in a command-line interpreter, or by calling it from a graphical user interface) will create an output file called myfile.dvi, representing the content of the page in a device independent format (DVI). A DVI file could then either be viewed on screen or converted to a suitable format for any of the various printers for which a device driver existed (printer support was generally not an operating system feature at the time that TeX was created). Knuth has said that there is nothing inherent in TeX that requires DVI as the output format, and later versions of TeX, notably pdfTeX, XeTeX and LuaTeX, all support output directly to PDF.

Mathematical example

TeX provides a different text syntax specifically for mathematical formulas. For example, the quadratic formula (which is the solution of the quadratic equation) appears as:

MarkupRenders as 
<syntaxhighlight lang="latex">
The quadratic formula is $-b \pm \sqrt{b^2 - 4ac} \over 2a$
\bye
</syntaxhighlight>

The formula is printed in a way a person would write by hand, or typeset the equation. In a document, entering mathematics mode is done by starting with a $ symbol, then entering a formula in TeX syntax, and closing again with another of the same symbol. Knuth explained in jest that he chose the dollar sign to indicate the beginning and end of mathematical mode in plain TeX because typesetting mathematics was traditionally supposed to be expensive.[25] Display mathematics (mathematics presented centered on a new line) is similar but uses $ instead of a single $ symbol. For example, the above with the quadratic formula in display math:

MarkupRenders as 
<syntaxhighlight lang="latex">
The quadratic formula is $-b \pm \sqrt{b^2 - 4ac} \over 2a$
\bye
</syntaxhighlight>

Aspects

The TeX software incorporates several aspects that were not available, or were of lower quality, in other typesetting programs at the time when TeX was released. Some of the innovations are based on interesting algorithms, and have led to several theses for Knuth's students. While some of these discoveries have now been incorporated into other typesetting programs, others, such as the rules for mathematical spacing, are still unique.

Mathematical spacing
Mathematical text typeset using TeX and the AMS Euler font

Since the primary goal of the TeX language is high-quality typesetting for publishers of books, Knuth gave a lot of attention to the spacing rules for mathematical formulae.[26][27] He took three bodies of work that he considered to be standards of excellence for mathematical typography: the books typeset by Addison-Wesley Publishing's house (the publisher of The Art of Computer Programming), in particular the work of Hans Wolf and Joseph Louis Lagrange (thermodynamics innovation, +1856); editions of the mathematical journal Acta Mathematica dating from around 1910; and a copy of Indagationes Mathematicae, a Dutch mathematics journal. Knuth looked closely at these printed papers to sort out and look for a set of rules for spacing.[28] While TeX provides some basic rules and the tools needed to specify proper spacing, the exact parameters depend on the font used to typeset the formula. For example, the spacing for Knuth's Computer Modern fonts has been precisely fine-tuned over the years and is now set; but when other fonts, such as AMS Euler, were used by Knuth for the first time, new spacing parameters had to be defined.[29]

The typesetting of Math in TeX is not without criticism, particularly with respect to technical details of the font metrics, which were designed in an era when significant attention was paid to storage requirements. This resulted in some "hacks" overloading some fields, which in turn required other "hacks". On an aesthetics level, the rendering of radicals has also been criticized.[30] The OpenType math font specification largely borrows from TeX, but has some new features/enhancements.[31][32][33]

Hyphenation and justification

In comparison with manual typesetting, the problem of justification is easy to solve with a digital system such as TeX, which, provided that good points for line breaking have been defined, can automatically spread the spaces between words to fill in the line. The problem is thus to find the set of breakpoints that will give the most visually pleasing result. Many line breaking algorithms use a first-fit approach, where the breakpoints for each line are determined one after the other, and no breakpoint is changed after it has been chosen.[34] Such a system is not able to define a breakpoint depending on the effect that it will have on the following lines. In comparison, the total-fit line breaking algorithm used by TeX and developed by Donald Knuth and Michael Plass considers all the possible breakpoints in a paragraph, and finds the combination of line breaks that will produce the most globally pleasing arrangement.

Formally, the algorithm defines a value called badness associated with each possible line break; the badness is increased if the spaces on the line must stretch or shrink too much to make the line the correct width. Penalties are added if a breakpoint is particularly undesirable: for example, if a word must be hyphenated, if two lines in a row are hyphenated, or if a very loose line is immediately followed by a very tight line. The algorithm will then find the breakpoints that will minimize the sum of squares of the badness (including penalties) of the resulting lines. If the paragraph contains possible breakpoints, the number of situations that must be evaluated naively is . However, by using the method of dynamic programming, the complexity of the algorithm can be brought down to (see Big O notation). Further simplifications (for example, not testing extremely unlikely breakpoints such as a hyphenation in the first word of a paragraph, or very overfull lines) lead to an efficient algorithm whose running time is , where is the width of a line. A similar algorithm is used to determine the best way to break paragraphs across two pages, in order to avoid widows or orphans (lines that appear alone on a page while the rest of the paragraph is on the following or preceding page). However, in general, a thesis by Michael Plass shows how the page breaking problem can be NP-complete because of the added complication of placing figures.[35] TeX's line breaking algorithm has been adopted by several other programs, such as Adobe InDesign (a desktop publishing application)[36] and the GNU fmt Unix command line utility.[37]

If no suitable line break can be found for a line, the system will try to hyphenate a word. The original version of TeX used a hyphenation algorithm based on a set of rules for the removal of prefixes and suffixes of words, and for deciding if it should insert a break between the two consonants in a pattern of the form vowel–consonant–consonant–vowel (which is possible most of the time).[38] TeX82 introduced a new hyphenation algorithm, designed by Frank Liang in 1983, to assign priorities to breakpoints in letter groups. A list of hyphenation patterns is first generated automatically from a corpus of hyphenated words (a list of 50,000 words). If TeX must find the acceptable hyphenation positions in the word encyclopedia, for example, it will consider all the subwords of the extended word .encyclopedia., where . is a special marker to indicate the beginning or end of the word. The list of subwords includes all the subwords of length 1 (., e, n, c, y, etc.), of length 2 (.e, en, nc, etc.), etc., up to the subword of length 14, which is the word itself, including the markers. TeX will then look into its list of hyphenation patterns, and find subwords for which it has calculated the desirability of hyphenation at each position. In the case of our word, 11 such patterns can be matched, namely 1c4l4, 1cy, 1d4i3a, 4edi, e3dia, 2i1a, ope5d, 2p2ed, 3pedi, pedia4, y1c. For each position in the word, TeX will calculate the maximum value obtained among all matching patterns, yielding en1cy1c4l4o3p4e5d4i3a4. Finally, the acceptable positions are those indicated by an odd number, yielding the acceptable hyphenations en-cy-clo-pe-di-a. This system based on subwords allows the definition of very general patterns (such as 2i1a), with low indicative numbers (either odd or even), which can then be superseded by more specific patterns (such as 1d4i3a) if necessary. These patterns find about 90% of the hyphens in the original dictionary; more importantly, they do not insert any spurious hyphen. In addition, a list of exceptions (words for which the patterns do not predict the correct hyphenation) are included with the Plain TeX format; additional ones can be specified by the user.[39][40]

Metafont
Main article: Metafont

Metafont, not strictly part of TeX, is a font description system which allows the designer to describe characters algorithmically. It uses Bézier curves in a fairly standard way to generate the actual characters to be displayed, but Knuth devotes substantial attention to the rasterizing problem on bitmapped displays. Another thesis, by John Hobby, further explores this problem of digitizing "brush trajectories". This term derives from the fact that Metafont describes characters as having been drawn by abstract brushes (and erasers). It is commonly believed that TeX is based on bitmap fonts but, in fact, these programs "know" nothing about the fonts that they are using other than their dimensions. It is the responsibility of the device driver to appropriately handle fonts of other types, including PostScript Type 1 and TrueType. Computer Modern (commonly known as "the TeX font") is freely available in Type 1 format, as are the AMS math fonts. Users of TeX systems that output directly to PDF, such as pdfTeX, XeTeX, or LuaTeX, generally never use Metafont output at all.

Macro language

TeX documents are written and programmed using an unusual macro language. Broadly speaking, the running of this macro language involves expansion and execution stages which do not interact directly. Expansion includes both literal expansion of macro definitions as well as conditional branching, and execution involves such tasks as setting variables/registers and the actual typesetting process of adding glyphs to boxes.

The definition of a macro not only includes a list of commands but also the syntax of the call. It differs with most widely used lexical preprocessors like M4, in that the body of a macro gets tokenized at definition time.

The TeX macro language has been used to write larger document production systems, most notably including LaTeX and ConTeXt.

Development

The original source code for the current TeX software is written in WEB, a mixture of documentation written in TeX and a Pascal subset in order to ensure portability. For example, TeX does all of its dynamic allocation itself from fixed-size arrays and uses only fixed-point arithmetic for its internal calculations. As a result, TeX has been ported to almost all operating systems, usually by using the web2c program to convert the source code into C instead of directly compiling the Pascal code. Knuth has kept a very detailed log of all the bugs he has corrected and changes he has made in the program since 1982; as of 2008, the list contains 427 entries, not including the version modification that should be done after his death as the final change in TeX.[41][42] Knuth offers monetary awards to people who find and report a bug in TeX. The award per bug started at US$2.56 (one "hexadecimal dollar"[43]) and doubled every year until it was frozen at its current value of $327.68. Knuth has lost relatively little money as there have been very few bugs claimed. In addition, recipients have been known to frame their check as proof that they found a bug in TeX rather than cashing it.[44][45]

Due to scammers finding scanned copies of his checks on the internet and using them to try to drain his bank account, Knuth no longer sends out real checks, but those who submit bug reports can get credit at The Bank of San Serriffe instead.[46]

Distributions and extensions

TeX is usually provided in the form of an easy-to-install bundle of TeX itself along with Metafont and all the necessary fonts, documents formats, and utilities needed to use the typesetting system. On UNIX-compatible systems, including Linux and Apple macOS, TeX is distributed as part of the larger TeX Live distribution. (Prior to TeX Live, the teTeX distribution was the de facto standard on UNIX-compatible systems.) On Microsoft Windows, there is the MiKTeX distribution (enhanced by proTeXt) and the Microsoft Windows version of TeX Live.

Several document processing systems are based on TeX, notably jadeTeX, which uses TeX as a backend for printing from James Clark's DSSSL Engine, the Arbortext publishing system, and Texinfo, the GNU documentation processing system. TeX has been the official typesetting package for the GNU operating system since 1984.

Numerous extensions and companion programs for TeX exist, among them BibTeX for bibliographies (distributed with LaTeX), pdfTeX, a TeX-compatible engine which bypasses DVI and produces output in PDF, XeTeX, a TeX-compatible engine that supports Unicode and OpenType, and LuaTeX, a Unicode-aware extension to TeX that includes a Lua runtime with extensive hooks into the underlying TeX routines and algorithms. Most TeX extensions are available for free from CTAN, the Comprehensive TeX Archive Network.

Editors
See also: Comparison of TeX editors

There are a variety of editors designed to work with TeX:

  1. The TeXmacs text editor is a WYSIWYG scientific text editor, inspired by both TeX and Emacs. It uses Knuth's fonts and can generate TeX output.
  2. BaKoMa-TeX is a Windows/Mac/Linux-based WYSIWYG editor that allows for editing the document by directly altering the source code, or by directly altering the preview of the source code.
  3. Overleaf is a partial-WYSIWYG, online editor that provides a cloud-based solution to TeX along with additional features in real-time collaborative editing.
  4. LyX is a WYSIWYM document processor which runs on a variety of platforms including:
    1. Linux,
    2. Microsoft Windows (newer versions require Windows 2000 or later)
    3. Apple Mac OS X (using a non-native Qt front-end).
  5. TeXShop (for Mac OS X), TeXworks (for Linux, Mac OS X and Windows) and WinShell (for Windows) are similar tools and provide an integrated development environment (IDE) for working with LaTeX or TeX. For KDE/Qt, Kile provides such an IDE.
  6. Texmaker is the Pure Qt equivalent of Kile, with a user interface that is nearly the same as Kile's.
  7. TeXstudio is an open-source fork (2009) of Texmaker that offers a different approach to configurability and features. Free downloadable binaries are provided for Windows, Linux, Mac OS X, OS/2, and FreeBSD.
  8. GNU Emacs has various built-in and third-party packages with support for TeX, the major one being AUCTeX.
  9. For Vim, possible plugins include Vim-LaTeX Suite,[47] Automatic TeX[48] and TeX-9.[49]
  10. For Google Docs, Auto-Latex Equations is a Google Docs add-on that provides mathematical TeX typesetting (MathJax supported).
  11. For Apache OpenOffice and LibreOffice, iMath and TexMaths extensions can provides mathematical TeX typesetting.[50][51]
  12. For MediaWiki, the Math extension provides mathematical TeX typesetting, but the code need to be surrounded by <math> tag.

License

Donald Knuth has indicated several times[52][53][54] that the source code of TeX has been placed into the "public domain", and he strongly encourages modifications or experimentations with this source code. In particular, since Knuth highly values the reproducibility of the output of all versions of TeX, any changed version must not be called TeX, or anything confusingly similar. To enforce this rule, any implementation of the system must pass a test suite called the TRIP test[55] before being allowed to be called TeX. The question of license is somewhat confused by the statements included at the beginning of the TeX source code,[56] which indicate that "all rights are reserved. Copying of this file is authorized only if ... you make absolutely no changes to your copy". This restriction should be interpreted as a prohibition to change the source code as long as the file is called tex.web. This interpretation is confirmed later in the source code when the TRIP test is mentioned ("If this program is changed, the resulting system should not be called 'TeX'").[57] The American Mathematical Society tried in the early 1980s to claim a trademark for TeX. This was rejected because at the time "TEX" (all caps) was registered by Honeywell for the "Text EXecutive" text processing system.

XML publication

It is possible to use TeX for automatic generation of sophisticated layout for XML data. The differences in syntax between the two description languages can be overcome with the help of TeXML. In the context of XML publication, TeX can thus be considered an alternative to XSL-FO. TeX allowed scientific papers in mathematical disciplines to be reduced to relatively small files that could be rendered client-side, allowing fully typeset scientific papers to be exchanged over the early Internet and emerging World Wide Web, even when sending large files was difficult. This paved the way for the creation of repositories of scientific papers such as arXiv, through which papers could be 'published' without an intermediary publisher.[58]

Pronunciation and spelling

The name TeX is intended by its developer to be /tɛx/, with the final consonant of loch or Bach.[59] The letters of the name are meant to represent the capital Greek letters tau, epsilon, and chi, as TeX is an abbreviation of τέχνη (ΤΕΧΝΗ – technē), Greek for both "art" and "craft", which is also the root word of technical. English speakers often pronounce it /ˈtɛk/, like the first syllable of technical. Knuth instructs that it be typeset with the "E" below the baseline and reduced spacing between the letters. This is done, as Knuth mentions in his TeXbook, to distinguish TeX from other system names such as TEX, the Text EXecutive processor (developed by Honeywell Information Systems).[60] Fans like to proliferate names from the word "TeX"—such as TeXnician (user of TeX software), TeXhacker (TeX programmer), TeXmaster (competent TeX programmer), TeXhax, and TeXnique.[61]

Community
TeX Users Group's logo

Notable entities in the TeX community include the TeX Users Group (TUG), which publishes TUGboat and The PracTeX Journal, covering a wide range of topics in digital typography relevant to TeX. The Deutschsprachige Anwendervereinigung TeX (DANTE) is a large user group in Germany. The TeX Users Group was founded in 1980 for educational and scientific purposes, provides an organization for those who have an interest in typography and font design, and are users of the TeX typesetting system invented by Knuth. The TeX Users Group represents the interests of TeX users worldwide. The TeX Users Group publishes the journal TUGboat three times per year;[62] DANTE publishes Die TeXnische Komödie four times per year. Other user groups include DK-TUG in Denmark, GUTenberg in France, GuIT in Italy, and UK-TUG in the United Kingdom; TUG maintains a complete list.[63]


Extensions
gollark: (I'm not sure most of the components have volume settings)
gollark: (or, well, it sort of is, but I never touched a volume setting anywhere in any of it and I can't magically reduce it)
gollark: ABR IS NOT VERY LOUD
gollark: FIX YOUR VOLUME
gollark: Okay.

See also

Notes
  1. Unregistered media type
  2. Although troff still remains as the default formatter of the UNIX documentation.

    References
    1. "Per Bothner (assistant of Knuth) discusses authorship". Knuth definitely wrote most of the code himself, at least for the Metafont re-write, for which I have pe[r]sonal knowledge. However, some of his students (such as Michael Plass and John Hobby) did work on the algorithms used in TeX and Metafont.
    2. Yannis Haralambous. Fonts & Encodings (Translated by P. Scott Horne). Beijing; Sebastopol, Calif: O’Reilly Media, 2007, pp. 235.
    3. "The Definitive, Non-Technical Introduction to LaTeX, Professional Typesetting and Scientific Publishing". Math Vault. 5 September 2015. Retrieved 21 July 2019.
    4. Gaudeul, Alexia (27 March 2006). "Do Open Source Developers Respond to Competition?: The (La)TeX Case Study". SSRN 908946. Cite journal requires |journal= (help)
    5. Knuth, Donald E. "Less brief biography". Don Knuth's Home Page. Retrieved 9 January 2017.
    6. Knuth, Donald. "Commemorative lecture of the Kyoto Prize, 1996" (PDF). Kyoto Prize. Archived from the original (PDF) on 27 January 2018. Retrieved 18 August 2018.
    7. Knuth, Donald Ervin, TEXDR.AFT, archived from the original on 12 January 2015
    8. Knuth and Plass, p. 144
    9. Donald E. Knuth, Knuth meets NTG members, NTG: MAPS. 16 (1996), 38–49. Reprinted as Questions and Answers, III, chapter 33 of Digital Typography, p. 648.
    10. Donald E. Knuth. The New Versions of TeX and METAFONT, TUGboat 10 (1989), 325–328; 11 (1990), 12. Reprinted as chapter 29 of Digital Typography.
    11. "TeX 14 release". Retrieved 20 January 2014.
    12. "What is the future of TeX?". The TeX FAQ. 27 May 2018. Retrieved 21 July 2019.
    13. Donald E. Knuth. The future of TeX and METAFONT, NTG journal MAPS (1990), 489. Reprinted as chapter 30 of Digital Typography, p. 571.
    14. "TeX Engine development". The TeX FAQ. 24 May 2018. Retrieved 21 July 2019.
    15. Donald E. Knuth and Pierre MacKay. Mixing Right-to-Left Texts with Left-to-Right Texts, TUGboat 8 (1987), 14–25. Reprinted as chapter 4 of Digital Typography.
    16. Beebe, p. 10.
    17. Knuth, Donald Ervin; MacKay, Pierre (1987), "Mixing Right-to-Left Texts with Left-to-Right Texts" (PDF), TUGboat, 8: 14–25. Reprinted as "Chapter 4", Digital Typography
    18. Knuth, Donald Ervin (1996), "Questions and Answers I", TUGboat, 17: 7–22. Reprinted as "Chapter 31", Digital Typography, p. 598
    19. Knuth, Donald Ervin (1996), "Questions and Answers II", TUGboat, 17: 355–67. Reprinted as "Chapter 32", Digital Typography, pp. 616–17
    20. Jeffrey, Alan (1990), "Lists in TeX's Mouth" (PDF), TUGboat, 11 (2): 237–45
    21. "CTAN: Package pdftex". ctan.org. Retrieved 21 July 2019.
    22. Knuth 1984, p. 9.
    23. Plain TeX (source code), CTAN
    24. "What are the AMS packages (amsmath, etc.)?". The TeX FAQ. 27 May 2018. Retrieved 21 July 2019.
    25. Knuth 1984, p. 127, Ch. 16: Typing Math Formulas.
    26. Slater, Robert (1989), Portraits in Silicon, MIT Press, p. 349, ISBN 9780262691314
    27. Syropoulos, Apostolos; Tsolomitis, Antonis; Sofroniou, Nick (2003), Digital Typography Using LaTeX, Springer, p. 93, ISBN 9780387952178
    28. Donald E. Knuth. Questions and Answers II, TUGboat 17 (1996), pp. 355–367. Reprinted as chapter 32 of Digital Typography, pp. 620–624.
    29. Donald E. Knuth. Typesetting Concrete Mathematics, TUGboat 10 (1989), pp. 31–36, 342. Reprinted as chapter 18 of Digital Typography, pp. 367–378.
    30. Ulrik Vieth (2001) Math typesetting in TEX: The good, the bad, the ugly
    31. "High-Quality Editing and Display of Mathematical Text in Office 2007".
    32. "LineServices".
    33. "Map" (PDF). www.ntg.nl.
    34. Barnett, Michael P (1965), Computer Typesetting: Experiments and Prospects, Cambridge, MA: MIT Press
    35. Knuth & Plass 1981.
    36. "Donald E. Knuth", TUGboat (interview), Advogato, 21: 103–10, 2000, archived from the original (PDF) on 22 January 2009, retrieved 26 December 2005
    37. "4.1 fmt: Reformat paragraph text", Core GNU utilities (GNU coreutils) manual, GNU Project, 2016
    38. Liang 1983, p. 3.
    39. Liang 1983.
    40. "Appendix H: Hyphenation", The TeXbook, pp. 449–55
    41. Donald E. Knuth, List of updates to the TeX82 listing published in September 1982, available on CTAN.
    42. Donald E. Knuth, Appendix to the Errors of TeX paper, available on CTAN, last modified in January 2003.
    43. Donald E. Knuth. "Knuth: Frequently Asked Questions". www-cs-faculty.stanford.edu/~knuth/. Archived from the original on 6 March 2008. Retrieved 28 November 2019.
    44. Kara Platoni (May–June 2006). "Love at First Byte". Stanford Magazine. Archived from the original on 4 June 2006.
    45. TeX Users Group. "History of TeX". tug.org. Retrieved 28 November 2019.
    46. Donald E. Knuth (2008). "Knuth: Recent News — Financial Fiasco". www-cs-faculty.stanford.edu/~knuth/.
    47. Vim‐LaTex, SourceForge
    48. Automatic TeX plugin, Launch pad
    49. TeX-9, Vim.org
    50. TexMaths Homepage, free.fr
    51. iMath, SourceForge
    52. "The future of TeX and METAFONT", Digital Typography, p. 572
    53. Knuth, Donald E (1986), "Computers and Typesettings" (PDF), TUGboat, 7: 95–98
    54. "Chapter 28", Digital Typography (PDF), p. 560
    55. "Trip", CTAN (TeX) (source code)
    56. Knuth 1986.
    57. Open Source: Technology and Policy by Fadi P. Deek, James A. M. McHugh "Public domain", page 227 (2008)
    58. O'Connell, Heath (2000). "Physicists Thriving with Paperless Publishing". arXiv:physics/0007040.
    59. Donald E. Knuth, The TeXbook, Ch. 1: The Name of the Game, p. 1.
    60. Donald E. Knuth. The TeX Logo in Various Fonts, TUGboat 7 (1986), 101. Reprinted as chapter 6 of Digital Typography.
    61. "The Jargon File—TeX". Retrieved 23 July 2016.
    62. "The Communications of the TeX Users Group". tug.org. TeX Users Group. Retrieved 15 March 2019.
    63. "All TeX User Groups". tug.org. TeX Users Group. Retrieved 17 November 2019.

    Sources
    This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.