Scattering
Atoms or molecules which are exposed to light absorb light energy and re-emit light in different directions with different intensity. This phenomenon is an example of scattering, a general physical process where quanta of some form, such as light, sound, or moving particles, are forced to deviate from a straight trajectory by localized non-uniformities in the medium through which they pass. In conventional use, this also includes deviation of reflected radiation from the angle predicted by the law of reflection. Reflections of radiation that undergoes scattering are often called diffuse reflections and unscattered reflections are called specular (mirror-like) reflections.
| Scattering |
|---|
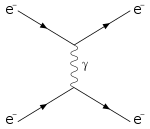 Feynman diagram of scattering between two electrons by emission of a virtual photon |
Scattering may also refer to particle-particle collisions between molecules, atoms, electrons, photons and other particles. Examples include: cosmic ray scattering in the Earth's upper atmosphere; particle collisions inside particle accelerators; electron scattering by gas atoms in fluorescent lamps; and neutron scattering inside nuclear reactors.
The types of non-uniformities which can cause scattering, sometimes known as scatterers or scattering centers, are too numerous to list, but a small sample includes particles, bubbles, droplets, density fluctuations in fluids, crystallites in polycrystalline solids, defects in monocrystalline solids, surface roughness, cells in organisms, and textile fibers in clothing. The effects of such features on the path of almost any type of propagating wave or moving particle can be described in the framework of scattering theory.
Some areas where scattering and scattering theory are significant include radar sensing, medical ultrasound, semiconductor wafer inspection, polymerization process monitoring, acoustic tiling, free-space communications and computer-generated imagery. Particle-particle scattering theory is important in areas such as particle physics, atomic, molecular, and optical physics, nuclear physics and astrophysics. In Particle Physics the quantum interaction and scattering of fundamental particles is described by the Scattering Matrix or S-Matrix, introduced and developed by John Archibald Wheeler and Werner Heisenberg.[1]
Single and multiple scattering

When radiation is only scattered by one localized scattering center, this is called single scattering. It is very common that scattering centers are grouped together; in such cases, radiation may scatter many times, in what is known as multiple scattering. The main difference between the effects of single and multiple scattering is that single scattering can usually be treated as a random phenomenon, whereas multiple scattering, somewhat counterintuitively, can be modeled as a more deterministic process because the combined results of a large number of scattering events tend to average out. Multiple scattering can thus often be modeled well with diffusion theory.
Because the location of a single scattering center is not usually well known relative to the path of the radiation, the outcome, which tends to depend strongly on the exact incoming trajectory, appears random to an observer. This type of scattering would be exemplified by an electron being fired at an atomic nucleus. In this case, the atom's exact position relative to the path of the electron is unknown and would be unmeasurable, so the exact trajectory of the electron after the collision cannot be predicted. Single scattering is therefore often described by probability distributions.
With multiple scattering, the randomness of the interaction tends to be averaged out by a large number of scattering events, so that the final path of the radiation appears to be a deterministic distribution of intensity. This is exemplified by a light beam passing through thick fog. Multiple scattering is highly analogous to diffusion, and the terms multiple scattering and diffusion are interchangeable in many contexts. Optical elements designed to produce multiple scattering are thus known as diffusers. Coherent backscattering, an enhancement of backscattering that occurs when coherent radiation is multiply scattered by a random medium, is usually attributed to weak localization.
Not all single scattering is random, however. A well-controlled laser beam can be exactly positioned to scatter off a microscopic particle with a deterministic outcome, for instance. Such situations are encountered in radar scattering as well, where the targets tend to be macroscopic objects such as people or aircraft.
Similarly, multiple scattering can sometimes have somewhat random outcomes, particularly with coherent radiation. The random fluctuations in the multiply scattered intensity of coherent radiation are called speckles. Speckle also occurs if multiple parts of a coherent wave scatter from different centers. In certain rare circumstances, multiple scattering may only involve a small number of interactions such that the randomness is not completely averaged out. These systems are considered to be some of the most difficult to model accurately.
The description of scattering and the distinction between single and multiple scattering are tightly related to wave–particle duality.
Theory
Scattering theory is a framework for studying and understanding the scattering of waves and particles. Prosaically, wave scattering corresponds to the collision and scattering of a wave with some material object, for instance (sunlight) scattered by rain drops to form a rainbow. Scattering also includes the interaction of billiard balls on a table, the Rutherford scattering (or angle change) of alpha particles by gold nuclei, the Bragg scattering (or diffraction) of electrons and X-rays by a cluster of atoms, and the inelastic scattering of a fission fragment as it traverses a thin foil. More precisely, scattering consists of the study of how solutions of partial differential equations, propagating freely "in the distant past", come together and interact with one another or with a boundary condition, and then propagate away "to the distant future".
Electromagnetics

Electromagnetic waves are one of the best known and most commonly encountered forms of radiation that undergo scattering. Scattering of light and radio waves (especially in radar) is particularly important. Several different aspects of electromagnetic scattering are distinct enough to have conventional names. Major forms of elastic light scattering (involving negligible energy transfer) are Rayleigh scattering and Mie scattering. Inelastic scattering includes Brillouin scattering, Raman scattering, inelastic X-ray scattering and Compton scattering.
Light scattering is one of the two major physical processes that contribute to the visible appearance of most objects, the other being absorption. Surfaces described as white owe their appearance to multiple scattering of light by internal or surface inhomogeneities in the object, for example by the boundaries of transparent microscopic crystals that make up a stone or by the microscopic fibers in a sheet of paper. More generally, the gloss (or lustre or sheen) of the surface is determined by scattering. Highly scattering surfaces are described as being dull or having a matte finish, while the absence of surface scattering leads to a glossy appearance, as with polished metal or stone.
Spectral absorption, the selective absorption of certain colors, determines the color of most objects with some modification by elastic scattering. The apparent blue color of veins in skin is a common example where both spectral absorption and scattering play important and complex roles in the coloration. Light scattering can also create color without absorption, often shades of blue, as with the sky (Rayleigh scattering), the human blue iris, and the feathers of some birds (Prum et al. 1998). However, resonant light scattering in nanoparticles can produce many different highly saturated and vibrant hues, especially when surface plasmon resonance is involved (Roqué et al. 2006).
Models of light scattering can be divided into three domains based on a dimensionless size parameter, α which is defined as:
where πDp is the circumference of a particle and λ is the wavelength of incident radiation. Based on the value of α, these domains are:
- α ≪ 1: Rayleigh scattering (small particle compared to wavelength of light);
- α ≈ 1: Mie scattering (particle about the same size as wavelength of light, valid only for spheres);
- α ≫ 1: geometric scattering (particle much larger than wavelength of light).
Rayleigh scattering is a process in which electromagnetic radiation (including light) is scattered by a small spherical volume of variant refractive indexes, such as a particle, bubble, droplet, or even a density fluctuation. This effect was first modeled successfully by Lord Rayleigh, from whom it gets its name. In order for Rayleigh's model to apply, the sphere must be much smaller in diameter than the wavelength (λ) of the scattered wave; typically the upper limit is taken to be about 1/10 the wavelength. In this size regime, the exact shape of the scattering center is usually not very significant and can often be treated as a sphere of equivalent volume. The inherent scattering that radiation undergoes passing through a pure gas is due to microscopic density fluctuations as the gas molecules move around, which are normally small enough in scale for Rayleigh's model to apply. This scattering mechanism is the primary cause of the blue color of the Earth's sky on a clear day, as the shorter blue wavelengths of sunlight passing overhead are more strongly scattered than the longer red wavelengths according to Rayleigh's famous 1/λ4 relation. Along with absorption, such scattering is a major cause of the attenuation of radiation by the atmosphere. The degree of scattering varies as a function of the ratio of the particle diameter to the wavelength of the radiation, along with many other factors including polarization, angle, and coherence.
For larger diameters, the problem of electromagnetic scattering by spheres was first solved by Gustav Mie, and scattering by spheres larger than the Rayleigh range is therefore usually known as Mie scattering. In the Mie regime, the shape of the scattering center becomes much more significant and the theory only applies well to spheres and, with some modification, spheroids and ellipsoids. Closed-form solutions for scattering by certain other simple shapes exist, but no general closed-form solution is known for arbitrary shapes.
Both Mie and Rayleigh scattering are considered elastic scattering processes, in which the energy (and thus wavelength and frequency) of the light is not substantially changed. However, electromagnetic radiation scattered by moving scattering centers does undergo a Doppler shift, which can be detected and used to measure the velocity of the scattering center/s in forms of techniques such as lidar and radar. This shift involves a slight change in energy.
At values of the ratio of particle diameter to wavelength more than about 10, the laws of geometric optics are mostly sufficient to describe the interaction of light with the particle, and at this point, the interaction is not usually described as scattering.
For modeling of scattering in cases where the Rayleigh and Mie models do not apply such as irregularly shaped particles, there are many numerical methods that can be used. The most common are finite-element methods which solve Maxwell's equations to find the distribution of the scattered electromagnetic field. Sophisticated software packages exist which allow the user to specify the refractive index or indices of the scattering feature in space, creating a 2- or sometimes 3-dimensional model of the structure. For relatively large and complex structures, these models usually require substantial execution times on a computer.
See also
- Bragg diffraction
- Brillouin scattering
- Characteristic mode analysis
- Compton scattering
- Deep scattering layer
- Dynamic Light Scattering
- Espresso crema effect
- Kikuchi line
- Light scattering by particles
- Mie theory
- Mott scattering
- Neutron scattering
- Photon diffusion
- Powder diffraction
- Raman scattering
- Rayleigh scattering
- Rutherford scattering
- Small-angle scattering
- Scattering amplitude
- S-Matrix
- Tyndall effect
- Thomson scattering
- Wolf effect
- X-ray crystallography
References
- Nachtmann, Otto (1990). Elementary Particle Physics: Concepts and Phenomena. Springer-Verlag. pp. 80–93. ISBN 3-540-50496-6.
- "Zodiacal Glow Lightens Paranal Sky". ESO Picture of the Week. European Southern Observatory. Retrieved 2 December 2013.
- Bohren, Craig F.; Donald R. Huffman (1983). Absorption and Scattering of Light by Small Particles. Wiley. ISBN 978-0-471-29340-8.
- Colton, David; Rainer Kress (1998). Inverse Acoustic and Electromagnetic Scattering Theory. Springer. ISBN 978-3-540-62838-5.
- Gonis, Antonios; William H. Butler (1999). Multiple Scattering in Solids. Springer. ISBN 978-0-387-98853-5.
- Prum, Richard O.; Rodolfo H. Torres; Scott Williamson; Jan Dyck (1998). "Coherent light scattering by blue feather barbs". Nature. 396 (6706): 28–29. Bibcode:1998Natur.396...28P. doi:10.1038/23838.
- Roqué, Josep; J. Molera; P. Sciau; E. Pantos; M. Vendrell-Saz (2006). "Copper and silver nanocrystals in lustre lead glazes: development and optical properties". Journal of the European Ceramic Society. 26 (16): 3813–3824. doi:10.1016/j.jeurceramsoc.2005.12.024.
- Seinfeld, John H.; Pandis, Spyros N. (2006). Atmospheric Chemistry and Physics - From Air Pollution to Climate Change (2nd Ed.). John Wiley and Sons, Inc. ISBN 0-471-82857-2
- Stover, John C. (1995). Optical Scattering: Measurement and Analysis. SPIE Optical Engineering Press. ISBN 978-0-8194-1934-7.
External links
| Look up scattering in Wiktionary, the free dictionary. |
| Wikimedia Commons has media related to Scattering. |