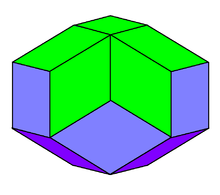
Rhombic icosahedron

The rhombic icosahedron is a polyhedron shaped like an oblate sphere. Its 20 faces are congruent golden rhombi,[1] of which three, four, or five meet at each vertex. It has 5 faces (green on the first figure) meeting at each of its 2 poles (these 2 vertices lie on its axis of (5-fold) symmetry), and 10 faces following its equator (2 of their 4 edges (each) lie on the equator polyline). It has D5d, [2+,10], (2*5) symmetry, order 20.

Rhombic icosahedron
Typezonohedron
Faces20 golden rhombi
Edges40
Vertices22
Faces per vertex3, 4 and 5
Dual polyhedronirregular-faced
pentagonal gyrobicupola
SymmetryD5d, [2+,10], (2*5)
Propertiesconvex, zonohedron

Even though all its faces are congruent, the rhombic icosahedron is not face-transitive, since one may distinguish whether a particular face is near the equator or a pole by examining the types of vertices surrounding that face.

Zonohedron

The rhombic icosahedron is a zonohedron, that is dual to an irregular-faced pentagonal gyrobicupola. It has 5 sets of 8 parallel edges, described as 85 belts.

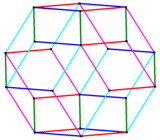The edges of the rhombic icosahedron exist in 5 parallel sets, seen in this wireframe orthogonal projection.

The rhombic icosahedron forms the convex hull of the vertex-first projection of a 5-cube to 3 dimensions. The 32 vertices of a 5-cube map into 22 exterior vertices of the rhombic icosahedron, with the remaining 10 interior vertices forming a pentagonal antiprism. This is the same way one can obtain a Bilinski dodecahedron from a 4-cube and a rhombic triacontahedron from a 6-cube.

The rhombic icosahedron can be derived from the rhombic triacontahedron by removing 10 middle faces.


A rhombic triacontahedron as an elongated rhombic icosahedron
The rhombic icosahedron shares its 5-fold symmetry orthogonal projection with the rhombic triacontahedron
gollark: What convenient timing.
gollark: Yes, says me.
gollark: Wow, love sounds awful.
gollark: There's one bad Rust implementation, one working but VERY limited JS implementation, several experimental bad JS implementations, one decent Nim implementation and actually that's it.
gollark: Even if I constantly dewrote and rewrote it.

References
  1. Weisstein, Eric W. "Rhombic Icosahedron". mathworld.wolfram.com. Retrieved 2019-12-20.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.