Coefficient of relationship

The coefficient of relationship is a measure of the degree of consanguinity (or biological relationship) between two individuals. The term coefficient of relationship was defined by Sewall Wright in 1922, and was derived from his definition of the coefficient of inbreeding of 1921. The measure is most commonly used in genetics and genealogy. A coefficient of inbreeding can be calculated for an individual, and is typically one-half the coefficient of relationship between the parents.

"Relatedness" redirects here. For relatedness in semantics, see Semantic relatedness. For relatedness in psychology, see Self-determination theory.

In general, the higher the level of inbreeding the closer the coefficient of relationship between the parents approaches a value of 1, expressed as a percentage,[lower-alpha 1] and approaches a value of 0 for individuals with arbitrarily remote common ancestors.

Coefficient of relationship

The coefficient of relationship (r) between two individuals B and C is obtained by a summation of coefficients calculated for every line by which they are connected to their common ancestors. Each such line connects the two individuals via a common ancestor, passing through no individual which is not a common ancestor more than once. A path coefficient between an ancestor A and an offspring O separated by n generations is given as:

${\displaystyle p_{AO}=2^{-n}\cdot {\left({\frac {1+f_{A}}{1+f_{O}}}\right)}^{1/2}}$

where f_A and f_O are the coefficients of inbreeding for A and O, respectively.

The coefficient of relationship r_BC is now obtained by summing over all path coefficients:

${\displaystyle r_{BC}=\sum {p_{AB}\cdot p_{AC}}}$

By assuming that the pedigree can be traced back to a sufficiently remote population of perfectly random-bred stock (f_A = 0) the definition of r may be simplified to

${\displaystyle r_{BC}=\sum _{p}{2^{-L(p)}}}$

where p enumerates all paths connecting B and C with unique common ancestors (i.e. all paths terminate at a common ancestor and may not pass through a common ancestor to a common ancestor's ancestor), and L(p) is the length of the path p.

To give an (artificial) example: Assuming that two individuals share the same 32 ancestors of n = 5 generations ago, but do not have any common ancestors at four or fewer generations ago, their coefficient of relationship would be

${\textstyle r=2^{n}\cdot 2^{-2n}=2^{-n}}$, which for n = 5, is, ${\textstyle 2^{-5}={\frac {1}{32}}}$, or approximately 0.0313 or 3%.

Individuals for which the same situation applies for their 1024 ancestors of ten generations ago would have a coefficient of r = 2⁻¹⁰ = 0.1%. If follows that the value of r can be given to an accuracy of a few percent if the family tree of both individuals is known for a depth of five generations, and to an accuracy of a tenth of a percent if the known depth is at least ten generations. The contribution to r from common ancestors of 20 generations ago (corresponding to roughly 500 years in human genealogy, or the contribution from common descent from a medieval population) falls below one part-per-million.

Human relationships

Diagram of common family relationships, where the area of each colored circle is scaled according to the coefficient of relatedness. All relatives of the same relatedness are included together in one of the gray ellipses. Legal degrees of relationship can be found by counting the number of solid-line connections between the self and a relative.[lower-alpha 2]

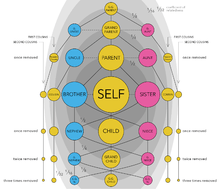
The coefficient of relationship is sometimes used to express degrees of kinship in numeric terms in human genealogy.

In human relationships, the value of the coefficient of relationship is usually calculated based on the knowledge of a full family tree extending to a comparatively small number of generations, perhaps of the order of three or four. As explained above, the value for the coefficient of relationship so calculated is thus a lower bound, with an actual value that may be up to a few percent higher. The value is accurate to within 1% if the full family tree of both individuals is known to a depth of seven generations.[lower-alpha 3]

Degree of relationship	Relationship	Coefficient of relationship (r)
0	identical twins; clones	100%[lower-alpha 4] (1)
1	mother / father / daughter / son [2]	50% (2^−1)
1	parent's identical twin / identical twin's child	50% (2^−1)
2	half-sister / half-brother	25% (2^−2)
2	full sister / full brother	50% (2⋅2^−2)
2	3/4-sister / 3/4-brother	37.5% (2^−2+2^−3)
2	grandmother / grandfather / granddaughter / grandson	25% (2^−2)
3	half-aunt / half-uncle / half-niece / half-nephew	12.5% (2^−3)
3	aunt / uncle / niece / nephew	25% (2⋅2^−3)
4	half-first cousin	6.25% (2^−4)
4	first cousin	12.5% (2⋅2^−4)
4	sesqui-first cousin	18.75% (3⋅2^−4)
4	double-first cousin	25% (4⋅2^−4)
3	great-grandmother / great-grandfather / great-granddaughter / great-grandson	12.5% (2^−3)
4	half-grandaunt / half-granduncle / half-grandniece / half-grandnephew	6.25% (2^−4)
4	grandaunt / granduncle / grandniece / grandnephew	12.5% (2⋅2^−4)
5	half-first cousin once removed	3.125% (2^−5)
5	first cousin once removed	6.25% (2⋅2^−5)
5	sesqui-first cousin once removed	9.375% (3⋅2^−5)
5	double-first cousin once removed	12.5% (4⋅2^−5)
6	half-second cousin	1.5625% (2^−6)
6	second cousin	3.125% (2⋅2^−6)
6	sesqui-second cousin	4.6875% (3⋅2^−6)
6	double-second cousin	6.25% (4⋅2^−6)
6	sester-second cousin	7.8125% (5⋅2^−6)
6	triple-second cousin	9.38% (6⋅2^−6)
6	sesqua-second cousin	10.9375% (7⋅2^−6)
6	quadruple-second cousin	12.5% (8⋅2^−6)
4	great-great-grandmother / great-great-grandfather / great-great-granddaughter / great-great-grandson	6.25% (2^−4)
5	half-great-grandaunt / half-great-granduncle / half-great-grandniece / half-great-grandnephew	3.125% (2^−5)
5	great-grandaunt / great-granduncle / great-grandniece / great-grandnephew	6.25% (2⋅2^−5)
6	half-first cousin twice removed	1.5625% (2^−6)
6	first cousin twice removed	3.125% (2⋅2^−6)
6	sesqui-first cousin twice removed	4.6875% (3⋅2^−6)
6	double-first cousin twice removed	6.25% (4⋅2^−6)
7	half-second cousin once removed	0.78125% (2^−7)
7	second cousin once removed	1.5625% (2⋅2^−7)
7	sesqui-second cousin once removed	2.34375% (3⋅2^−7)
7	double-second cousin once removed	3.125% (4⋅2^−7)
7	sester-second cousin once removed	3.90625% (5⋅2^−7)
7	triple-second cousin once removed	4.6875% (6⋅2^−7)
7	sesqua-second cousin once removed	5.46875% (7⋅2^−7)
7	quadruple-second cousin once removed	6.25% (8⋅2^−7)
8	third cousin	0.78125% (2⋅2^−8)
5	great-great-great-grandmother / great-great-great-grandfather / great-great-great-granddaughter / great-great-great-grandson	3.125% (2^−5)
6	half-great-great-grandaunt / half-great-great-granduncle / half-great-great-grandniece / half-great-great-grandnephew	1.5625% (2^−6)
6	great-great-grandaunt / great-great-granduncle / great-great-grandniece / great-great-grandnephew	3.125% (2⋅2^−6)
7	first cousin thrice removed	1.5625% (2⋅2^−7)
8	second cousin twice removed	0.78125% (2⋅2^−8)
9	third cousin once removed	0.390625% (2⋅2^−9)
10	fourth cousin	0.1953125% (2⋅2^−10)[lower-alpha 5]

Most incest laws concern the relationships where r = 25% or higher, although many ignore the rare case of double first cousins. Some jurisdictions also prohibit sexual relations or marriage between cousins of various degree, or individuals related only through adoption or affinity. Whether there is any likelihood of conception is generally considered irrelevant.

Kinship coefficient

The kinship coefficient is a simple measure of relatedness, defined as the probability that a pair of randomly sampled homologous alleles are identical by descent.[3] More simply, it is the probability that an allele selected randomly from an individual, i, and an allele selected at the same autosomal locus from another individual, j, are identical and from the same ancestor.

Relationship	Kinship coefficient
Individual-self	1/2
full sister / full brother	1/4
mother / father / daughter / son	1/4
grandmother / grandfather / granddaughter / grandson	1/8
aunt / uncle / niece / nephew	1/8
first cousin	1/16
half-sister / half-brother	1/8
Several of the most common family relationships and their corresponding kinship coefficient.

The coefficient of relatedness is equal to twice the kinship coefficient.

Calculation

The kinship coefficient between two individuals, i and j, is represented as Φ_ij. The kinship coefficient between a non-inbred individual and itself, Φ_ii, is equal to 1/2. This is due to the fact that humans are diploid, meaning the only way for the randomly chosen alleles to be identical by descent is if the same allele is chosen twice (probability 1/2). Similarly, the relationship between a parent and a child is found by the chance that the randomly picked allele in the child is from the parent (probability 1/2) and the probability of the allele that is picked from the parent being the same one passed to the child (probability 1/2). Since these two events are independent of each other, they are multiplied Φ_ij = 1/2 X 1/2 = 1/4.[4][5]

See also

• Effective population size
• F-statistics
• Genetic distance
• Malecot's method of coancestry

Notes

1. strictly speaking, r=1 for clones and identical twins, but since the definition of r is usually intended to estimate the suitability of two individuals for breeding, they are typically taken to be of opposite sex.
2. For instance, one's sibling connects to one's parent, which connects to one's self (2 lines) while one's aunt/uncle connects to one's grandparent, which connects to one's parent, which connects to one's self (3 lines).
3. A full family tree of seven generations (128 paths to ancestors of the 7th degree) is unreasonable even for members of high nobility. For example, the family tree of Queen Elizabeth II is fully known for a depth of six generations, but becomes difficult to trace in the seventh generation.
4. By replacement in the definition of the notion of "generation" by "meiosis". Since identical twins are not separated by meiosis, there are no "generations" between them, hence n=0 and r=1. See: [1]
5. This degree of relationship is usually indistinguishable from the relationship to a random individual within the same population (tribe, country, ethnic group).

References

1. genetic-genealogy.co.uk.
2. "Kin Selection". Benjamin/Cummings. Retrieved 2007-11-25.
3. Lange, Kenneth (2003). Mathematical and statistical methods for genetic analysis. Springer. p. 81. ISBN 978-0-387-21750-5.
4. Lange, Kenneth (2003). Mathematical and statistical methods for genetic analysis. Springer. pp. 81–83.
5. Jacquard, Albert (1974). The genetic structure of populations. Springer-Verlag. ISBN 978-3-642-88415-3.

Bibliography

• Wright, Sewall (1921). "Systems of Mating" (PDF). Genetics. 6: 111–178. five papers:
  • I) The biometric relations between offspring and parent
  • II) The effects of inbreeding on the genetic composition of a population
  • III) Assortative mating based on somatic resemblance
  • IV) The effects of selection
  • V) General considerations
• Wright, Sewall (1922). "Coefficients of inbreeding and relationship". American Naturalist. 56 (645): 330–338. doi:10.1086/279872.
• Malécot, G. (1948) Les mathématiques de l’hérédité, Masson et Cie, Paris.
• Lange, K. (1997) Mathematical and statistical methods for genetic analysis, Springer-Verlag, New-York.
• Oliehoek, Pieter; Jack J. Windig; Johan A. M. van Arendonk; Piter Bijma (May 2006). "Estimating Relatedness Between Individuals in General Populations With a Focus on Their Use in Conservation Programs". Genetics. 173: 483–496. doi:10.1534/genetics.105.049940. PMC 1461426. PMID 16510792.