One-dimensional space

In physics and mathematics, a sequence of n numbers can specify a location in n-dimensional space. When n = 1, the set of all such locations is called a one-dimensional space. An example of a one-dimensional space is the number line, where the position of each point on it can be described by a single number.[1]

The number line

In algebraic geometry there are several structures that are technically one-dimensional spaces but referred to in other terms. A field k is a one-dimensional vector space over itself. Similarly, the projective line over k is a one-dimensional space. In particular, if k = ℂ, the complex numbers, then the complex projective line P¹(ℂ) is one-dimensional with respect to ℂ, even though it is also known as the Riemann sphere.

More generally, a ring is a length-one module over itself. Similarly, the projective line over a ring is a one-dimensional space over the ring. In case the ring is an algebra over a field, these spaces are one-dimensional with respect to the algebra, even if the algebra is of higher dimensionality.

Hypersphere

The hypersphere in 1 dimension is a pair of points,[2] sometimes called a 0-sphere as its surface is zero-dimensional. Its length is

${\displaystyle L=2r}$

where ${\displaystyle r}$ is the radius.

Coordinate systems in one-dimensional space

Main article: Coordinate system

One dimensional coordinate systems include the number line and the angle.

• 
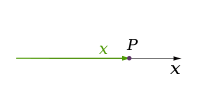  Number line
• 
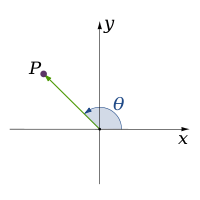  Angle

References

1. Гущин, Д. Д. "Пространство как математическое понятие" (in Russian). fmclass.ru. Retrieved 2015-06-06.
2. Gibilisco, Stan (1983). Understanding Einstein's Theories of Relativity: Man's New Perspective on the Cosmos. TAB Books. p. 89.