Diagonal
In geometry, a diagonal is a line segment joining two vertices of a polygon or polyhedron, when those vertices are not on the same edge. Informally, any sloping line is called diagonal. The word diagonal derives from the ancient Greek διαγώνιος diagonios,[1] "from angle to angle" (from διά- dia-, "through", "across" and γωνία gonia, "angle", related to gony "knee"); it was used by both Strabo[2] and Euclid[3] to refer to a line connecting two vertices of a rhombus or cuboid,[4] and later adopted into Latin as diagonus ("slanting line").
In matrix algebra, a diagonal of a square matrix is a set of entries extending from one corner to the farthest corner.
There are also other, non-mathematical uses.
Non-mathematical uses

In engineering, a diagonal brace is a beam used to brace a rectangular structure (such as scaffolding) to withstand strong forces pushing into it; although called a diagonal, due to practical considerations diagonal braces are often not connected to the corners of the rectangle.
Diagonal pliers are wire-cutting pliers defined by the cutting edges of the jaws intersects the joint rivet at an angle or "on a diagonal", hence the name.
A diagonal lashing is a type of lashing used to bind spars or poles together applied so that the lashings cross over the poles at an angle.
In association football, the diagonal system of control is the method referees and assistant referees use to position themselves in one of the four quadrants of the pitch.

Polygons
As applied to a polygon, a diagonal is a line segment joining any two non-consecutive vertices. Therefore, a quadrilateral has two diagonals, joining opposite pairs of vertices. For any convex polygon, all the diagonals are inside the polygon, but for re-entrant polygons, some diagonals are outside of the polygon.
Any n-sided polygon (n ≥ 3), convex or concave, has diagonals, as each vertex has diagonals to all other vertices except itself and the two adjacent vertices, or n − 3 diagonals, and each diagonal is shared by two vertices.
|
|
|
|
|
Regions formed by diagonals
In a convex polygon, if no three diagonals are concurrent at a single point in the interior, the number of regions that the diagonals divide the interior into is given by
For n-gons with n=3, 4, ... the number of regions is[5]
- 1, 4, 11, 25, 50, 91, 154, 246...
Intersections of diagonals
If no three diagonals of a convex polygon are concurrent at a point in the interior, the number of interior intersections of diagonals is given by .[7][8] This holds, for example, for any regular polygon with an odd number of sides. The formula follows from the fact that each intersection is uniquely determined by the four endpoints of the two intersecting diagonals: the number of intersections is thus the number of combinations of the n vertices four at a time.
Regular polygons
A triangle has no diagonals.
A square has two diagonals of equal length, which intersect at the center of the square. The ratio of a diagonal to a side is
A regular pentagon has five diagonals all of the same length. The ratio of a diagonal to a side is the golden ratio,
A regular hexagon has nine diagonals: the six shorter ones are equal to each other in length; the three longer ones are equal to each other in length and intersect each other at the center of the hexagon. The ratio of a long diagonal to a side is 2, and the ratio of a short diagonal to a side is .
A regular heptagon has 14 diagonals. The seven shorter ones equal each other, and the seven longer ones equal each other. The reciprocal of the side equals the sum of the reciprocals of a short and a long diagonal.
In any regular n-gon with n even, the long diagonals all intersect each other at the polygon's center.
Polyhedrons
A polyhedron (a solid object in three-dimensional space, bounded by two-dimensional faces) may have two different types of diagonals: face diagonals on the various faces, connecting non-adjacent vertices on the same face; and space diagonals, entirely in the interior of the polyhedron (except for the endpoints on the vertices).
Just as a triangle has no diagonals, so also a tetrahedron (with four triangular faces) has no face diagonals and no space diagonals.
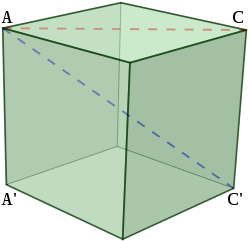
A cuboid has two diagonals on each of the six faces and four space diagonals.
Matrices
In the case of a square matrix, the main or principal diagonal is the diagonal line of entries running from the top-left corner to the bottom-right corner.[9][10][11] For a matrix with row index specified by and column index specified by , these would be entries with . For example, the identity matrix can be defined as having entries of 1 on the main diagonal and zeroes elsewhere:
The top-right to bottom-left diagonal is sometimes described as the minor diagonal or antidiagonal. The off-diagonal entries are those not on the main diagonal. A diagonal matrix is one whose off-diagonal entries are all zero.[12][13]
A superdiagonal entry is one that is directly above and to the right of the main diagonal.[14][15] Just as diagonal entries are those with , the superdiagonal entries are those with . For example, the non-zero entries of the following matrix all lie in the superdiagonal:
Likewise, a subdiagonal entry is one that is directly below and to the left of the main diagonal, that is, an entry with .[16] General matrix diagonals can be specified by an index measured relative to the main diagonal: the main diagonal has ; the superdiagonal has ; the subdiagonal has ; and in general, the -diagonal consists of the entries with .
Geometry
By analogy, the subset of the Cartesian product X×X of any set X with itself, consisting of all pairs (x,x), is called the diagonal, and is the graph of the equality relation on X or equivalently the graph of the identity function from X to x. This plays an important part in geometry; for example, the fixed points of a mapping F from X to itself may be obtained by intersecting the graph of F with the diagonal.
In geometric studies, the idea of intersecting the diagonal with itself is common, not directly, but by perturbing it within an equivalence class. This is related at a deep level with the Euler characteristic and the zeros of vector fields. For example, the circle S1 has Betti numbers 1, 1, 0, 0, 0, and therefore Euler characteristic 0. A geometric way of expressing this is to look at the diagonal on the two-torus S1xS1 and observe that it can move off itself by the small motion (θ, θ) to (θ, θ + ε). In general, the intersection number of the graph of a function with the diagonal may be computed using homology via the Lefschetz fixed point theorem; the self-intersection of the diagonal is the special case of the identity function.
Notes
- Online Etymology Dictionary
- Strabo, Geography 2.1.36–37
- Euclid, Elements book 11, proposition 28
- Euclid, Elements book 11, proposition 38
- Weisstein, Eric W. "Polygon Diagonal." From MathWorld--A Wolfram Web Resource. http://mathworld.wolfram.com/PolygonDiagonal.html
- Sloane, N. J. A. (ed.). "Sequence A006522". The On-Line Encyclopedia of Integer Sequences. OEIS Foundation.
- Poonen, Bjorn; Rubinstein, Michael. "The number of intersection points made by the diagonals of a regular polygon". SIAM J. Discrete Math. 11 (1998), no. 1, 135–156; link to a version on Poonen's website
- , beginning at 2:10
- Bronson (1970, p. 2)
- Herstein (1964, p. 239)
- Nering (1970, p. 38)
- Herstein (1964, p. 239)
- Nering (1970, p. 38)
- Bronson (1970, pp. 203,205)
- Herstein (1964, p. 239)
- Cullen (1966, p. 114)
References
- Bronson, Richard (1970), Matrix Methods: An Introduction, New York: Academic Press, LCCN 70097490
- Cullen, Charles G. (1966), Matrices and Linear Transformations, Reading: Addison-Wesley, LCCN 66021267
- Herstein, I. N. (1964), Topics In Algebra, Waltham: Blaisdell Publishing Company, ISBN 978-1114541016
- Nering, Evar D. (1970), Linear Algebra and Matrix Theory (2nd ed.), New York: Wiley, LCCN 76091646
External links
| Look up diagonal in Wiktionary, the free dictionary. |
- Diagonals of a polygon with interactive animation
- Polygon diagonal from MathWorld.
- Diagonal of a matrix from MathWorld.