Logic optimization

Logic optimization, a part of logic synthesis in electronics, is the process of finding an equivalent representation of the specified logic circuit under one or more specified constraints. Generally the circuit is constrained to minimum chip area meeting a prespecified delay.

Introduction

With the advent of logic synthesis, one of the biggest challenges faced by the electronic design automation (EDA) industry was to find the best netlist representation of the given design description. While two-level logic optimization had long existed in the form of the Quine–McCluskey algorithm, later followed by the Espresso heuristic logic minimizer, the rapidly improving chip densities, and the wide adoption of HDLs for circuit description, formalized the logic optimization domain as it exists today.

Today, logic optimization is divided into various categories:

Based on circuit representation

• Two-level logic optimization
• Multi-level logic optimization

Based on circuit characteristics

• Sequential logic optimization
• Combinational logic optimization

Based on type of execution

• Graphical optimization methods
• Tabular optimization methods
• Algebraic optimization methods

While a two-level circuit representation of circuits strictly refers to the flattened view of the circuit in terms of SOPs (sum-of-products) — which is more applicable to a PLA implementation of the design — a multi-level representation is a more generic view of the circuit in terms of arbitrarily connected SOPs, POSs (product-of-sums), factored form etc. Logic optimization algorithms generally work either on the structural (SOPs, factored form) or functional (BDDs, ADDs) representation of the circuit.

Two-level versus multi-level representations

If we have two functions F₁ and F₂:

${\displaystyle F_{1}=AB+AC+AD,\,}$

${\displaystyle F_{2}=A'B+A'C+A'E.\,}$

The above 2-level representation takes six product terms and 24 transistors in CMOS Rep.

A functionally equivalent representation in multilevel can be:

P = B + C.

F₁ = AP + AD.

F₂ = A'P + A'E.

While the number of levels here is 3, the total number of product terms and literals reduce because of the sharing of the term B + C.

Similarly, we distinguish between sequential and combinational circuits, whose behavior can be described in terms of finite-state machine state tables/diagrams or by Boolean functions and relations respectively.

Circuit minimization in Boolean algebra

In Boolean algebra, circuit minimization is the problem of obtaining the smallest logic circuit (Boolean formula) that represents a given Boolean function or truth table. For the case when the Boolean function is specified by a circuit (that is, we want to find an equivalent circuit of minimum size possible), the unbounded circuit minimization problem was long-conjectured to be ${\displaystyle \Sigma _{2}^{P}}$-complete, a result finally proved in 2008,[1] but there are effective heuristics such as Karnaugh maps and the Quine–McCluskey algorithm that facilitate the process.

Boolean function minimizing methods include:

• Blake–Poretsky method
• Nelson method[2][3][4][5][6]
• Quine method
• Quine–McCluskey method
• method of algebraic transformations
• Petrick's method
• Roth method[7]
• Kudielka method[8][9][10]
• Wells method[11]
• Scheinman's binary method[12][13]
• a method of minimizing functions in bases YES-NO and OR-NOT (Schaeffer and Pierce basis)
• method of undetermined coefficients
• hypercube method
• functional decomposition method
• Espresso heuristic logic minimizer

Purpose

The problem with having a complicated circuit (i.e. one with many elements, such as logic gates) is that each element takes up physical space in its implementation and costs time and money to produce in itself. Circuit minimization may be one form of logic optimization used to reduce the area of complex logic in integrated circuits.

Example

While there are many ways to minimize a circuit, this is an example that minimizes (or simplifies) a Boolean function. Note that the Boolean function carried out by the circuit is directly related to the algebraic expression from which the function is implemented.[14] Consider the circuit used to represent ${\displaystyle (A\wedge {\bar {B}})\vee ({\bar {A}}\wedge B)}$. It is evident that two negations, two conjunctions, and a disjunction are used in this statement. This means that to build the circuit one would need two inverters, two AND gates, and an OR gate.

We can simplify (minimize) the circuit by applying logical identities or using intuition. Since the example states that A is true when B is false or the other way around, we can conclude that this simply means ${\displaystyle A\neq B}$. In terms of logical gates, inequality simply means an XOR gate (exclusive or). Therefore, ${\displaystyle (A\wedge {\bar {B}})\vee ({\bar {A}}\wedge B)\iff A\neq B}$. Then the two circuits shown below are equivalent:

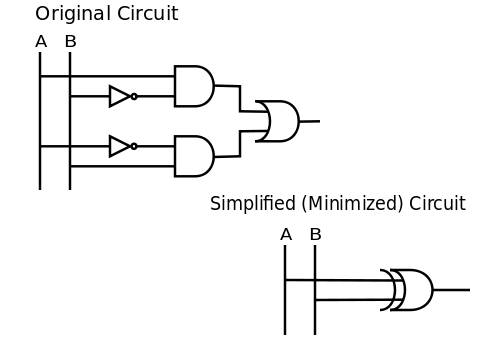
You can additionally check the correctness of the result using a truth table.

Graphical logic minimization methods

Graphical minimization methods for two-level logic include:

• Euler diagram (aka Eulerian circle) (1768) by Leonhard P. Euler (1707–1783)
• Venn diagram (1880) by John Venn (1834–1923)[15][16]
• Marquand diagram (1881) by Allan Marquand (1853–1924)[17][18]
• Harvard minimizing chart (1951) by Howard H. Aiken (1900–1973) and Martha L. Whitehouse of the Harvard Computation Laboratory[19][20][21][22][13]
• Veitch chart (1952) by Edward W. Veitch (1924–2013)[23][18]
• Karnaugh map (1953) by Maurice Karnaugh (1924–)[20][22]
• Contact bones, contact grids (1955), and the triadic map by Antonín Svoboda (1907–1980)[24][25][26][27][28][29][30][31][32][33][34][35][36]
• Graphical method (1957) by Vadim Nikolaevich Roginskij[37] [Вадим Николаевич Рогинский] (1913–1983)[38][39][40][31]
• Händler diagram (aka Mⁿ graph, Händler'scher Kreisgraph, Kreisgraph nach Händler, Händler-Kreisgraph, Händler-Diagramm, Minimisierungsgraph) (1958) by Wolfgang Händler (1920–1998)[41][42][43][35][44][45][46][47][48][49][50][51][52]
• Graph method (1965) by Herbert Kortum (1907–1979)[53][54][55][56][57][58][59][60]
• V diagram (2001) by Jonathan Westphal (1951–)[61][62]
• Majority-inverter graph (MIG) (2014) by Luca Amarú, Pierre-Emmanuel Gaillardon and Giovanni De Micheli[63][64]
• Pandit plot (2017) by Vedhas Pandit and Björn W. Schuller (1975–)[65]

See also

• Binary decision diagram (BDD)
• Circuit minimization
• Prime implicant
• Circuit complexity
• Function composition
• Function decomposition
• Gate underutilization

References

1. Buchfuhrer, David; Umans, Christopher (January 2011). "The complexity of Boolean formula minimization" (PDF). Journal of Computer and System Sciences (JCSS). Computer Science Department, California Institute of Technology, Pasadena, California, USA: Elsevier Inc. 77 (1): 142–153. doi:10.1016/j.jcss.2010.06.011. This is an extended version of the conference paper: Buchfuhrer, David; Umans, Christopher (2008). "The Complexity of Boolean Formula Minimization". Proceedings of Automata, Languages and Programming (PDF). 35th International Colloquium (ICALP). Lecture Notes in Computer Science (LNCS). 5125. Berlin / Heidelberg, Germany: Springer-Verlag. pp. 24–35. doi:10.1007/978-3-540-70575-8_3. ISBN 978-3-540-70574-1. Archived (PDF) from the original on 2018-01-14. Retrieved 2018-01-14.
2. Nelson, Raymond J. (June 1955). "Simplest Normal Truth Functions". Journal of Symbolic Logic. Association for Symbolic Logic. 20 (2): 105–108. doi:10.2307/2266893. JSTOR 2266893. (4 pages) (NB. A method converting a conjunctive normal form into a disjunctive normal form, followed by a procedure similar to Quine's.)
3. Nelson, Raymond J. (September 1955). "Weak Simplest Normal Truth Functions". Journal of Symbolic Logic. Association for Symbolic Logic. 20 (3): 232–234. doi:10.2307/2268219. JSTOR 2268219. (3 pages)
4. Lipp, Hans Martin; Becker, Jürgen (2011). Grundlagen der Digitaltechnik (in German) (reworked 7th ed.). Munich, Germany: Oldenbourg Wissenschaftsverlag GmbH / Walter de Gruyter. ISBN 9783486706932. ISBN 3486706934. Retrieved 2020-05-12. (316 pages)
5. Riznyk, Volodymyr; Solomko, Mykhailo (July 2017). "Minimization of Boolean functions by combinatorial method". Information and Control Systems: Mathematical Modeling (in English and Russian). 4/2 (36): 49–64. doi:10.15587/2312-8372.2017.108532. ISSN 2226-3780. UDC 681.325. Archived (PDF) from the original on 2020-05-12. Retrieved 2020-05-12.
6. Riznyk, Volodymyr; Solomko, Mykhailo (July 2018). "Minimization of Conductive Normal Forms of Boolean Functions by Combinatorial Method" (PDF). Information and Control Systems: Mathematical Modeling (in English and Russian). 5/2 (43): 42–55. doi:10.15587/2312-8372.2018.146312. ISSN 2226-3780. UDC 681.325. Archived (PDF) from the original on 2020-05-12. Retrieved 2020-05-12.
7. Roth, John Paul (November 1960). "Minimization over Boolean Trees". IBM Journal of Research and Development. 4 (5): 543–558. doi:10.1147/rd.45.0543. eISSN 0018-8646. ISSN 0018-8646.
8. Kudielka, Viktor; Walk, Kurt; Bandat, Kurt; Lucas, Peter; Zemanek, Heinrich "Heinz" Josef (1960-02-29). "4–5". In Zemanek, Heinrich "Heinz" Josef (ed.). Programs for Logical Data Processing. Mailüfterl (Final report). Vienna, Austria: Technical University of Vienna, Institut für Nachrichtentechnik. European Reseach Office Contract DA-91-591-EC-1062. Retrieved 2020-05-29. (198 pages)
9. Kudielka, Viktor; Lucas, Peter; Walk, Kurt; Bandat, Kurt; Bekic, Heinz; Zemanek, Heinrich "Heinz" Josef (1961-07-31). "2". Extension of the Algorithmic Language ALGOL (Final Report). European Research Office Contract DA-91–591-EUC-1430.
10. Kudielka, Viktor (January 1963) [1961-10-18]. "Programmierung von Minimisierungsverfahren für zweistufige Logik". In Dörr, Johannes; Peschl, Ernst Ferdinand; Unger, Heinz (eds.). 2. Colloquium über Schaltkreis- und Schaltwerk-Theorie - Vortragsauszüge vom 18. bis 20. Oktober 1961 in Saarbrücken. Internationale Schriftenreihe zur Numerischen Mathematik [International Series of Numerical Mathematics] (ISNM) (in German). 4 (2013-12-20 reprint of 1st ed.). Institut für Angewandte Mathematik, Universität Saarbrücken, Rheinisch-Westfälisches Institut für Instrumentelle Mathematik: Springer Basel AG / Birkhäuser Verlag Basel. pp. 49–65. doi:10.1007/978-3-0348-4156-6. ISBN 978-3-0348-4081-1. Retrieved 2020-04-15. (152 pages)
11. Wells, Mark B. (1962). "Chapter 14. Switching Theory: Application of a Finite Set Covering Theorem to the Simplification of Boolean Function Expressions". Information Processing, Proceedings of the 2nd IFIP Congress 1962, Munich, Germany, August 27 - September 1, 1962. 2. Munich, Germany: North-Holland. pp. 731–735. Retrieved 2020-05-28.
12. Scheinman, Arnold H. (July 1962) [1962-03-06]. "A Method For Simplifying Boolean Functions". Bell System Technical Journal. Nokia Bell Labs. 41 (4): 1337–1346. doi:10.1002/j.1538-7305.1962.tb03280.x. ISSN 0005-8580. (NB. Also known as Scheinman's binary method, this is an easy to use iterative method also for large functions, which will result in significantly simplified functions, but not necessarily in the simplest. The author is sometimes misspelled as "Schienmann".)
13. Föllinger, Otto; Weber, Wolfgang (1967) [June 1965]. "5.4. Die Methode der Harvard Group of Computation / 5.5 Vereinfachungsmethode nach Scheinman". Written at Frankfurt am Main, Germany. Methoden der Schaltalgebra (in German) (1 ed.). Munich, Germany: R. Oldenbourg Verlag. pp. 103, 120, 122–128, 128–135. (6+320+6 pages)
14. Mano, M. Morris; Kime, Charles R. (2014). Logic and Computer Design Fundamentals (4th new international ed.). Pearson Education Limited. p. 54. ISBN 978-1-292-02468-4.
15. Venn, John (July 1880). "I. On the Diagrammatic and Mechanical Representation of Propositions and Reasonings" (PDF). The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science. 5. 10 (59): 1–18. doi:10.1080/14786448008626877. Archived (PDF) from the original on 2017-05-16.
16. Venn, John (1880). "On the employment of geometrical diagrams for the sensible representations of logical propositions". Proceedings of the Cambridge Philosophical Society. 4: 47–59.
17. Marquand, Allan (1881). "XXXIII: On Logical Diagrams for n terms". The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science. 5. 12 (75): 266–270. doi:10.1080/14786448108627104. (NB. Quite many secondary sources erroneously cite this work as "A logical diagram for n terms" or "On a logical diagram for n terms".)
18. Brown, Frank Markham (2012) [2003, 1990]. Boolean Reasoning - The Logic of Boolean Equations (reissue of 2nd ed.). Mineola, New York: Dover Publications, Inc. ISBN 978-0-486-42785-0. ISBN 0-486-42785-4. First Edition PDF
19. Aiken, Howard Hathaway; Blaauw, Gerrit Anne; Burkhart, William; Burns, Robert J.; Cali, Lloyd; Canepa, Michele; Ciampa, Carmela M.; Coolidge, Jr., Charles A.; Fucarile, Joseph R.; Gadd, Jr., J. Orten; Gucker, Frank F.; Harr, John A.; Hawkins, Robert L.; Hayes, Miles V.; Hofheimer, Richard; Hulme, William F.; Jennings, Betty L.; Johnson, Stanley A.; Kalin, Theodore; Kincaid, Marshall; Lucchini, E. Edward; Minty, William; Moore, Benjamin L.; Remmes, Joseph; Rinn, Robert J.; Roche, John W.; Sanbord, Jacquelin; Semon, Warren L.; Singer, Theodore; Smith, Dexter; Smith, Leonard; Strong, Peter F.; Thomas, Helene V.; Wang, An; Whitehouse, Martha L.; Wilkins, Holly B.; Wilkins, Robert E.; Woo, Way Dong; Little, Elbert P.; McDowell, M. Scudder (1952) [January 1951]. "Chapter V: Minimizing charts". Synthesis of electronic computing and control circuits. The Annals of the Computation Laboratory of Harvard University. XXVII (second printing, revised ed.). Write-Patterson Air Force Base: Harvard University Press (Cambridge, Massachusetts, USA) / Geoffrey Cumberlege Oxford University Press (London). pp. preface, 50–67. Retrieved 2017-04-16. […] Martha Whitehouse constructed the minimizing charts used so profusely throughout this book, and in addition prepared minimizing charts of seven and eight variables for experimental purposes. […] Hence, the present writer is obliged to record that the general algebraic approach, the switching function, the vacuum-tube operator, and the minimizing chart are his proposals, and that he is responsible for their inclusion herein. […] (2+x+278+2 pages) (NB. Work commenced in April 1948.)
20. Karnaugh, Maurice (November 1953) [1953-04-23, 1953-03-17]. "The Map Method for Synthesis of Combinational Logic Circuits" (PDF). Transactions of the American Institute of Electrical Engineers, Part I: Communication and Electronics. 72 (5): 593–599. doi:10.1109/TCE.1953.6371932. Paper 53-217. Archived from the original (PDF) on 2017-04-16. Retrieved 2017-04-16.
21. Phister, Jr., Montgomery (April 1959) [December 1958]. Logical design of digital computers. Digital Design and Applications (3rd printing, 1st ed.). New York, USA: John Wiley & Sons Inc. pp. 75–83. ISBN 0-47168805-3. LCCN 58-6082. MR 0093930. ISBN 978-0-47168805-1. (xvi+408 pages)
22. Curtis, H. Allen (1962). A new approach to the design of switching circuits. The Bell Laboratories Series. Princeton, New Jersey, USA: D. van Nostrand Company, Inc.
23. Veitch, Edward Westbrook (1952-05-03) [1952-05-02]. "A Chart Method for Simplifying Truth Functions". Transactions of the 1952 ACM Annual Meeting. ACM Annual Conference/Annual Meeting: Proceedings of the 1952 ACM Annual Meeting (Pittsburgh, Pennsylvania, USA). New York, USA: Association for Computing Machinery (ACM): 127–133. doi:10.1145/609784.609801.
24. Svoboda, Antonín (1955-11-27) [1955-11-22]. Graphisch-mechanische Hilfsmittel für die Synthese von Relaisschaltungen [Graphical-mechanical aids for the synthesis of relay circuits] (Report). Dresden, Germany: Internationales Mathematiker-Kolloquium über aktuelle Probleme der Rechentechnik. pp. 43–50. (NB. According to Constantinescu the contents might be identical to a journal article in 1956.)
25. Svoboda, Antonín (1956a). Graficko-mechanické pomůcky užívané při analyse a synthese kontaktových obvodů [Utilization of graphical-mechanical aids for the analysis and synthesis of contact circuits]. Stroje na zpracování informací [Symposium on information processing machines] (in Czech). IV. Prague: Czechoslovak Academy of Sciences, Research Institute of Mathematical Machines. pp. 9–22.
26. Svoboda, Antonín (1956b). (unknown) [Graphical-Mechanical Aids for the Synthesis of Relay Circuits]. Nachrichtentechnische Fachberichte (NTF), Beihefte der Nachrichtentechnischen Zeitschrift (NTZ) (in Czech). 4. Braunschweig, Germany: Friedrich Vieweg & Sohn. pp. 213–218. ECIP55 213. (NB. According to Constantinescu the contents might be identical to a congress report in 1955.)
27. Svoboda, Antonín (1959) [1957-03-29]. "Some Applications of Contact Grids". Proceedings of an International Symposium on the Theory of Switching, 2–5 April 1957, Part I. The Annals of the Computation Laboratory of Harvard University. XXIX. Harvard University, Cambridge, Massachusetts, USA: Harvard University Press. pp. 293–305. (305 pages)
28. Svoboda, Antonín (1958). (unknown) [Graphical aids to minimization in switching circuits]. Stroje na zpracování informací [Symposium on information processing machines] (in Czech). VI. Prague: Czechoslovak Academy of Sciences, Research Institute of Mathematical Machines. pp. 35–53.
29. McNaughton, Robert Forbes (March 1958). "Antonin Svoboda. Graphico-mechanical aids for the synthesis of relay circuits. Aktuelle Probleme der Rechentechnik, Deutscher Verlag der Wissenschaften, Berlin 1957, pp. 43–50". Journal of Symbolic Logic (Review). 23 (1): 60–61. doi:10.2307/2964502. Retrieved 2020-05-14. The two graphico-mechanical aids are contact bones and contact grids. Contact bones are an aid in analyzing (i.e., finding a logical formula for) contact networks. The logical theory of contact network analysis has been generally understood for a long time, but there are practical difficulties, especially in the analysis of bridge networks (i.e., networks which are not of the series-parallel type). Contact grids are an aid in obtaining a normal formula for functions given in truth-table form. They are helpful in obtaining what are called (by others) prime implicants. […] (NB. This review is about Svoboda's congress report.)
30. Constantinescu, Paul (1959-12-22). "Svoboda, Antonin. Graphical-mechanical aids for the synthesis of relay circuits. Elektronische Rechenmaschinen und Informationsverarbeitung, 213–218 (1956). — Ber. Internat. Math.-Kolloquium Dresden, 22. bis 27. Nov. 1955, 42–50 (1957)". Zentralblatt für Mathematik (Review). 82 (1): 126. Zbl 0082.12602. Archived from the original on 2020-05-14. Retrieved 2020-05-14. The author utilizes interesting mechanical aids in solving problems concerning contact networks. The basis for the creation of these aids is the fact that each independent variable may be expressed by a Boolean sum of variables which define the state of the network. Employing "contact bones" and "contact grids" the author achieves the analysis and synthesis of a contact network and the transformation of the Boolean functions given in tabular form in algebraic form. (NB. This review is about Svoboda's congress report and journal article.)
31. Roginskij [Рогинский], Vadim Nikolaevich [Вадим Николаевич] (1962). Grundlagen der Struktursynthese von Relaisschaltungen (in German). Translated by Hausenblas, Albin; Pfaffinger, Robert; Resele, H. (1st German ed.). Munich, Germany: R. Oldenbourg Verlag. OCLC 968499019. OCLC 163791522. Retrieved 2002-05-30 (204 pages). This book is a translation of the original work: Roginskij [Рогинский], Vadim Nikolaevich [Вадим Николаевич] (1959). Kharkevich [Харкевич], Aleksandr Aleksandrovich [Александр Александрович] (ed.). Ėlementy strukturnogo sinteza releĭnykh skhem upravlenii︠a︡ Элементы структурного синтеза релейных схем управления (in Russian) (1st ed.). Moscow: Изд-во Академии наук СССР (Izdatel'stvo akademii nauk SSSR). Also available in English as: Roginskij [Рогинский], Vadim Nikolaevich [Вадим Николаевич] (1963). The synthesis of relay switching circuits. Translated by Chrzczonowicz (1st English ed.). New York, USA: Van Nostrand Reinhold Inc. ISBN 0-44207020-9. (188 pages).
32. Svoboda, Antonín (1960). Analysis of Boolean functions by logical punched-cards. Stroje na zpracování informací [Symposium on information processing machines]. VII. pp. 13–20.
33. Svoboda [Свобода], Antonín [Антони́н] (1961-02-02). Некоторые способы применения контактных сеток [Some applications of contact grids] (PDF). Avtomatika i Telemekhanika Автоматика и Телемеханика [Automation and Remote Control] (in Russian). XXII (8): 1061–1107. Mi at12365. Retrieved 2020-05-16. (11 pages)
34. Svoboda, Antonín (December 1969). "Logical Instruments for Teaching Logical Design". IEEE Transactions on Education. IEEE. E-12 (4): 262–273. doi:10.1109/TE.1969.4320517. eISSN 1557-9638. ISSN 0018-9359.
35. Steinbuch, Karl W.; Weber, Wolfgang; Heinemann, Traute, eds. (1974) [1967]. Taschenbuch der Informatik - Band II - Struktur und Programmierung von EDV-Systemen. Taschenbuch der Nachrichtenverarbeitung (in German). 2 (3 ed.). Berlin, Germany: Springer-Verlag. pp. 25, 62, 96, 122–123, 238. ISBN 3-540-06241-6. LCCN 73-80607.
36. Svoboda, Antonín; White, Donnamaie E. (2016) [2012, 1985, 1979-08-01]. Advanced Logical Circuit Design Techniques (PDF) (retyped electronic reissue ed.). Garland STPM Press (original issue) / WhitePubs Enterprises, Inc. (reissue). ISBN 0-8240-7014-3. LCCN 78-31384. ISBN 978-0-8240-7014-4. Archived (PDF) from the original on 2016-03-15. Retrieved 2017-04-15.
37. Вадим Николаевич Рогинский (некролог) [Vadim Nikolaevich Roginsky (obituary)]. Problemy Peredachi Informatsii Проблемы передачи информации [Problems of Information Transmission] (in Russian). XIX (3): 111. 1983. ISSN 0555-2923. Mi ppi1195. Retrieved 2020-05-29. (NB. The author's name is sometimes translated as "Vladimir Nikolaevič", "Wladimir Nikolajewitsch" and as "Roginsky", "Roginskiĭ", or "Roginski".)
38. Roginskij [Рогинский], Vadim Nikolaevich [Вадим Николаевич] (1957). "(unknown)" [Graphical method of synthesizing contact networks]. Èlektrosvâzʹ (in Russian). XI (11): 82–88. ISSN 0013-5771.
39. Roginskij [Рогинский], Vadim Nikolaevich [Вадим Николаевич] (1959) [1957-03-29]. "A graphical method for the synthesis of multi-terminal contact networks". Proceedings of an International Symposium on the Theory of Switching, 2–5 April 1957, Part II. The Annals of the Computation Laboratory of Harvard University. XXX. Harvard University, Cambridge, Massachusetts, USA. pp. 302–315. (345 pages) (NB. This is a translation of a Russian paper prepared for the symposium. Roginskij submitted the paper for presentation, but then could not attend personally. The translation was carried out by some of the American attendees.)
40. Roginskij [Рогинский], Vadim Nikolaevich [Вадим Николаевич] (1958). Povarov [Поваров], Gellius Nikolaevich [Геллий Николаевич] (ed.). "(unknown)" [Graphical method for synthesizing multi-terminal contact networks]. Avtomatika [Automation] (in Russian). Kiev. 3: 84–91. ISSN 0572-2691.
41. Händler, Wolfgang (1958). Ein Minimisierungsverfahren zur Synthese von Schaltkreisen (Minimisierungsgraphen) (Dissertation) (in German). Potsdam, Germany: Technische Hochschule Darmstadt. D 17. (73 pages+app.)
42. Händler, Wolfgang (2013) [June 1961, 1960-10-26]. "Zum Gebrauch von Graphen in der Schaltkreis- und Schaltwerktheorie". In Peschl, Ernst Ferdinand; Unger, Heinz (eds.). Colloquium über Schaltkreis- und Schaltwerk-Theorie - Vortragsauszüge vom 26. bis 28. Oktober 1960 in Bonn. Internationale Schriftenreihe zur Numerischen Mathematik [International Series of Numerical Mathematics] (ISNM) (in German). 3. Institut für Angewandte Mathematik, Universität Saarbrücken, Rheinisch-Westfälisches Institut für Instrumentelle Mathematik: Springer Basel AG / Birkhäuser Verlag Basel. pp. 169–198. doi:10.1007/978-3-0348-5770-3_10. ISBN 978-3-0348-5771-0. ISBN 3-0348-5771-3. (198 pages)
43. Berger, Erich R.; Händler, Wolfgang (1967) [1962]. Steinbuch, Karl W.; Wagner, Siegfried W. (eds.). Taschenbuch der Nachrichtenverarbeitung (in German) (2 ed.). Berlin, Germany: Springer-Verlag OHG. pp. 64, 1034–1035, 1036, 1038. LCCN 67-21079. Title No. 1036. […] Übersichtlich ist die Darstellung nach Händler, die sämtliche Punkte, numeriert nach dem Gray-Code […], auf dem Umfeld eines Kreises anordnet. Sie erfordert allerdings sehr viel Platz. […] [Händler's illustration, where all points, numbered according to the Gray code, are arranged on the circumference of a circle, is easily comprehensible. It needs, however, a lot of space.]
44. Dokter, Folkert; Steinhauer, Jürgen (1973-06-18). "3.7.1. Händler's diagram". Digital Electronics. Philips Technical Library (PTL) / Macmillan Education (Reprint of 1st English ed.). Eindhoven, Netherlands: The Macmillan Press Ltd. / N. V. Philips' Gloeilampenfabrieken. pp. 108–111. doi:10.1007/978-1-349-01417-0. ISBN 978-1-349-01419-4. SBN 333-13360-9. Retrieved 2020-05-11. (270 pages) (NB. This is based on a translation of volume I of the two-volume German edition.)
45. Dokter, Folkert; Steinhauer, Jürgen (1975) [1969]. "3.7.1. Kreisgraphen nach Händler". Digitale Elektronik in der Meßtechnik und Datenverarbeitung: Theoretische Grundlagen und Schaltungstechnik. Philips Fachbücher (in German). I (improved and extended 5th ed.). Hamburg, Germany: Deutsche Philips GmbH. pp. 115, 124, 129, 130–134 [130–134]. ISBN 3-87145-272-6. (xii+327+3 pages) (NB. The German edition of volume I was published in 1969, 1971, two editions in 1972, and 1975. Volume II was published in 1970, 1972, 1973, and 1975.)
46. Klar, Rainer (1970-02-01). "2.4.2 Graphische Minimisierungsverfahren" [2.4.2 Graphical minimisation methods]. Digitale Rechenautomaten – Eine Einführung [Digital Computers – An Introduction]. Sammlung Göschen (in German). 1241/1241a (1 ed.). Berlin, Germany: Walter de Gruyter & Co. / G. J. Göschen'sche Verlagsbuchhandlung. pp. 70–73. ISBN 3-11-083160-0. ISBN 978-3-11-083160-3. Archiv-Nr. 7990709. Archived from the original on 2020-04-13. Retrieved 2020-04-13. […] Der Kreisgraph nach Händler ordnet den einzelnen Mintermen Knoten eines Graphen zu. Die Nachbarschaft von Mintermen wird durch Kanten dargestellt, die die entsprechenden Knoten miteinander verbinden. Bei dem "Kreisgraph" liegen sämtliche Knoten auf einem Kreis. Um symmetrische Kanten zu bekommen, wird die Reihenfolge der Knoten (bzw. Minterme) durch den reflektierten Gray-Code festgelegt, der sich durch fortlaufende Spiegelung und Ergänzung konstruieren läßt. Die negierten Variablen werden dabei durch Nullen, die nichtnegierten durch Einsen dargestellt. Man beginnt mit einer Variablen, die negiert (0) oder nichtnegiert (1) auftritt. Die 0 und 1 werden gespiegelt. Durch Anfügen einer Null vor 0 und 1 und einer Eins vor die Spiegelbilder werden Terme mit 2 Variablen gebildet. Die Spiegelung und das Anfügen von Nullen und Einsen wird wiederholt, bis die gewünschte Zahl von n Variablen und 2ⁿ Termen erreicht ist. […] Das Minimisierungsverfahren mit dem Kreisgraphen verläuft in folgenden Schritten: I. Aufstellung der DKF [disjunktive kanonische Form]. II. Alle Knoten, die auftretende Minterme repräsentieren, werden gekennzeichnet. III. Alle Kanten, die markierte Knoten verbinden, werden gekennzeichnet. Der so entstandene Untergraph markiert sämtliche Primimplikanten. Er setzt sich zusammen aus folgenden Unterstrukturen: isolierten Knoten (Primimplikant der Länge n), 2¹ verbundenen Knoten (Primimplikant der Länge n-1), 2² verbundenen Knoten (Primimplikant der Länge n-2), 2³ verbundenen Knoten (Primimplikant der Länge n-3) usw. Das Auffinden der wesentlichen Primimplikanten und der Restüberdeckung bleibt wie beim Karnaugh-Veitch-Diagramm der Geschicklichkeit überlassen. […] (205 pages) (NB. A 2019 reprint of the first edition is available under ISBN 3-11002793-3, 978-3-11002793-8. A reworked and expanded 4th edition exists as well.)
47. Klar, Rainer (1989) [1988-10-01]. "2.4.2 Graphische Minimisierungsverfahren" [2.4.2 Graphical minimisation methods]. Digitale Rechenautomaten – Eine Einführung in die Struktur von Computerhardware [Digital Computers – An Introduction into the structure of computer hardware]. Sammlung Göschen (in German). 2050 (4th reworked ed.). Berlin, Germany: Walter de Gruyter & Co. pp. 94–97. ISBN 3-11011700-2. ISBN 978-3-11011700-4. (320 pages)
48. Hotz, Günter (1974). Schaltkreistheorie [Switching circuit theory]. DeGruyter Lehrbuch (in German) (1 ed.). Walter de Gruyter & Co. p. 117. ISBN 3-11-00-2050-5. Archived from the original on 2020-04-13. Retrieved 2020-04-13. […] Der Kreisgraph von Händler ist für das Auffinden von Primimplikanten gut brauchbar. Er hat den Nachteil, daß er schwierig zu zeichnen ist. Diesen Nachteil kann man allerdings durch die Verwendung von Schablonen verringern. […] [The circle graph by Händler is well suited to find prime implicants. A disadvantage is that it is difficult to draw. This can be remedied using stencils.]
49. "Informatik Sammlung Erlangen (ISER)" (in German). Erlangen, Germany: Friedrich-Alexander Universität. 2012-03-13. Archived from the original on 2017-05-16. Retrieved 2017-04-12. (NB. Shows a picture of a Kreisgraph by Händler.)
50. "Informatik Sammlung Erlangen (ISER) - Impressum" (in German). Erlangen, Germany: Friedrich-Alexander Universität. 2012-03-13. Archived from the original on 2012-02-26. Retrieved 2017-04-15. (NB. Shows a picture of a Kreisgraph by Händler.)
51. Zemanek, Heinrich "Heinz" Josef (2013) [1990]. "Geschichte der Schaltalgebra" [History of circuit switching algebra]. In Broy, Manfred (ed.). Informatik und Mathematik [Computer Sciences and Mathematics] (in German). Springer-Verlag. pp. 43–72. doi:10.1007/978-3-642-76677-0_3. ISBN 9783642766770. ISBN 3642766773. Einen Weg besonderer Art, der damals zu wenig beachtet wurde, wies W. Händler in seiner Dissertation […] mit einem Kreisdiagramm. […] (NB. Collection of papers at a colloquium held at the Bayerische Akademie der Wissenschaften, 1989-06-12/14, in honor of Friedrich L. Bauer.)
52. Bauer, Friedrich Ludwig; Wirsing, Martin (March 1991). Elementare Aussagenlogik (in German). Berlin / Heidelberg: Springer-Verlag. pp. 54–56, 71, 112–113, 138–139. ISBN 3-540-52974-8. ISBN 978-3-540-52974-3. […] handelt es sich um ein Händler-Diagramm […], mit den Würfelecken als Ecken eines 2^m-gons. […] Abb. […] zeigt auch Gegenstücke für andere Dimensionen. Durch waagerechte Linien sind dabei Tupel verbunden, die sich nur in der ersten Komponente unterscheiden; durch senkrechte Linien solche, die sich nur in der zweiten Komponente unterscheiden; durch 45°-Linien und 135°-Linien solche, die sich nur in der dritten Komponente unterscheiden usw. Als Nachteil der Händler-Diagramme wird angeführt, daß sie viel Platz beanspruchen. […]
53. Kortum, Herbert (1965). "Minimierung von Kontaktschaltungen durch Kombination von Kürzungsverfahren und Graphenmethoden" [Minimization of contact circuits by combination of reduction procedures and graphical methods]. messen-steuern-regeln (msr) (in German). Berlin / Leipzig, Germany: VEB Verlag Technik. 8 (12): 421–425. ISSN 0026-0347. CODEN MSRGAN.
54. Kortum, Herbert (1966). "Konstruktion und Minimierung von Halbleiterschaltnetzwerken mittels Graphentransformation". messen-steuern-regeln (msr) (in German). Berlin / Leipzig, Germany: VEB Verlag Technik. 9 (1): 9–12. ISSN 0026-0347. CODEN MSRGAN.
55. Kortum, Herbert (1966). "Weitere Bemerkungen zur Minimierung von Schaltnetzwerken mittels Graphenmethoden". messen-steuern-regeln (msr) (in German). Berlin / Leipzig, Germany: VEB Verlag Technik. 9 (3): 96–102. ISSN 0026-0347. CODEN MSRGAN.
56. Kortum, Herbert (1966). "Weitere Bemerkungen zur Behandlung von Schaltnetzwerken mittels Graphen. Konstruktion von vermaschten Netzwerken (Brückenschaltungen)" [Further remarks on treatment of switching networks by means of graphs]. messen-steuern-regeln (msr) (in German). Berlin / Leipzig, Germany: VEB Verlag Technik. 9 (5): 151–157. ISSN 0026-0347. CODEN MSRGAN; Kortum, Herbert (1965). "Weitere Bemerkungen zur Behandlung von Schaltnetzwerken mittels Graphen" [Further remarks on treatment of switching networks by means of graphs]. Regelungstechnik (in German). 10. Internationales Wissenschaftliches Kolloquium, Ilmenau. Technische Hochschule. 10 (5): 33–39.
57. Kortum, Herbert (1967). "Über zweckmäßige Anpassung der Graphenstruktur diskreter Systeme an vorgegebene Aufgabenstellungen". messen-steuern-regeln (msr) (in German). Berlin / Leipzig, Germany: VEB Verlag Technik. 10 (6): 208–211. ISSN 0026-0347. CODEN MSRGAN.
58. Kortum, Herbert (1966) [1965]. "Zur Minimierung von Schaltsystemen" [Minimization of switching circuits]. Wissenschaftliche Zeitschrift der TU Ilmenau (in German). Jena, Germany: Technische Hochschule für Elektrotechnik Ilmenau / Forschungsstelle für Meßtechnik und Automatisierung der Deutschen Akademie der Wissenschaften. 12 (2): 181–186.
59. Tafel, Hans Jörg (1971). "4.3.5. Graphenmethode zur Vereinfachung von Schaltfunktionen". Written at RWTH, Aachen, Germany. Einführung in die digitale Datenverarbeitung [Introduction to digital information processing] (in German). Munich, Germany: Carl Hanser Verlag. pp. 98–105, 107–113. ISBN 3-446-10569-7.
60. Axmann, Hans-Peter (2019) [1979-06-13]. Einführung in die technische Informatik: Funktionsweise digitaler Bausteine und deren Verwendung in Datenerfassungssystemen (in German) (reprint of 1st ed.). Springer-Verlag Wien GmbH. p. 37. doi:10.1007/978-3-7091-4478-7. ISBN 978-3-211-81546-5. Retrieved 2020-04-15. […] Die Graphenmethode zur Vereinfachung von Schaltfunktionen zeichnet sich durch besondere Anschaulichkeit und Einfachheit aus. Sie ist dann besonders vorteilhaft, wenn die Schaltfunktion unter Verwendung bestimmter Verknüpfungsglieder mit minimalem Aufwand an Bauelementen und Verbindungsleitungen zu realisieren ist. Sie ist anderen Methoden, besonders bei der Netzwerksynthese von Brückenschaltungen wie auch bei der Optimierung von Kontaktschaltungen mit Sperrdioden, überlegen. Die erfolgreiche Anwendung der Graphenmethode setzt voraus, daß die vorgegebene Funktion bereits in einer weitgehend vereinfachten Form vorliegt, da mit dieser Methode Redundanzen nur noch sehr schwer zu eliminieren sind. […] (290 pages)
61. Westphal, Jonathan (2007-08-07) [2001-10-05, 2000-10-06]. "Devices and techniques for logical processing" (PDF). Patent US7254304B2. Archived (PDF) from the original on 2020-05-09. Retrieved 2020-05-09. (77 pages)
62. Westphal, Jonathan; Hardy, Jim (2005-10-01) [2004-02-16]. "Logic as a Vector System". Journal of Logic and Computation. Idaho State University, Pocatello, Idaho, USA: Oxford University Press. 15 (5): 751–765. doi:10.1093/logcom/exi040. Archived from the original on 2020-05-09. Retrieved 2020-05-09. (15 pages)
63. Amarú, Luca; Gaillardon, Pierre-Emmanuel; De Micheli, Giovanni (2014-05-05) [2014-05-01]. Written at Switzerland. "Majority-Inverter Graph: A Novel Data-Structure and Algorithms for Efficient Logic Optimization". Proceedings of the 51st Annual Design Automation Conference (DAC). San Francisco, California, USA: Association for Computing Machinery (ACM): 1–6. doi:10.1145/2593069.2593158. Archived from the original on 2020-05-09. Retrieved 2020-05-09. (6 pages)
64. Amarú, Luca; Gaillardon, Pierre-Emmanuel; De Micheli, Giovanni (2016). Written at Switzerland. "Majority-Inverter Graph: A novel data-structure and algorithms for efficient logic optimization". IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems. San Francisco, California, USA: IEEE. 35 (5): 806–819. doi:10.1145/2593069.2593158. ISBN 978-1-4799-3017-3. ISSN 0738-100X. Retrieved 2020-05-09. (14 pages)
65. Pandit, Vedhas; Schuller, Björn Wolfgang (2017-12-31) [2017-11-14, 2017-10-11, 2017-05-05]. Scarpiniti, Michele (ed.). "A Novel Graphical Technique for Combinational Logic Representation and Optimization" (PDF). Complexity. Hindawi Publishing Corporation / John Wiley & Sons, Inc. 2017 (5): 1–12. doi:10.1155/2017/9696342. eISSN 1099-0526. ISSN 1076-2787. Article ID 9696342. Archived (PDF) from the original on 2020-05-09. Retrieved 2020-05-09. (12 pages)

Further reading

• Hwa, "Sherman" Hsuen Ren (June 1974). "A Method of Generating Prime Implicants of a Boolean Expression". IEEE Transactions on Computers. IEEE. C-23 (6): 637–641. doi:10.1109/T-C.1974.224003. eISSN 1557-9956. ISSN 0018-9340. S2CID 10646917. 1F09. Retrieved 2020-05-12; Hwa, "Sherman" Hsuen Ren (April 1973). A Method of Generating Prime Implicants of a Boolean Expression. Basser Department of Computer Science, University of Sydney. Technical Report 82.
• Lind, Larry Frederick; Nelson, John Christopher Cunliffe (1977). Analysis and Design of Sequential Digital Systems. Macmillan Press. ISBN 0-33319266-4. (146 pages)
• Ghosh, Debidas (June 1977) [1977-01-21]. "A method of generating prime factors of a Boolean Expression in a conjunctive normal form with the possibility of inclusion of Don't care combination" (PDF). Journal of Technology. Department of Mathematics, Bengal Engineering College, Howrah, India. XXII (1). Archived (PDF) from the original on 2020-05-12. Retrieved 2020-05-12.
• De Micheli, Giovanni (1994). Synthesis and Optimization of Digital Circuits. McGraw-Hill. ISBN 0-07-016333-2. (NB. Chapters 7–9 cover combinatorial two-level, combinatorial multi-level, and respectively sequential circuit optimization.)
• Hachtel, Gary D.; Somenzi, Fabio (2006) [1996]. Logic Synthesis and Verification Algorithms. Springer Science & Business Media. ISBN 978-0-387-31005-3.
• Kohavi, Zvi; Jha, Niraj K. (2009). "4–6". Switching and Finite Automata Theory (3rd ed.). Cambridge University Press. ISBN 978-0-521-85748-2.
• Knuth, Donald Ervin (2010). "7.1.2: Boolean Evaluation". The Art of Computer Programming. 4A. Addison-Wesley. pp. 96–133. ISBN 978-0-201-03804-0.
• Rutenbar, Rob A. Multi-level minimization, Part I: Models & Methods (PDF) (lecture slides). Carnegie Mellon University (CMU). Lecture 7. Archived (PDF) from the original on 2018-01-15. Retrieved 2018-01-15; Rutenbar, Rob A. Multi-level minimization, Part II: Cube/Cokernel Extract (PDF) (lecture slides). Carnegie Mellon University (CMU). Lecture 8. Archived (PDF) from the original on 2018-01-15. Retrieved 2018-01-15.
• Tomaszewski, Sebastian P.; Celik, Ilgaz U.; Antoniou, George E. (December 2003) [2003-03-05, 2002-04-09]. ""WWW-based Boolean function minimization" (PDF). International Journal of Applied Mathematics and Computer Science. 13 (4): 577–584. Archived (PDF) from the original on 2020-05-10. Retrieved 2020-05-10. (7 pages)
• Wilhelmy, Alexander; Kudielka, Viktor; Deussen, Peter; Böhling, Karl Heinz; Händler, Wolfgang; Neander, Joachim (January 1963) [1961-10-18]. Dörr, Johannes; Peschl, Ernst Ferdinand; Unger, Heinz (eds.). 2. Colloquium über Schaltkreis- und Schaltwerk-Theorie - Vortragsauszüge vom 18. bis 20. Oktober 1961 in Saarbrücken. Internationale Schriftenreihe zur Numerischen Mathematik [International Series of Numerical Mathematics] (ISNM) (in German). 4 (2013-12-20 reprint of 1st ed.). Institut für Angewandte Mathematik, Universität Saarbrücken, Rheinisch-Westfälisches Institut für Instrumentelle Mathematik: Springer Basel AG / Birkhäuser Verlag Basel. doi:10.1007/978-3-0348-4156-6. ISBN 978-3-0348-4081-1. Retrieved 2020-04-15. (152 pages)
• Brayton, Robert King; Rudell, Richard L.; Sangiovanni-Vincentelli, Alberto Luigi; Wang, Albert R. (December 1987). "MIS: A Multiple-Level Logic Optimization System". IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems. 6 (6): 1062–1081. doi:10.1109/TCAD.1987.1270347. (MIS)
• De Geus, Aart J.; Cohen, William W. (1985). "A Rule-Based System for Optimizing Combinational Logic". IEEE Design & Test of Computers. 2 (4): 22–32. doi:10.1109/MDT.1985.294719. S2CID 46651690. (SOCRATES)