Metastability (electronics)

Metastability in electronics is the ability of a digital electronics system to persist for an unbounded time in an unstable equilibrium or metastable state.[1] In digital logic circuits, a digital signal is required to be within certain voltage or current limits to represent a '0' or '1' logic level for correct circuit operation; if the signal is within a forbidden intermediate range it may cause faulty behavior in logic gates the signal is applied to. In metastable states, the circuit may be unable to settle into a stable '0' or '1' logic level within the time required for proper circuit operation. As a result, the circuit can act in unpredictable ways, and may lead to a system failure, sometimes referred to as a "glitch".[2] Metastability is an instance of the Buridan's ass paradox.

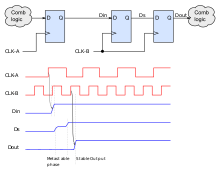
For other uses of the term, see Metastability.

An illustration of metastability in a synchronizer, where data crosses between clock domains. In the worst case, depending on timing, the metastable condition at Ds can propagate to Dout and through the following logic into more of the system, causing undefined and inconsistent behavior.

Metastable states are inherent features of asynchronous digital systems, and of systems with more than one independent clock domain. In self-timed asynchronous systems, arbiters are designed to allow the system to proceed only after the metastability has resolved, so the metastability is a normal condition, not an error condition.[3] In synchronous systems with asynchronous inputs, synchronizers are designed to make the probability of a synchronization failure acceptably small.[4] Metastable states are avoidable in fully synchronous systems when the input setup and hold time requirements on flip-flops are satisfied.

Example
The Set–Reset NOR latch example

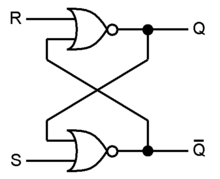
A simple example of metastability can be found in an SR NOR latch, when both Set and Reset inputs are true (R=1 and S=1) and then both transition to false (R=0 and S=0) at about the same time. Both outputs Q and Q are initially held at 0 by the simultaneous Set and Reset inputs. After both Set and Reset inputs change to false, the flip-flop will (eventually) end up in one of two stable states, one of Q and Q true and the other false. The final state will depend on which of R or S returns to zero first, chronologically, but if both transition at about the same time, the resulting metastability, with intermediate or oscillatory output levels, can take arbitrarily long to resolve to a stable state.

Arbiters
Main article: arbiter (electronics)

In electronics, an arbiter is a circuit designed to determine which of several signals arrive first. Arbiters are used in asynchronous circuits to order computational activities for shared resources to prevent concurrent incorrect operations. Arbiters are used on the inputs of fully synchronous systems, and also between clock domains, as synchronizers for input signals. Although they can minimize the occurrence of metastability to very low probabilities, all arbiters nevertheless have metastable states, which are unavoidable at the boundaries of regions of the input state space resulting in different outputs.[5]

Synchronous circuits
Synchronizers are used when transferring signals between clock domains. One simple synchronizer design involves simply delaying the input signal (data0) from a different clock domain using multiple edge sensitive flip-flops which are locally clocked (clock0)

Synchronous circuit design techniques make digital circuits that are resistant to the failure modes that can be caused by metastability. A clock domain is defined as a group of flip-flops with a common clock. Such architectures can form a circuit guaranteed free of metastability (below a certain maximum clock frequency, above which first metastability, then outright failure occur), assuming a low-skew common clock. However, even then, if the system has a dependence on any continuous inputs then these are likely to be vulnerable to metastable states.[6]

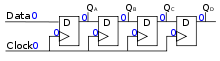
When synchronous design techniques are used, protection against metastable events causing systems failures need only be provided when transferring data between different clock domains or from an unclocked region into the synchronous system. This protection can often take the form of a series of delay flip-flops which delay the data stream long enough for metastability failures to occur at a negligible rate.

Failure modes

Although metastability is well understood and architectural techniques to control it are known, it persists as a failure mode in equipment.

Serious computer and digital hardware bugs caused by metastability have a fascinating social history. Many engineers have refused to believe that a bistable device can enter into a state that is neither true nor false and has a positive probability that it will remain indefinite for any given period of time, albeit with exponentially decreasing probability over time.[7][8][9][10][11] However, metastability is an inevitable result of any attempt to map a continuous domain to a discrete one. At the boundaries in the continuous domain between regions which map to different discrete outputs, points arbitrarily close together in the continuous domain map to different outputs, making a decision as to which output to select a difficult and potentially lengthy process.[12] If the inputs to an arbiter or flip-flop arrive almost simultaneously, the circuit most likely will traverse a point of metastability. Metastability remains poorly understood in some circles, and various engineers have proposed their own circuits said to solve or filter out the metastability; typically these circuits simply shift the occurrence of metastability from one place to another.[13] Chips using multiple clock sources are often tested with tester clocks that have fixed phase relationships, not the independent clocks drifting past each other that will be experienced during operation. This usually explicitly prevents the metastable failure mode that will occur in the field from being seen or reported. Proper testing for metastability often employs clocks of slightly different frequencies and ensuring correct circuit operation.

gollark: You mean a part list? Sure!
gollark: There's the 1660 Ti though.
gollark: The 1160 Ti never happened because Nvidia.
gollark: Well, that sounds... insanely expensive.
gollark: I hope we can agree that AMD *and* Nvidia have weird naming schemes sometimes.

See also

References
  1. Thomas J. Chaney and Charles E. Molnar (April 1973). "Anomalous Behavior of Synchronizer and Arbiter Circuits" (PDF). IEEE Transactions on Computers. C-22 (4): 421–422. doi:10.1109/T-C.1973.223730. ISSN 0018-9340.
  2. Chaney, Thomas J. "My Work on All Things Metastable OR Me and My Glitch" (PDF). Archived from the original (PDF) on 2015-12-08. Retrieved 2015-11-05.
  3. John Bainbridge (2002). Asynchronous system-on-chip interconnect. Springer. p. 18. ISBN 978-1-85233-598-4.
  4. Chaney, Thomas J. ""Reprint of Technical Memorandum No. 10, "The Glitch Phenomenon" (1966)"".Washington University St. Louis, MO
  5. Richard F. Tinder (2009). Asynchronous sequential machine design and analysis: a comprehensive development of the design and analysis of clock-independent state machines and systems. Morgan & Claypool Publishers. p. 165. ISBN 978-1-59829-689-1.
  6. Kleeman, L.; Cantoni, A. "Metastable Behavior in Digital Systems" December 1987". IEEE Design & Test of Computers. 4 (6): 4–19. doi:10.1109/MDT.1987.295189.
  7. Harris, Sarah; Harris, David (2015). Digital Design and Computer Architecture: ARM Edition. Morgan Kaufmann. pp. 151–153. ISBN 012800911X.
  8. Ginosar, Ran (2011). "Metastability and Synchronizers: A tutorial" (PDF). VLSI Systems Research Center. Electrical Engineering and Computer Science Dept., Technion—Israel Institute of Technology, Haifa., p. 4-6
  9. Xanthopoulos, Thucydides (2009). Clocking in Modern VLSI Systems. Springer Science and Business Media. p. 196. ISBN 1441902619., p. 196, 200, eq. 6-29
  10. "A Metastability Primer" (PDF). Application Note AN-219. Phillips Semiconductor. 1989. Retrieved 2017-01-20.
  11. Arora, Mohit (2011). The Art of Hardware Architecture: Design Methods and Techniques for Digital Circuits. Springer Science and Business Media. ISBN 1461403979., p. 4-5, eq. 1-1
  12. Leslie Lamport (February 2012) [December 1984]. "Buridan's Principle" (PDF). Retrieved 2010-07-09.
  13. Ran Ginosar. "Fourteen Ways to Fool Your Synchronizer" ASYNC 2003.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.