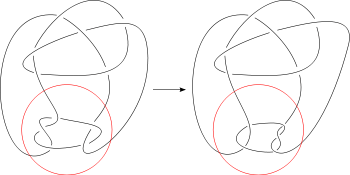
List of prime knots
In knot theory, prime knots are those knots that are indecomposable under the operation of knot sum. The prime knots with ten or fewer crossings are listed here for quick comparison of their properties and varied naming schemes.
Table of prime knots
Six or fewer crossings
| Name | Picture | Alexander- Briggs- Rolfsen |
Dowker- Thistlethwaite |
Dowker notation |
Conway notation |
|---|---|---|---|---|---|
| Unknot |  |
01 | 0a1 | — | — |
| Trefoil knot |  |
31 | 3a1 | 4 6 2 | [3] |
| Figure-eight knot |  |
41 | 4a1 | 4 6 8 2 | [22] |
| Cinquefoil knot |  |
51 | 5a2 | 6 8 10 2 4 | [5] |
| Three-twist knot |  |
52 | 5a1 | 4 8 10 2 6 | [32] |
| Stevedore knot |  |
61 | 6a3 | 4 8 12 10 2 6 | [42] |
| 62 knot |  |
62 | 6a2 | 4 8 10 12 2 6 | [312] |
| 63 knot |  |
63 | 6a1 | 4 8 10 2 12 6 | [2112] |
Seven crossings
| Picture | Alexander- Briggs- Rolfsen |
Dowker- Thistlethwaite |
Dowker notation | Conway notation |
|---|---|---|---|---|
 |
71 | 7a7 | 8 10 12 14 2 4 6 | [7] |
 |
72 | 7a4 | 4 10 14 12 2 8 6 | [52] |
 |
73 | 7a5 | 6 10 12 14 2 4 8 | [43] |
| 74 | 7a6 | 6 10 12 14 4 2 8 | [313] | |
| 75 | 7a3 | 4 10 12 14 2 8 6 | [322] | |
 |
76 | 7a2 | 4 8 12 2 14 6 10 | [2212] |
 |
77 | 7a1 | 4 8 10 12 2 14 6 | [21112] |
Eight crossings
| Picture | Alexander- Briggs- Rolfsen |
Dowker- Thistlethwaite |
Dowker notation | Conway notation |
|---|---|---|---|---|
 |
81 | 8a11 | 4 10 16 14 12 2 8 6 | [62] |
 |
82 | 8a8 | 4 10 12 14 16 2 6 8 | [512] |
 |
83 | 8a18 | 6 12 10 16 14 4 2 8 | [44] |
 |
84 | 8a17 | 6 10 12 16 14 4 2 8 | [413] |
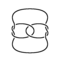 |
85 | 8a13 | 6 8 12 2 14 16 4 10 | [3,3,2] |
 |
86 | 8a10 | 4 10 14 16 12 2 8 6 | [332] |
| 87 | 8a6 | 4 10 12 14 2 16 6 8 | [4112] | |
| 88 | 8a4 | 4 8 12 2 16 14 6 10 | [2312] | |
| 89 | 8a16 | 6 10 12 14 16 4 2 8 | [3113] | |
| 810 | 8a3 | 4 8 12 2 14 16 6 10 | [3,21,2] | |
| 811 | 8a9 | 4 10 12 14 16 2 8 6 | [3212] | |
 |
812 | 8a5 | 4 8 14 10 2 16 6 12 | [2222] |
| 813 | 8a7 | 4 10 12 14 2 16 8 6 | [31112] | |
| 814 | 8a1 | 4 8 10 14 2 16 6 12 | [22112] | |
| 815 | 8a2 | 4 8 12 2 14 6 16 10 | [21,21,2] | |
 |
816 | 8a15 | 6 8 14 12 4 16 2 10 | [.2.20] |
 |
817 | 8a14 | 6 8 12 14 4 16 2 10 | [.2.2] |
 |
818 | 8a12 | 6 8 10 12 14 16 2 4 | [8*] |
 |
819 | 8n3 | 4 8 -12 2 -14 -16 -6 -10 | [3,3,2-] |
 |
820 | 8n1 | 4 8 -12 2 -14 -6 -16 -10 | [3,21,2-] |
 |
821 | 8n2 | 4 8 -12 2 14 -6 16 10 | [21,21,2-] |
Nine crossings
| Picture | Alexander- Briggs- Rolfsen |
Dowker- Thistlethwaite |
Dowker notation | Conway notation |
|---|---|---|---|---|
 |
91 | 9a41 | 10 12 14 16 18 2 4 6 8 | [9] |
| 92 | 9a27 | 4 12 18 16 14 2 10 8 6 | [72] | |
| 93 | 9a38 | 8 12 14 16 18 2 4 6 10 | [63] | |
| 94 | 9a35 | 6 12 14 18 16 2 4 10 8 | [54] | |
| 95 | 9a36 | 6 12 14 18 16 4 2 10 8 | [513] | |
| 96 | 9a23 | 4 12 14 16 18 2 10 6 8 | [522] | |
| 97 | 9a26 | 4 12 16 18 14 2 10 8 6 | [342] | |
| 98 | 9a8 | 4 8 14 2 18 16 6 12 10 | [2412] | |
| 99 | 9a33 | 6 12 14 16 18 2 4 10 8 | [423] | |
| 910 | 9a39 | 8 12 14 16 18 2 6 4 10 | [333] | |
| 911 | 9a20 | 4 10 14 16 12 2 18 6 8 | [4122] | |
| 912 | 9a22 | 4 10 16 14 2 18 8 6 12 | [4212] | |
| 913 | 9a34 | 6 12 14 16 18 4 2 10 8 | [3213] | |
| 914 | 9a17 | 4 10 12 16 14 2 18 8 6 | [41112] | |
| 915 | 9a10 | 4 8 14 10 2 18 16 6 12 | [2322] | |
| 916 | 9a25 | 4 12 16 18 14 2 8 10 6 | [3,3,2+] | |
| 917 | 9a14 | 4 10 12 14 16 2 6 18 8 | [21312] | |
| 918 | 9a24 | 4 12 14 16 18 2 10 8 6 | [3222] | |
| 919 | 9a3 | 4 8 10 14 2 18 16 6 12 | [23112] | |
| 920 | 9a19 | 4 10 14 16 2 18 8 6 12 | [31212] | |
| 921 | 9a21 | 4 10 14 16 12 2 18 8 6 | [31122] | |
| 922 | 9a2 | 4 8 10 14 2 16 18 6 12 | [211,3,2] | |
| 923 | 9a16 | 4 10 12 16 2 8 18 6 14 | [22122] | |
| 924 | 9a7 | 4 8 14 2 16 18 6 12 10 | [3,21,2+] | |
| 925 | 9a4 | 4 8 12 2 16 6 18 10 14 | [22,21,2] | |
| 926 | 9a15 | 4 10 12 14 16 2 18 8 6 | [311112] | |
| 927 | 9a12 | 4 10 12 14 2 18 16 6 8 | [212112] | |
| 928 | 9a5 | 4 8 12 2 16 14 6 18 10 | [21,21,2+] | |
| 929 | 9a31 | 6 10 14 18 4 16 8 2 12 | [.2.20.2] | |
| 930 | 9a1 | 4 8 10 14 2 16 6 18 12 | [211,21,2] | |
| 931 | 9a13 | 4 10 12 14 2 18 16 8 6 | [2111112] | |
| 932 | 9a6 | 4 8 12 14 2 16 18 10 6 | [.21.20] | |
| 933 | 9a11 | 4 8 14 12 2 16 18 10 6 | [.21.2] | |
| 934 | 9a28 | 6 8 10 16 14 18 4 2 12 | [8*20] | |
 |
935 | 9a40 | 8 12 16 14 18 4 2 6 10 | [3,3,3] |
| 936 | 9a9 | 4 8 14 10 2 16 18 6 12 | [22,3,2] | |
| 937 | 9a18 | 4 10 14 12 16 2 6 18 8 | [3,21,21] | |
| 938 | 9a30 | 6 10 14 18 4 16 2 8 12 | [.2.2.2] | |
| 939 | 9a32 | 6 10 14 18 16 2 8 4 12 | [2:2:20] | |
 |
940 | 9a27 | 6 16 14 12 4 2 18 10 8 | [9*] |
 |
941 | 9a29 | 6 10 14 12 16 2 18 4 8 | [20:20:20] |
| 942 | 9n4 | 4 8 10 −14 2 −16 −18 −6 −12 | [22,3,2−] | |
| 943 | 9n3 | 4 8 10 14 2 −16 6 −18 −12 | [211,3,2−] | |
| 944 | 9n1 | 4 8 10 −14 2 −16 −6 −18 −12 | [22,21,2−] | |
| 945 | 9n2 | 4 8 10 −14 2 16 −6 18 12 | [211,21,2−] | |
| 946 | 9n5 | 4 10 −14 −12 −16 2 −6 −18 −8 | [3,3,21−] | |
 |
947 | 9n7 | 6 8 10 16 14 −18 4 2 −12 | [8*-20] |
| 948 | 9n6 | 4 10 −14 −12 16 2 −6 18 8 | [21,21,21−] | |
| 949 | 9n8 | 6 -10 −14 12 −16 −2 18 −4 −8 | [−20:−20:−20] |
Ten crossings
| Picture | Alexander- Briggs- Rolfsen |
Dowker- Thistlethwaite |
Dowker notation | Conway notation |
|---|---|---|---|---|
| 101 | 10a75 | 4 12 20 18 16 14 2 10 8 6 | [82] | |
| 102 | 10a59 | 4 12 14 16 18 20 2 6 8 10 | [712] | |
| 103 | 10a117 | 6 14 12 20 18 16 4 2 10 8 | [64] | |
| 104 | 10a113 | 6 12 14 20 18 16 4 2 10 8 | [613] | |
| 105 | 10a56 | 4 12 14 16 18 2 20 6 8 10 | [6112] | |
| 106 | 10a70 | 4 12 16 18 20 14 2 10 6 8 | [532] | |
| 107 | 10a65 | 4 12 14 18 16 20 2 10 8 6 | [5212] | |
| 108 | 10a114 | 6 14 12 16 18 20 4 2 8 10 | [514] | |
| 109 | 10a110 | 6 12 14 16 18 20 4 2 8 10 | [5113] | |
| 1010 | 10a64 | 4 12 14 18 16 2 20 10 8 6 | [51112] | |
| 1011 | 10a116 | 6 14 12 18 20 16 4 2 10 8 | [433] | |
| 1012 | 10a43 | 4 10 14 16 2 20 18 6 8 12 | [4312] | |
| 1013 | 10a54 | 4 10 18 16 12 2 20 8 6 14 | [4222] | |
| 1014 | 10a33 | 4 10 12 16 18 2 20 6 8 14 | [42112] | |
| 1015 | 10a68 | 4 12 16 18 14 2 10 20 6 8 | [4132] | |
| 1016 | 10a115 | 6 14 12 16 18 20 4 2 10 8 | [4123] | |
| 1017 | 10a107 | 6 12 14 16 18 2 4 20 8 10 | [4114] | |
| 1018 | 10a63 | 4 12 14 18 16 2 10 20 8 6 | [41122] | |
| 1019 | 10a108 | 6 12 14 16 18 2 4 20 10 8 | [41113] | |
| 1020 | 10a74 | 4 12 18 20 16 14 2 10 8 6 | [352] | |
| 1021 | 10a60 | 4 12 14 16 18 20 2 6 10 8 | [3412] | |
| 1022 | 10a112 | 6 12 14 18 20 16 4 2 10 8 | [3313] | |
| 1023 | 10a57 | 4 12 14 16 18 2 20 6 10 8 | [33112] | |
| 1024 | 10a71 | 4 12 16 18 20 14 2 10 8 6 | [3232] | |
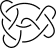 |
1025 | 10a61 | 4 12 14 16 18 20 2 10 8 6 | [32212] |
| 1026 | 10a111 | 6 12 14 16 18 20 4 2 10 8 | [32113] | |
| 1027 | 10a58 | 4 12 14 16 18 2 20 10 8 6 | [321112] | |
| 1028 | 10a44 | 4 10 14 16 2 20 18 8 6 12 | [31312] | |
| 1029 | 10a53 | 4 10 16 18 12 2 20 8 6 14 | [31222] | |
| 1030 | 10a34 | 4 10 12 16 18 2 20 8 6 14 | [312112] | |
| 1031 | 10a69 | 4 12 16 18 14 2 10 20 8 6 | [31132] | |
| 1032 | 10a55 | 4 12 14 16 18 2 10 20 8 6 | [311122] | |
| 1033 | 10a109 | 6 12 14 16 18 4 2 20 10 8 | [311113] | |
| 1034 | 10a19 | 4 8 14 2 20 18 16 6 12 10 | [2512] | |
| 1035 | 10a23 | 4 8 16 10 2 20 18 6 14 12 | [2422] | |
| 1036 | 10a5 | 4 8 10 16 2 20 18 6 14 12 | [24112] | |
| 1037 | 10a49 | 4 10 16 12 2 8 20 18 6 14 | [2332] | |
| 1038 | 10a29 | 4 10 12 16 2 8 20 18 6 14 | [23122] | |
| 1039 | 10a26 | 4 10 12 14 18 2 6 20 8 16 | [22312] | |
| 1040 | 10a30 | 4 10 12 16 2 20 6 18 8 14 | [222112] | |
| 1041 | 10a35 | 4 10 12 16 20 2 8 18 6 14 | [221212] | |
| 1042 | 10a31 | 4 10 12 16 2 20 8 18 6 14 | [2211112] | |
| 1043 | 10a52 | 4 10 16 14 2 20 8 18 6 12 | [212212] | |
| 1044 | 10a32 | 4 10 12 16 14 2 20 18 8 6 | [2121112] | |
| 1045 | 10a25 | 4 10 12 14 16 2 20 18 8 6 | [21111112] | |
| 1046 | 10a81 | 6 8 14 2 16 18 20 4 10 12 | [5,3,2] | |
| 1047 | 10a15 | 4 8 14 2 16 18 20 6 10 12 | [5,21,2] | |
| 1048 | 10a79 | 6 8 14 2 16 18 4 20 10 12 | [41,3,2] | |
| 1049 | 10a13 | 4 8 14 2 16 18 6 20 10 12 | [41,21,2] | |
| 1050 | 10a82 | 6 8 14 2 16 18 20 4 12 10 | [32,3,2] | |
| 1051 | 10a16 | 4 8 14 2 16 18 20 6 12 10 | [32,21,2] | |
| 1052 | 10a80 | 6 8 14 2 16 18 4 20 12 10 | [311,3,2] | |
| 1053 | 10a14 | 4 8 14 2 16 18 6 20 12 10 | [311,21,2] | |
| 1054 | 10a48 | 4 10 16 12 2 8 18 20 6 14 | [23,3,2] | |
| 1055 | 10a9 | 4 8 12 2 16 6 20 18 10 14 | [23,21,2] | |
| 1056 | 10a28 | 4 10 12 16 2 8 18 20 6 14 | [221,3,2] | |
| 1057 | 10a6 | 4 8 12 2 14 18 6 20 10 16 | [221,21,2] | |
| 1058 | 10a20 | 4 8 14 10 2 18 6 20 12 16 | [22,22,2] | |
 |
1059 | 10a2 | 4 8 10 14 2 18 6 20 12 16 | [22,211,2] |
 |
1060 | 10a1 | 4 8 10 14 2 16 18 6 20 12 | [211,211,2] |
| 1061 | 10a123 | 8 10 16 14 2 18 20 6 4 12 | [4,3,3] | |
| 1062 | 10a41 | 4 10 14 16 2 18 20 6 8 12 | [4,3,21] | |
| 1063 | 10a51 | 4 10 16 14 2 18 8 6 20 12 | [4,21,21] | |
| 1064 | 10a122 | 8 10 14 16 2 18 20 6 4 12 | [31,3,3] | |
| 1065 | 10a42 | 4 10 14 16 2 18 20 8 6 12 | [31,3,21] | |
| 1066 | 10a40 | 4 10 14 16 2 18 8 6 20 12 | [31,21,21] | |
| 1067 | 10a37 | 4 10 14 12 18 2 6 20 8 16 | [22,3,21] | |
| 1068 | 10a67 | 4 12 16 14 18 2 20 6 10 8 | [211,3,3] | |
| 1069 | 10a38 | 4 10 14 12 18 2 16 6 20 8 | [211,21,21] | |
| 1070 | 10a22 | 4 8 16 10 2 18 20 6 14 12 | [22,3,2+] | |
| 1071 | 10a10 | 4 8 12 2 18 14 6 20 10 16 | [22,21,2+] | |
| 1072 | 10a4 | 4 8 10 16 2 18 20 6 14 12 | [211,3,2+] | |
| 1073 | 10a3 | 4 8 10 14 2 18 16 6 20 12 | [211,21,2+] | |
| 1074 | 10a62 | 4 12 14 16 20 18 2 8 6 10 | [3,3,21+] | |
| 1075 | 10a27 | 4 10 12 14 18 2 16 6 20 8 | [21,21,21+] | |
| 1076 | 10a73 | 4 12 18 20 14 16 2 10 8 6 | [3,3,2++] | |
| 1077 | 10a18 | 4 8 14 2 18 20 16 6 12 10 | [3,21,2++] | |
| 1078 | 10a17 | 4 8 14 2 18 16 6 12 20 10 | [21,21,2++] | |
| 1079 | 10a78 | 6 8 12 2 16 4 18 20 10 14 | [(3,2)(3,2)] | |
| 1080 | 10a8 | 4 8 12 2 16 6 18 20 10 14 | [(3,2)(21,2)] | |
| 1081 | 10a7 | 4 8 12 2 16 6 18 10 20 14 | [(21,2)(21,2)] | |
| 1082 | 10a83 | 6 8 14 16 4 18 20 2 10 12 | [.4.2] | |
| 1083 | 10a84 | 6 8 16 14 4 18 20 2 12 10 | [.31.20] | |
| 1084 | 10a50 | 4 10 16 14 2 8 18 20 12 6 | [.22.2] | |
| 1085 | 10a86 | 6 8 16 14 4 18 20 2 10 12 | [.4.20] | |
| 1086 | 10a87 | 6 8 14 16 4 18 20 2 12 10 | [.31.2] | |
| 1087 | 10a39 | 4 10 14 16 2 8 18 20 12 6 | [.22.20] | |
| 1088 | 10a11 | 4 8 12 14 2 16 20 18 10 6 | [.21.21] | |
| 1089 | 10a21 | 4 8 14 12 2 16 20 18 10 6 | [.21.210] | |
| 1090 | 10a92 | 6 10 14 2 16 20 18 8 4 12 | [.3.2.2] | |
| 1091 | 10a106 | 6 10 20 14 16 18 4 8 2 12 | [.3.2.20] | |
| 1092 | 10a46 | 4 10 14 18 2 16 8 20 12 6 | [.21.2.20] | |
| 1093 | 10a101 | 6 10 16 20 14 4 18 2 12 8 | [.3.20.2] | |
| 1094 | 10a91 | 6 10 14 2 16 18 20 8 4 12 | [.30.2.2] | |
| 1095 | 10a47 | 4 10 14 18 2 16 20 8 12 6 | [.210.2.2] | |
| 1096 | 10a24 | 4 8 18 12 2 16 20 6 10 14 | [.2.21.2] | |
| 1097 | 10a12 | 4 8 12 18 2 16 20 6 10 14 | [.2.210.2] | |
| 1098 | 10a96 | 6 10 14 18 2 16 20 4 8 12 | [.2.2.2.20] | |
| 1099 | 10a103 | 6 10 18 14 2 16 20 8 4 12 | [.2.2.20.20] | |
| 10100 | 10a104 | 6 10 18 14 16 4 20 8 2 12 | [3:2:2] | |
| 10101 | 10a45 | 4 10 14 18 2 16 6 20 8 12 | [21:2:2] | |
| 10102 | 10a97 | 6 10 14 18 16 4 20 2 8 12 | [3:2:20] | |
| 10103 | 10a105 | 6 10 18 16 14 4 20 8 2 12 | [30:2:2] | |
| 10104 | 10a118 | 6 16 12 14 18 4 20 2 8 10 | [3:20:20] | |
| 10105 | 10a72 | 4 12 16 20 18 2 8 6 10 14 | [21:20:20] | |
| 10106 | 10a95 | 6 10 14 16 18 4 20 2 8 12 | [30:2:20] | |
| 10107 | 10a66 | 4 12 16 14 18 2 8 20 10 6 | [210:2:20] | |
| 10108 | 10a119 | 6 16 12 14 18 4 20 2 10 8 | [30:20:20] | |
| 10109 | 10a93 | 6 10 14 16 2 18 4 20 8 12 | [2.2.2.2] | |
| 10110 | 10a100 | 6 10 16 20 14 2 18 4 8 12 | [2.2.2.20] | |
| 10111 | 10a98 | 6 10 16 14 2 18 8 20 4 12 | [2.2.20.2] | |
| 10112 | 10a76 | 6 8 10 14 16 18 20 2 4 12 | [8*3] | |
| 10113 | 10a36 | 4 10 14 12 2 16 18 20 8 6 | [8*21] | |
| 10114 | 10a77 | 6 8 10 14 16 20 18 2 4 12 | [8*30] | |
| 10115 | 10a94 | 6 10 14 16 4 18 2 20 12 8 | [8*20.20] | |
 |
10116 | 10a120 | 6 16 18 14 2 4 20 8 10 12 | [8*2:2] |
| 10117 | 10a99 | 6 10 16 14 18 4 20 2 12 8 | [8*2:20] | |
| 10118 | 10a88 | 6 8 18 14 16 4 20 2 10 12 | [8*2:.2] | |
| 10119 | 10a85 | 6 8 14 18 16 4 20 10 2 12 | [8*2:.20] | |
 |
10120 | 10a102 | 6 10 18 12 4 16 20 8 2 14 | [8*20::20] |
| 10121 | 10a90 | 6 10 12 20 18 16 8 2 4 14 | [9*20] | |
| 10122 | 10a89 | 6 10 12 14 18 16 20 2 4 8 | [9*.20] | |
.svg.png) |
10123 | 10a121 | 8 10 12 14 16 18 20 2 4 6 | [10*] |
| 10124 | 10n21 | 4 8 -14 2 -16 -18 -20 -6 -10 -12 | [5,3,2-] | |
| 10125 | 10n15 | 4 8 14 2 -16 -18 6 -20 -10 -12 | [5,21,2-] | |
| 10126 | 10n17 | 4 8 -14 2 -16 -18 -6 -20 -10 -12 | [41,3,2-] | |
| 10127 | 10n16 | 4 8 -14 2 16 18 -6 20 10 12 | [41,21,2-] | |
| 10128 | 10n22 | 4 8 -14 2 -16 -18 -20 -6 -12 -10 | [32,3,2-] | |
| 10129 | 10n18 | 4 8 14 2 -16 -18 6 -20 -12 -10 | [32,21,-2] | |
| 10130 | 10n20 | 4 8 -14 2 -16 -18 -6 -20 -12 -10 | [311,3,2-] | |
| 10131 | 10n19 | 4 8 -14 2 16 18 -6 20 12 10 | [311,21,2-] | |
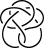 |
10132 | 10n13 | 4 8 -12 2 -16 -6 -20 -18 -10 -14 | [23,3,2-] |
| 10133 | 10n4 | 4 8 12 2 -14 -18 6 -20 -10 -16 | [23,21,2-] | |
| 10134 | 10n6 | 4 8 -12 2 -14 -18 -6 -20 -10 -16 | [221,3,2-] | |
| 10135 | 10n5 | 4 8 -12 2 14 18 -6 20 10 16 | [221,21,2-] | |
| 10136 | 10n3 | 4 8 10 -14 2 -18 -6 -20 -12 -16 | [22,22,2-] | |
| 10137 | 10n2 | 4 8 10 -14 2 -16 -18 -6 -20 -12 | [22,211,2-] | |
| 10138 | 10n1 | 4 8 10 -14 2 16 18 -6 20 12 | [211,211,2-] | |
| 10139 | 10n27 | 4 10 -14 -16 2 -18 -20 -6 -8 -12 | [4,3,3-] | |
| 10140 | 10n29 | 4 10 -14 -16 2 18 20 -8 -6 12 | [4,3,21-] | |
| 10141 | 10n25 | 4 10 -14 -16 2 18 -8 -6 20 12 | [4,21,21-] | |
| 10142 | 10n30 | 4 10 -14 -16 2 -18 -20 -8 -6 -12 | [31,3,3-] | |
| 10143 | 10n26 | 4 10 -14 -16 2 -18 -8 -6 -20 -12 | [31,3,21-] | |
| 10144 | 10n28 | 4 10 14 16 2 -18 -20 8 6 -12 | [31,21,21-] | |
| 10145 | 10n14 | 4 8 -12 -18 2 -16 -20 -6 -10 -14 | [22,3,3-] | |
| 10146 | 10n23 | 4 8 -18 -12 2 -16 -20 -6 -10 -14 | [22,21,21-] | |
| 10147 | 10n24 | 4 10 -14 12 2 16 18 -20 8 -6 | [211,3,21-] | |
| 10148 | 10n12 | 4 8 -12 2 -16 -6 -18 -20 -10 -14 | [(3,2)(3,2-)] | |
| 10149 | 10n11 | 4 8 -12 2 16 -6 18 20 10 14 | [(3,2)(21,2-)] | |
| 10150 | 10n9 | 4 8 -12 2 -16 -6 -18 -10 -20 -14 | [(21,2)(3,2-)] | |
| 10151 | 10n8 | 4 8 -12 2 16 -6 18 10 20 14 | [(21,2)(21,2-)] | |
| 10152 | 10n36 | 6 8 12 2 -16 4 -18 -20 -10 -14 | [(3,2)-(3,2)] | |
| 10153 | 10n10 | 4 8 12 2 -16 6 -18 -20 -10 -14 | [(3,2)-(21,2)] | |
| 10154 | 10n7 | 4 8 12 2 -16 6 -18 -10 -20 -14 | [(21,2)-(21,2)] | |
| 10155 | 10n39 | 6 10 14 16 18 4 -20 2 8 -12 | [-3:2:2] | |
| 10156 | 10n32 | 4 12 16 -14 18 2 -8 20 10 6 | [-3:2:20] | |
| 10157 | 10n42 | 6 -10 -18 14 -2 -16 20 8 -4 12 | [-3:20:20] | |
| 10158 | 10n41 | 6 -10 -16 14 -2 -18 8 20 -4 -12 | [-30:2:2] | |
| 10159 | 10n34 | 6 8 10 14 16 -18 -20 2 4 -12 | [-30:2:20] | |
| 10160 | 10n33 | 4 12 -16 -14 -18 2 -8 -20 -10 -6 | [-30:20:20] | |
| 10161[lower-alpha 1] | 10n31 | 4 12 -16 14 -18 2 8 -20 -10 -6 | [3:-20:-20] | |
| 10162[lower-alpha 2] | 10n40 | 6 10 14 18 16 4 -20 2 8 -12 | [-30:-20:-20] | |
| 10163[lower-alpha 3] | 10n35 | 6 8 10 14 16 -20 -18 2 4 -12 | [8*-30] | |
| 10164[lower-alpha 4] | 10n38 | 6 -10 -12 14 -18 -16 20 -2 -4 -8 | [8*2:-20] | |
| 10165[lower-alpha 5] | 10n37 | 6 8 14 18 16 4 -20 10 2 -12 | [8*2:.-20] |
Table of prime links
Seven or fewer crossings
| Name | Picture | Alexander- Briggs- Rolfsen |
Dowker-
Thistlethwaite |
Dowker notation | Conway notation |
|---|---|---|---|---|---|
| Unlink | 02 1 |
— | — | — | |
| Hopf link | 22 1 |
L2a1 | — | [2] | |
| Solomon's knot |
 |
42 1 |
L4a1 | — | [4] |
| Whitehead link |
 |
52 1 |
L5a1 | — | [212] |
| L6a1 | 62 3 |
L6a1 | — | — | |
| L6a2 | 62 2 |
L6a2 | — | — | |
| L6a3 | 62 1 |
L6a3 | — | — | |
| Borromean rings |
 |
63 2 |
L6a4 | — | [.1] |
| L6a5 | 63 1 |
L6a5 | — | — | |
| L6n1 |  |
63 3 |
L6n1 | — | — |
| L7a1 | 72 6 |
L7a1 | — | — | |
| L7a2 | 72 5 |
L7a2 | — | — | |
| L7a3 | 72 4 |
L7a3 | — | — | |
| L7a4 | 72 3 |
L7a4 | — | — | |
| L7a5 | 72 2 |
L7a5 | — | — | |
| L7a6 | 72 1 |
L7a6 | — | — | |
| L7a7 | 73 1 |
L7a7 | — | — | |
| L7n1 | 72 7 |
L7n1 | — | — | |
| L7n2 | 72 8 |
L7n2 | (6,-8|-10,12,-14,2,-4) | — |
Higher
.png)
(36,3)-torus link
| Picture | Alexander- Briggs- Rolfsen |
Dowker- Thistlethwaite |
Dowker notation | Conway notation |
|---|---|---|---|---|
| 82 1 |
L8a14 | — | — | |
 |
— | L10a140 | — | [.3:30] |
gollark: ÆæÆÆÆÆÆÆÆÆÆÆÆÆææÆÆÆÆÆÆÆÆÆÆÆÆÆæææÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆæææææÆÆÆÆÆÆÆÆÆÆÆÆææææææÆææææææÆÆÆÆÆæææææÆÆææÆÆæææææææææÆÆÆæææÆÆÆæææÆÆÆæÆÆÆÆæ
gollark: ÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆA
gollark: ÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆ
gollark: Unless you explicitly obfuscate it, you *basically* get the original program out, without comments and such.
gollark: I totally\* know about that, I once ran a C# program through a decompiler.
Notes
- Originally listed as both 10161 and 10162 in the Rolfsen table. The error was discovered by Kenneth Perko (see Perko pair).
- Listed as 10163 in the Rolfsen table.
- Listed as 10164 in the Rolfsen table.
- Listed as 10165 in the Rolfsen table.
- Listed as 10166 in the Rolfsen table.
External links
- "The Rolfsen Knot Table", The Knot Atlas.
- "KnotInfo", Indiana.edu.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.