Hyperbolic link

In mathematics, a hyperbolic link is a link in the 3-sphere with complement that has a complete Riemannian metric of constant negative curvature, i.e. has a hyperbolic geometry. A hyperbolic knot is a hyperbolic link with one component.

41 knot

As a consequence of the work of William Thurston, it is known that every knot is precisely one of the following: hyperbolic, a torus knot, or a satellite knot. As a consequence, hyperbolic knots can be considered plentiful. A similar heuristic applies to hyperbolic links.

As a consequence of Thurston's hyperbolic Dehn surgery theorem, performing Dehn surgeries on a hyperbolic link enables one to obtain many more hyperbolic 3-manifolds.

Examples
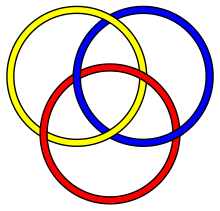
Borromean rings are a hyperbolic link.
gollark: I mean, if you want something based on prime numbers, then I guess you can make that work manually.
gollark: Kind of.
gollark: ROT1 technically fits.
gollark: Deflate then. WhatEVER.
gollark: Compare their speed.

See also

Further reading
  • Colin Adams (1994, 2004) The Knot Book, American Mathematical Society, ISBN 0-8050-7380-9.
  • William Menasco (1984) "Closed incompressible surfaces in alternating knot and link complements", Topology 23(1):37–44.
  • William Thurston (1978-1981) The geometry and topology of three-manifolds, Princeton lecture notes.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.