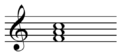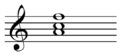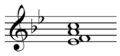Inversions higher than third
Inversions higher than the third require extended chords; the fourth inversion requires a ninth chord, the fifth an eleventh chord, etc.
If you're working with extended chords, there are more than two possible inversions. For example, the third inversion of a seventh chord puts the seventh in the bass; the fourth inversion of a ninth chord puts the ninth in the bass.[2]
(higher inversions)
6
4
2-I.[lower-alpha 1]
5
4
2-I.

4
3
2-I6.
Fourth inversion
The fourth inversion of a ninth chord is the voicing in which the ninth of the chord is the bass note and the root a minor seventh above it. In the fourth inversion of a G-dominant ninth, the bass is A — the ninth of the chord — with the third, fifth, seventh, and root stacked above it, forming the intervals of a second, a fourth, a sixth, and a seventh above the inverted bass of A, respectively.
The chord of the ninth, having four intervals like the flat seventh, of course admits of four inversions in both major and minor... The...fourth inversion, ["marked"]: 642...is seldom used.
— John Smith (1853)[3]
If...the Ninth is in the bass: 4th inversion of a Ninth-chord.[4]
The ninth chord and its inversions exist today, or at least they can exist. The pupil will easily find examples in the literature [such as Schoenberg's Verklärte Nacht and Strauss's opera Salome]. It is not necessary to set up special laws for its treatment. If one wants to be careful, one will be able to use the laws that pertain to the seventh chords: that is, dissonances resolve by step downward, the root leaps a fourth upward.
Fifth inversion
The fifth inversion of an eleventh chord is the voicing in which the eleventh of the chord is the bass note and the root a perfect fourth above it. In the fifth inversion of a G-dominant eleventh with eleventh, the bass is C — the eleventh of the chord — with the root, third, fifth, seventh, and ninth stacked above it, forming the intervals of a second, a fourth, a fifth, a sixth, and a seventh above the inverted bass of C, respectively.
Sixth inversion
The sixth inversion of a thirteenth chord is the highest possible diatonic inversion, since the diatonic scale has seven notes. (The "seventh" inversion of the dominant thirteenth chord is root position.) Higher inversions would require chromaticism and either nonscale tones or scales with more than seven tones.
Arrangement of notes above the bass
Any voicing above the bass is allowed. For example, a fourth inversion must have the ninth chord factor in the bass, but it may have any arrangement of the root, third, fifth, and seventh above that, including doubled notes, compound intervals, and omission of the fifth (A-G-B-D-F, A-B-D-F-G-B′, A-G-D-F, etc.)
Inversions are not restricted to the same number of tones as the original chord, nor to any fixed order of tones except with regard to the interval between the root, or its octave, and the bass note, hence, great variety results.[1]
See also
Notes
- The fundamental position of a ninth chord is specified by 9
, the second inversion is 6
5
4
3, the third is 6
4
3
2, and the, "fourth inversion of a chord of the ninth," is 7
6
4
2.[1]
References
- Hubbard, William Lines (1908). The American History and Encyclopedia of Music: Musical Dictionary, p.103. Irving Squire: London. [ISBN unspecified]. Also at the HathiTrust Digital Library
- Miller, Michael (2002). The Complete Idiot's Guide to Music Theory, p.115. Penguin. ISBN 9780028643779.
- Smith, John (1853). A Treatise on the Theory and Practice of Music, p.27-8. J. McGlashan. [ISBN unspecified].
- Ziehn, Bernhard (1907). Manual of Harmony: Theoretical and Practical, Volume 1, p.4. Wm. A Kaun Music Company. [ISBN unspecified].
- Schoenberg, Arnold (1910). Theory of Harmony, p.346-7. University of California Press. First published in German as Harmonielehre in 1910. ISBN 9780520049444. Roman numeral analysis and arrows not included in the original.