Hawaiian scale

Hawaiian scale is an expression of the height of a wind wave affecting water. It is the expression conventionally used by surfers in Hawaii and is also used in Australia and parts of South Africa.

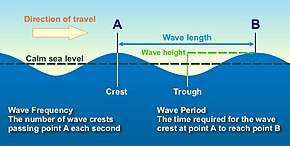
Figure showing the scientific standard of measuring significant wave height (from trough to crest). The Hawaiian scale would instead measure from calm sea level to crest, reporting half the height.

The expression, always given in feet, is a scaled figure corresponding to roughly half the actual measured or estimated height of a wave's face. Thus, a "3-foot" wave is roughly six feet high (in actuality an Hm0 of ~1.8 m), i.e., head-high to a 6-foot (~180 cm) person; a "2-foot" wave is roughly four feet high (Hm0 of ~1.2 m), i.e., chest-high to such a person; and a "6- to 8-foot" wave would be 2 to approaching 3 times head-high to such a person (Hm0 of ~3.5 to 5 m). As wave height increases, however, so does the difficulty of judging that height, and as wave height approaches 20 feet (Hm0 of 6 or 12 m, respectively), the range of absolute wave heights corresponding to a given scaled expression tends to widen.

The origin of the scale is obscure. Commentator Neal Miyake has proposed the following candidates:[1]

  • Hawaiian lifeguards' announcement of smaller wave sizes in an effort to minimize casual tourists' interest in a surf break (albeit at the risk of attracting novice surfers aware of their own limitations who might be deterred by an announcement of a larger wave size)
  • A possible local practice of taking measurements "from the back" of the wave, i.e., from mean sea level (in technical terms, of measuring not the "peak-to-peak amplitude" of the wave or the height of the wave's face, the latter of which is increased by the wave's drawing water from in front of it as it breaks, but rather the wave's "semi-amplitude" or "peak amplitude"), or from wave buoy readings
  • Modesty or false modesty in early surfers' reports of their own accomplishments

In Australia, which otherwise uses the metric system, surfers and surfer-oriented media such as Australia's Surfing Life and Tracks magazines still measure and describe waves in terms of feet. Some journalists and media outlets that provide information to surfers but are not staffed by insiders to the sport express wave size in metric units using direct conversion from a literal interpretation of the scale's output,[2] e.g., labeling as "1-metre" a wave that insiders would describe as "3-foot" or slightly larger. Such an attempt, however, is unsatisfactory both to surfers who do not use the converted units and to non-surfers and novices who do not realize that the trough-to-crest wave height is twice the figure quoted (in actuality, a Hm0 wave height of ~2 m from trough to crest).

Alternatives to the Hawaiian scale

Miyake reports[3] that the Surf News Network[4] expresses wave heights as "2/3 the height of the wave from crest to trough." This heuristic finds mathematical support as a compromise between two methods of expressing the combined effects of a wave's average upward and average downward deviations from mean sea level, namely a) the sum of the absolute value of a sine wave's average (mean) deviation during its upward half-cycle and the absolute value of that mean deviation during its downward half-cycle (|0.637| + |-0.637| ≈ 1.273)[5] and b) the sum of the root mean square (RMS) amplitude of each of those half-cycles, i.e., twice the RMS amplitude of either half-cycle (2[0.707] ≈ 1.4014), each of which expressions is within between 0.06 and 0.07, or within between 4.5% and 5.25%, of the value 1.3 yielded by the heuristic for that sine wave when ​2⁄3 is multiplied by the sine wave's crest-to-trough (peak-to-peak) amplitude of 2.

gollark: Fascinating.
gollark: I see you cannot rigorously justify your dislike of ABR in any way whatsoever.
gollark: e
gollark: π
gollark: sqrt(2)

See also

References
  1. Neal Miyake, "Hawaiian Scale: Measuring Wave Heights in Hawaii," Around Town: Hawaii, May 2003, available at https://web.archive.org/web/20051014143651/http://www.hawaii.rr.com/leisure/reviews/neal_miyake/2003-05_hsmwhihawaii.htm (archived from http://www.hawaii.rr.com:80/leisure/reviews/neal_miyake/2003-05_hsmwhihawaii.htm [link dead as of May 7, 2017]; archive accessed May 7, 2017).
  2. See, e.g., the Sea FM surf report Archived 2006-05-12 at the Wayback Machine (link dead as of May 8, 2017).
  3. Neal Miyake, "Hawaiian Scale: Measuring Wave Heights in Hawaii," Around Town: Hawaii, May 2003, available at https://web.archive.org/web/20051014143651/http://www.hawaii.rr.com/leisure/reviews/neal_miyake/2003-05_hsmwhihawaii.htm (archived from http://www.hawaii.rr.com:80/leisure/reviews/neal_miyake/2003-05_hsmwhihawaii.htm [link dead as of May 7, 2017]; archive accessed May 7, 2017).
  4. https://web.archive.org/web/20051014143651/http://www.surf-news.com/, archived from http://www.surf-news.com/; archive accessed May 7, 2017
  5. ±0.637 is the approximate result when the integral from 0 to π or from π to 2π of sin(x) is divided by π, the length of the sine wave's half-cycle.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.