Gyroelongated cupola
In geometry, the gyroelongated cupolae are an infinite set of polyhedra, constructed by adjoining an n-gonal cupola to an n-gonal antiprism.
| Set of gyroelongated cupolae | |
|---|---|
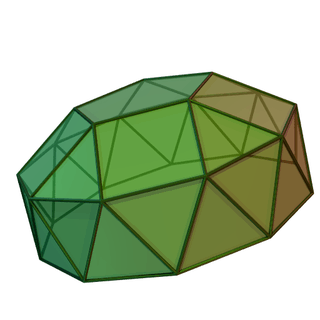 Example pentagonal form | |
| Faces | 3n triangles n squares 1 n-gon 1 2n-gon |
| Edges | 9n |
| Vertices | 5n |
| Symmetry group | Cnv, [n], (*nn) |
| Rotational group | Cn, [n]+, (nn) |
| Dual polyhedron | |
| Properties | convex |
There are three gyroelongated cupolae that are Johnson solids made from regular triangles and square, and pentagons. Higher forms can be constructed with isosceles triangles. Adjoining a triangular prism to a square antiprism also generates a polyhedron, but has adjacent parallel faces, so is not a Johnson solid. The hexagonal form can be constructed from regular polygons, but the cupola faces are all in the same plane. Topologically other forms can be constructed without regular faces.
Forms
| name | faces | |
|---|---|---|
| gyroelongated triangular prism | 2+8 triangles, 2+1 square | |
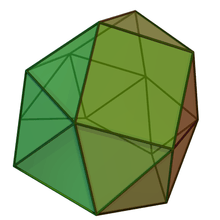 | gyroelongated triangular cupola (J22) | 9+1 triangles, 3 squares, 1 hexagon |
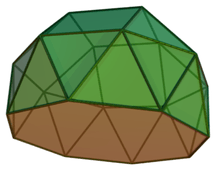 | gyroelongated square cupola (J23) | 12 triangles, 4+1 squares, 1 octagon |
 | gyroelongated pentagonal cupola (J24) | 15 triangles, 5 squares, 1 pentagon, 1 decagon |
| gyroelongated hexagonal cupola | 18 triangles, 6 squares, 1 hexagon, 1 dodecagon |
gollark: "Goodbye".
gollark: GTech™® 14H™ So Cool We Had To Increment G©©© just directly opens wormholes from your device to the base station, then sends QAM-1048576-modulated spatially and frequency-multiplexed X-rays down it.
gollark: Publicly available versions, yes.
gollark: We don't even harvest your soul for it.
gollark: I'm sure LTE does somewhat, but GTech™ 6G™™™ is a bigger number, which is better, and entirely free.
See also
References
- Norman W. Johnson, "Convex Solids with Regular Faces", Canadian Journal of Mathematics, 18, 1966, pages 169–200. Contains the original enumeration of the 92 solids and the conjecture that there are no others.
- Victor A. Zalgaller (1969). Convex Polyhedra with Regular Faces. Consultants Bureau. No ISBN. The first proof that there are only 92 Johnson solids.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.