Decagram (geometry)
In geometry, a decagram is a 10-point star polygon. There is one regular decagram, containing the vertices of a regular decagon, but connected by every third point. Its Schläfli symbol is {10/3}.[1]
| Regular decagram | |
|---|---|
 A regular decagram | |
| Type | Regular star polygon |
| Edges and vertices | 10 |
| Schläfli symbol | {10/3} t{5/3} |
| Coxeter diagram | |
| Symmetry group | Dihedral (D10) |
| Internal angle (degrees) | 72° |
| Dual polygon | self |
| Properties | star, cyclic, equilateral, isogonal, isotoxal |
| Star polygons |
|---|
|
|
The name decagram combines a numeral prefix, deca-, with the Greek suffix -gram. The -gram suffix derives from γραμμῆς (grammēs) meaning a line.[2]
Regular decagram
For a regular decagram with unit edge lengths, the proportions of the crossing points on each edge are as shown below.

Related figures
A regular decagram is a 10-sided polygram, represented by symbol {10/n}, containing the same vertices as regular decagon. Only one of these polygrams, {10/3} (connecting every third point), forms a regular star polygon, but there are also three ten-vertex polygrams which can be interpreted as regular compounds:
- {10/5} is a compound of five degenerate digons 5{2}
- {10/4} is a compound of two pentagrams 2{5/2}
- {10/2} is a compound of two pentagons 2{5}.[4][5]
| Form | Convex | Compound | Star polygon | Compounds | |
|---|---|---|---|---|---|
| Image | 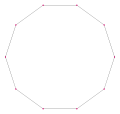 |
.svg.png) |
 |
.svg.png) |
.svg.png) |
| Symbol | {10/1} = {10} | {10/2} = 2{5} | {10/3} | {10/4} = 2{5/2} | {10/5} = 5{2} |
{10/2} can be seen as the 2D equivalent of the 3D compound of dodecahedron and icosahedron and 4D compound of 120-cell and 600-cell; that is, the compound of two pentagonal polytopes in their respective dual positions.
{10/4} can be seen as the two-dimensional equivalent of the three-dimensional compound of small stellated dodecahedron and great dodecahedron or compound of great icosahedron and great stellated dodecahedron through similar reasons. It has six four-dimensional analogues, with two of these being compounds of two self-dual star polytopes, like the pentagram itself; the compound of two great 120-cells and the compound of two grand stellated 120-cells. A full list can be seen at Polytope compound#Compounds with duals.
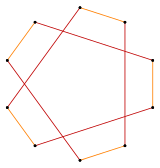
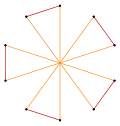
Deeper truncations of the regular pentagon and pentagram can produce intermediate star polygon forms with ten equally spaced vertices and two edge lengths that remain vertex-transitive (any two vertices can be transformed into each other by a symmetry of the figure).[6][7][8]
| Quasiregular | Isogonal | Quasiregular Double covering | |
|---|---|---|---|
 t{5} = {10} |
 |
 |
 t{5/4} = {10/4} = 2{5/2} |
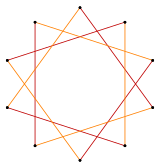 t{5/3} = {10/3} |
 |
 |
 t{5/2} = {10/2} = 2{5} |
References
| Wikimedia Commons has media related to Ten-pointed stars. |
- Barnes, John (2012), Gems of Geometry, Springer, pp. 28–29, ISBN 9783642309649.
- γραμμή, Henry George Liddell, Robert Scott, A Greek-English Lexicon, on Perseus
- Sarhangi, Reza (2012), "Polyhedral Modularity in a Special Class of Decagram Based Interlocking Star Polygons", Bridges 2012: Mathematics, Music, Art, Architecture, Culture (PDF), pp. 165–174.
- Regular polytopes, p 93-95, regular star polygons, regular star compounds
- Coxeter, Introduction to Geometry, second edition, 2.8 Star polygons p.36-38
- The Lighter Side of Mathematics: Proceedings of the Eugène Strens Memorial Conference on Recreational Mathematics and its History, (1994), Metamorphoses of polygons, Branko Grünbaum.
-
- Coxeter, Harold Scott MacDonald; Longuet-Higgins, M. S.; Miller, J. C. P. (1954). "Uniform polyhedra". Philosophical Transactions of the Royal Society of London. Series A. Mathematical and Physical Sciences. The Royal Society. 246 (916): 411. Bibcode:1954RSPTA.246..401C. doi:10.1098/rsta.1954.0003. ISSN 0080-4614. JSTOR 91532. MR 0062446.CS1 maint: ref=harv (link)
- Coxeter, The Densities of the Regular polytopes I, p.43 If d is odd, the truncation of the polygon {p/q} is naturally {2n/d}. But if not, it consists of two coincident {n/(d/2)}'s; two, because each side arises from an original side and once from an original vertex. Thus the density of a polygon is unaltered by truncation.
