Fractal derivative

In applied mathematics and mathematical analysis, the fractal derivative is a non-Newtonian type of derivative in which the variable such as t has been scaled according to t^α. The derivative is defined in fractal geometry.

Physical background

Porous media, aquifers, turbulence, and other media usually exhibit fractal properties. The classical physical laws such as Fick's laws of diffusion, Darcy's law, and Fourier's law are no longer applicable for such media, because they are based on Euclidean geometry, which doesn't apply to media of non-integer fractal dimensions. The basic physical concepts such as distance and velocity in fractal media are required to be redefined; the scales for space and time should be transformed according to (x^β, t^α). The elementary physical concepts such as velocity in a fractal spacetime (x^β, t^α) can be redefined by:

${\displaystyle v'={\frac {dx'}{dt'}}={\frac {dx^{\beta }}{dt^{\alpha }}}\,,\quad \alpha ,\beta >0}$,

where S^α,β represents the fractal spacetime with scaling indices α and β. The traditional definition of velocity makes no sense in the non-differentiable fractal spacetime.

Definition

Based on above discussion, the concept of the fractal derivative of a function u(t) with respect to a fractal measure t has been introduced as follows:

${\displaystyle {\frac {\partial f(t)}{\partial t^{\alpha }}}=\lim _{t_{1}\rightarrow t}{\frac {f(t_{1})-f(t)}{t_{1}^{\alpha }-t^{\alpha }}}\,,\quad \alpha >0}$,

A more general definition is given by

${\displaystyle {\frac {\partial ^{\beta }f(t)}{\partial t^{\alpha }}}=\lim _{t_{1}\rightarrow t}{\frac {f^{\beta }(t_{1})-f^{\beta }(t)}{t_{1}^{\alpha }-t^{\alpha }}}\,,\quad \alpha >0,\beta >0}$.

Motivation

The derivatives of a function f can be defined in terms of the coefficients a_k in the Taylor series expansion:

${\displaystyle f(x)=\sum _{k=1}^{\infty }a_{k}\cdot (x-x_{0})^{k}=\sum _{k=1}^{\infty }{1 \over k!}{d^{k}f \over dx^{k}}(x_{0})\cdot (x-x_{0})^{k}=f(x_{0})+f'(x_{0})\cdot (x-x_{0})+o(x-x_{0})}$

From this approach one can directly obtain:

${\displaystyle f'(x_{0})={f(x)-f(x_{0})-o(x-x_{0}) \over x-x_{0}}=\lim _{x\to x_{0}}{f(x)-f(x_{0}) \over x-x_{0}}}$

This can be generalized approximating f with functions (x^α-(x₀)^α)^k:

${\displaystyle f(x)=\sum _{k=1}^{\infty }b_{k}\cdot (x^{\alpha }-x_{0}^{\alpha })^{k}=f(x_{0})+b_{1}\cdot (x^{\alpha }-x_{0}^{\alpha })+o(x^{\alpha }-x_{0}^{\alpha })}$

note: the lowest order coefficient still has to be b₀=f(x₀), since it's still the constant approximation of the function f at x₀.

Again on can directly obtain:

${\displaystyle b_{1}=\lim _{x\to x_{0}}{f(x)-f(x_{0}) \over x^{\alpha }-x_{0}^{\alpha }}{\overset {\underset {\mathrm {def} }{}}{=}}{df \over dx^{\alpha }}(x_{0})}$

Properties

Expansion coefficients

Just like in the Taylor series expansion, the coefficients b_k can be expressed in terms of the fractal derivatives of order k of f:

${\displaystyle b_{k}={1 \over k!}{\biggl (}{d \over dx^{\alpha }}{\biggr )}^{k}f(x=x_{0})}$

Proof idea: assuming ${\textstyle ({d \over dx^{\alpha }})^{k}f(x=x_{0})}$ exists, b_k can be written written as ${\textstyle b_{k}=a_{k}\cdot ({d \over dx^{\alpha }})^{k}f(x=x_{0})}$

one can now use ${\textstyle f(x)=(x^{\alpha }-x_{0}^{\alpha })^{n}\Rightarrow ({d \over dx^{\alpha }})^{k}f(x=x_{0})=n!\delta _{n}^{k}}$ and since ${\textstyle b_{n}{\overset {\underset {\mathrm {!} }{}}{=}}1\Rightarrow a_{n}={1 \over n!}}$

Connection with Derivative

If for a given function f both the derivative Df and the fractal derivative D_αf exists, one can find an analog to the chain rule:

${\displaystyle {df \over dx^{\alpha }}={df \over dx}{dx \over dx^{\alpha }}={1 \over \alpha }x^{1-\alpha }{df \over dx}}$

The last step is motivated by the Implicit function theorem which, under appropriate conditions, gives us dx/dx^α = (dx^α/dx)⁻¹

Similarly for the more general definition:

${\displaystyle {d^{\beta }f \over d^{\alpha }x}={d(f^{\beta }) \over d^{\alpha }x}={1 \over \alpha }x^{1-\alpha }\beta f^{\beta -1}(x)f'(x)}$

Fractal derivative for function f(t) = t, with derivative order is α ∈ (0,1]

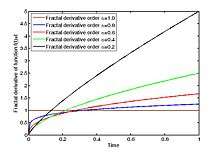
Application in anomalous diffusion

As an alternative modeling approach to the classical Fick’s second law, the fractal derivative is used to derive a linear anomalous transport-diffusion equation underlying anomalous diffusion process,

${\displaystyle {\frac {du(x,t)}{dt^{\alpha }}}=D{\frac {\partial }{\partial x^{\beta }}}\left({\frac {\partial u(x,t)}{\partial x^{\beta }}}\right),-\infty <x<+\infty \,,\quad (1)}$

${\displaystyle u(x,0)=\delta (x).}$

where 0 < α < 2, 0 < β < 1, and δ(x) is the Dirac delta function.

In order to obtain the fundamental solution, we apply the transformation of variables

${\displaystyle t'=t^{\alpha }\,,\quad x'=x^{\beta }.}$

then the equation (1) becomes the normal diffusion form equation, the solution of (1) has the stretched Gaussian form:

${\displaystyle u(x,t)={\frac {1}{2{\sqrt {\pi t^{\alpha }}}}}e^{-{\frac {x^{2\beta }}{4t^{\alpha }}}}}$

The mean squared displacement of above fractal derivative diffusion equation has the asymptote:

${\displaystyle \left\langle x^{2}(t)\right\rangle \propto t^{(3\alpha -\alpha \beta )/2\beta }.}$

Fractal-fractional differentiation and integration

The fractal derivative is connected to the classical derivative if the first derivative of the function under investigation exists. In this case,

${\displaystyle {\frac {\partial f(t)}{\partial t^{\alpha }}}=\lim _{t_{1}\rightarrow t}{\frac {f(t_{1})-f(t)}{t_{1}^{\alpha }-t^{\alpha }}}\ ={\frac {df(t)}{dt}}{\frac {1}{\alpha t^{\alpha -1}}},\quad \alpha >0}$.

However, due to the differentiability property of an integral, fractional derivatives are differentiable, thus the following new concept was introduced

Fractal-fractional differential operators

The following differential operators where introduced and applied very recently .[1]

Definition

Suppose that y(t),be continuous and fractal differentiable on (a, b) with order β then the fractal–fractional derivative of y(t) with order α in the Riemann–Liouville sense having power law type kernel is defined as follows.:[1] ${\displaystyle ^{FFP}D_{0,t}^{\alpha ,\beta }{\Big (}y(t){\Big )}={\dfrac {1}{\Gamma (m-\alpha )}}{\dfrac {d}{dt^{\beta }}}\int _{0}^{t}(t-s)^{m-\alpha -1}y(s)ds}$

Definition

Suppose that y(t) be continuous and the fractal differentiable on (a, b) with order "β" then the fractal–fractional derivative of y(t) with order α in the Riemann–Liouville sense having exponentially decaying type kernel is defined as follows.:[1]

${\displaystyle ^{FFE}D_{0,t}^{\alpha ,\beta }{\Big (}y(t){\Big )}={\dfrac {M(\alpha )}{1-\alpha }}{\dfrac {d}{dt^{\beta }}}\int _{0}^{t}\exp {\Big (}-{\dfrac {\alpha }{1-\alpha }}(t-s){\Big )}y(s)ds}$,

Definition

Suppose that y(t) be continuous and the fractal differentiable on (a, b) with order "β" then the fractal–fractional derivative of y(t) with order α in the Riemann–Liouville sense having generalized Mittag-Leffler type kernel is defined as follows.:[1]

${\displaystyle {}_{a}^{FFM}D_{t}^{\alpha }f(t)={\frac {AB(\alpha )}{1-\alpha }}{\frac {d}{dt^{\beta }}}\int _{a}^{t}f(\tau )E_{\alpha }\left(-\alpha {\frac {\left(t-\tau \right)^{\alpha }}{1-\alpha }}\right)\,d\tau \,.}$

Fractal-fractional integral operators

Fractal-fractional integral operators associate to the new differential operators are given below as.:[1]

Definition

Suppose that y(t) be continuous on an open interval (a, b) then the fractal–fractional integral of y(t) with order α having power law type kernel is defined as follows.:[1]

${\displaystyle ^{FFP}J_{0,t}^{\alpha ,\beta }{\Big (}y(t){\Big )}={\dfrac {\beta }{\Gamma (\alpha )}}\int _{0}^{t}(t-s)^{\alpha -1}s^{\beta -1}y(s)ds}$

Definition

Suppose that y(t) be continuous on an open interval (a, b) then the fractal–fractional integral of y(t) with order α having exponentially decaying type kernel is defined as follows.:[1]

${\displaystyle ^{FFE}J_{0,t}^{\alpha ,\beta }{\Big (}y(t){\Big )}={\dfrac {\alpha \beta }{M(\alpha )}}\int _{0}^{t}s^{\alpha -1}y(s)ds+{\dfrac {\beta (1-\alpha )t^{\beta -1}y(t)}{M(\alpha )}}}$.

Definition

Suppose that y(t) be continuous on an open interval (a, b) then the fractal–fractional integral of y(t) with order α having generalized Mittag-Leffler type kernel is defined as follows .:[1]

${\displaystyle ^{FFM}J_{0,t}^{\alpha ,\beta }{\Big (}y(t){\Big )}={\dfrac {\alpha \beta }{AB(\alpha )}}\int _{0}^{t}s^{\alpha -1}y(s)(t-s)^{\alpha -1}ds+{\dfrac {\beta (1-\alpha )t^{\beta -1}y(t)}{AB(\alpha )}}}$.

FFM is refereed to fractal-fractional with the generalized Mittag-Leffler kernel.

See also

• Fractional calculus
• Fractional-order system
• Multifractal system

References

1. Atangana, Abdon; Sania, Qureshi (2019). "Modeling attractors of chaotic dynamical systems with fractal–fractional operators". Chaos, Solitons & Fractals. 123: 320–337. Bibcode:2019CSF...123..320A. doi:10.1016/j.chaos.2019.04.020.

• Chen, W. (2006). "Time–space fabric underlying anomalous diffusion". Chaos, Solitons and Fractals. 28 (4): 923–929. arXiv:math-ph/0505023. Bibcode:2006CSF....28..923C. doi:10.1016/j.chaos.2005.08.199.
• Kanno, R. (1998). "Representation of random walk in fractal space-time". Physica A. 248 (1–2): 165–175. Bibcode:1998PhyA..248..165K. doi:10.1016/S0378-4371(97)00422-6.
• Chen, W.; Sun, H.G.; Zhang, X.; Korosak, D. (2010). "Anomalous diffusion modeling by fractal and fractional derivatives". Computers and Mathematics with Applications. 59 (5): 1754–8. doi:10.1016/j.camwa.2009.08.020.
• Sun, H.G.; Meerschaert, M.M.; Zhang, Y.; Zhu, J.; Chen, W. (2013). "A fractal Richards' equation to capture the non-Boltzmann scaling of water transport in unsaturated media". Advances in Water Resources. 52 (52): 292–5. Bibcode:2013AdWR...52..292S. doi:10.1016/j.advwatres.2012.11.005. PMC 3686513. PMID 23794783.
• Cushman, J.H.; O'Malley, D.; Park, M. (2009). "Anomalous diffusion as modeled by a nonstationary extension of Brownian motion". Phys. Rev. E. 79 (3): 032101. Bibcode:2009PhRvE..79c2101C. doi:10.1103/PhysRevE.79.032101. PMID 19391995.
• Mainardi, F.; Mura, A.; Pagnini, G. (2010). "The M-Wright Function in Time-Fractional Diffusion Processes: A Tutorial Survey". International Journal of Differential Equations. 2010: 104505. arXiv:1004.2950. Bibcode:2010arXiv1004.2950M. doi:10.1155/2010/104505.

External links

• Power Law & Fractional Dynamics
• Non-Newtonian calculus website