Isotoxal figure
In geometry, a polytope (for example, a polygon or a polyhedron), or a tiling, is isotoxal or edge-transitive if its symmetries act transitively on its edges. Informally, this means that there is only one type of edge to the object: given two edges, there is a translation, rotation and/or reflection that will move one edge to the other, while leaving the region occupied by the object unchanged.
The term isotoxal is derived from the Greek τοξον meaning arc.
Isotoxal polygons
An isotoxal polygon is an equilateral polygon, but not all equilateral polygons are isotoxal. The duals of isotoxal polygons are isogonal polygons.
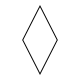
In general, an isotoxal 2n-gon will have Dn (*nn) dihedral symmetry. A rhombus is an isotoxal polygon with D2 (*22) symmetry.
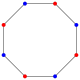
All regular polygons (equilateral triangle, square, etc.) are isotoxal, having double the minimum symmetry order: a regular n-gon has Dn (*nn) dihedral symmetry. A regular 2n-gon is an isotoxal polygon and can be marked with alternately colored vertices, removing the line of reflection through the mid-edges.
| D2 (*22) | D3 (*33) | D4 (*44) | D5 (*55) | |||||
|---|---|---|---|---|---|---|---|---|
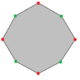
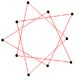
| Rhombus | Equilateral triangle | Concave hexagon | Self-intersecting hexagon | Convex octagon | Regular pentagon | Self-intersecting (regular) pentagram | Self-intersecting decagram | |
 |
 |
 |
 |
 |
 |
 |
 |
 |
Isotoxal polyhedra and tilings
Regular polyhedra are isohedral (face-transitive), isogonal (vertex-transitive) and isotoxal. Quasiregular polyhedra, like the cuboctahedron and icosidodecahedron, are isogonal and isotoxal, but not isohedral. Their duals, including the rhombic dodecahedron and the rhombic triacontahedron, are isohedral and isotoxal, but not isogonal.
| Quasiregular polyhedron |
Quasiregular dual polyhedron |
Quasiregular star polyhedron |
Quasiregular dual star polyhedron |
Quasiregular tiling |
Quasiregular dual tiling |
|---|---|---|---|---|---|
 A cuboctahedron is an isogonal and isotoxal polyhedron |
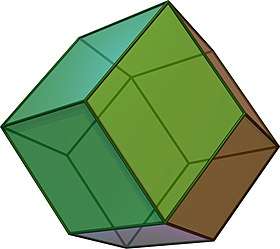 A rhombic dodecahedron is an isohedral and isotoxal polyhedron |
 A great icosidodecahedron is an isogonal and isotoxal star polyhedron |
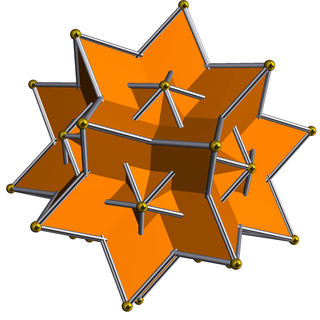 A great rhombic triacontahedron is an isohedral and isotoxal star polyhedron |
 The trihexagonal tiling is an isogonal and isotoxal tiling |
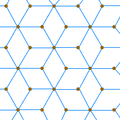 The rhombille tiling is an isohedral and isotoxal tiling with p6m (*632) symmetry. |
Not every polyhedron or 2-dimensional tessellation constructed from regular polygons is isotoxal. For instance, the truncated icosahedron (the familiar soccerball) has two types of edges: hexagon-hexagon and hexagon-pentagon, and it is not possible for a symmetry of the solid to move a hexagon-hexagon edge onto a hexagon-pentagon edge.
An isotoxal polyhedron has the same dihedral angle for all edges.
There are nine convex isotoxal polyhedra formed from the Platonic solids, eight formed from the Kepler–Poinsot polyhedra, three more as quasiregular ditrigonal (3 | p q) star polyhedra, and three more as their duals.
There are at least 5 polygonal tilings of the Euclidean plane that are isotoxal, and infinitely many isotoxal polygonal tilings of the hyperbolic plane, including the Wythoff constructions from the regular hyperbolic tilings {p,q}, and non-right (p q r) groups.
References
- Peter R. Cromwell, Polyhedra, Cambridge University Press 1997, ISBN 0-521-55432-2, p. 371 Transitivity
- Grünbaum, Branko; Shephard, G. C. (1987). Tilings and Patterns. New York: W. H. Freeman. ISBN 0-7167-1193-1. (6.4 Isotoxal tilings, 309-321)
- Coxeter, Harold Scott MacDonald; Longuet-Higgins, M. S.; Miller, J. C. P. (1954), "Uniform polyhedra", Philosophical Transactions of the Royal Society of London. Series A. Mathematical and Physical Sciences, 246: 401–450, doi:10.1098/rsta.1954.0003, ISSN 0080-4614, JSTOR 91532, MR 0062446