C-squares

C-squares (acronym for the concise spatial query and representation system) is a system of spatially unique, location-based identifiers (geocodes) for areas on the surface of the earth, represented as cells from a Discrete Global Grid at a hierarchical set of resolution steps. The identifiers incorporate literal values of latitude and longitude in an interleaved notation (producing grid resolutions of 10, 1, 0.1 degrees, etc.), together with additional digits that support intermediate grid resolutions of 5, 0.5, 0.05 degrees, etc. The system was initially designed to represent data "footprints" or spatial extents in a more flexible manner than a standard minimum bounding rectangle, and to support "lightweight", text-based spatial querying; it can also provide a set of identifiers for grid cells used for assembly, storage and analysis of spatially organised data. Dataset extents expressed in c-squares notation can be visualised using a web-based utility, the c-squares mapper, an online instance of which is currently provided by CSIRO Oceans and Atmosphere in Australia. C-squares codes and associated published software are free to use and the software is released under version 2 of the GNU General Public License (GPL), a licence of the Free Software Foundation.

C-squares
Full nameConcise spatial query and representation system
OrganisationCSIRO
Introduced1 May 2002 (2002-05-01)
No. issuedresolution dependent, e.g.:
648 (10 degree squares),
2,592 (5 degree squares),
64,800 (1 degree squares),
259,200 (0.5 degree squares)
No. of digitsresolution dependent, e.g.:
4 (10 degree squares),
6 (5 degree squares),
8 (1 degree squares),
10 (0.5 degree squares) (counts include separator character/s)
Example3112 (10 degree square),
3112:3 (5 degree square),
3112:360 (1 degree square),
3112:360:4 (0.5 degree square)
Websitecsquares.sourceforge.net,
www.cmar.csiro.au/csquares/

History

The c-squares method was developed by Tony Rees at CSIRO Oceans and Atmosphere in Australia (then "CSIRO Marine Research") in 2001-2, initially as a method for spatial indexing, rapid query, and compact storage and visualization of dataset spatial "footprints" in an agency-specific metadata directory (data catalogue).[1][2] It was later published in the scientific literature as a freely available tool for use by other workers, together with a web-accessible mapping utility entitled the "c-squares mapper" for visualisation of data extents expressed in the c-squares notation.[3] Since that time, a number of projects and international collaborations have employed c-squares to support spatial indexing and/or map production, including Fishbase (to map stored data points for any species), the Ocean Biogeographic Information System (OBIS),[4][5] AquaMaps,[6] data analysis to support the designation of marine biogeographic realms,[7] for multi-national fisheries data collation by the Scientific, Technical and Economic Committee for Fisheries (STECF) of the European Commission,[8], and for data reporting by ICES.[9] For its application in displaying and modelling global biodiversity data, c-squares was one of four components cited in the award of the Ebbe Nielsen Prize to Rees by the Global Biodiversity Information Facility (GBIF) in 2014.[10] The concept of representing dataset "footprints" as cells of spatial data of this nature and alignment has been stated to have been inspired by the data addressing method in the U.S. National Oceanographic Data Center (NODC) "World Ocean Database" product,[11][1] which uses 10 degree World Meteorological Organization squares (the starting point for c-squares hierarchical subdivision) for organising its data content, and the set of 1:100,000 topographic maps issued by the national mapping agency for Australia (coverage and index here); each map covers a 0.5 degree square and, with its associated mapsheet labels, can notionally be used as a unit of spatial identification.[1]

Rationale

Indexing spatial data
Main article: Grid (spatial index)

Spatial data are inherently (at least) 2-dimensional; without additional indexing, a numeric range query in 2 dimensions (e.g. x and y, or latitude and longitude) is required to retrieve data items within a particular area. Such queries are computationally expensive so it can be beneficial to pre-process (index) the data in some manner that reduces the inherent dimensionality from two to one dimension, for example as labelled cells of a grid; the grid labels can then be indexed by standard, one dimensional methods for rapid search and retrieval,[12] and/or searched by simple alphanumeric text searches. C-squares is an example of such a grid where the cell identifiers are designed to be human- as well as machine-readable, and to be concordant with recognizable and commonly intervals of latitude and longitude.

Dataset footprints

Spatial data, that is, data associated with particular geographic locations on the earth, have spatial "footprints" that ideally are recorded in metadata systems or data catalogues, to support spatial searching of the resources in question.[13] A "basic" generalization of any data footprint is the minimum bounding rectangle or MBR, that is, the smallest set of boundaries of latitude and longitude that completely contain the data. Such stored rectangles are relatively simple to query as a mathematical operation (look for overlap with an input "search" rectangle) but, with real world data, may not be a good surrogate for the true data "footprint" if the latter contains disjoint or sparsely populated data items, items on a diagonal line, or items with significant "holes", such as a vessel track around a continent.[3] Representation as a set of smaller "tiles", such those denoted by c-square codes at an appropriate resolution, can more accurately reflect the shape of such non-rectangular and/or non-contiguous datasets.[3][13]

Data binning
Main article: Data binning

"Binning" describes the process of converting continuously variable data (in the present case, spatial locations in degrees of latitude and longitude) into a set of discrete "bins" in order to apply the indexing and subsequent search/retrieval processes, other processing and reporting, etc. The optimal size of the spatial data "bins" can depend on the user's requirements (e.g. geographic coverage), desire for handling large vs. small datasets (which can affect the time required for processing or production of on-demand maps) and density of available data (with sparse input data, many "bins" may end up being empty). Large "bins" will have smaller data handling requirements and smooth out data deficiencies, but will result in a loss of resolution of fine scale data; small "bins" can result in large quantities of data to be handled (for example, a global coverage at 0.1 degree resolution requires over 6 million grid cells) which may be too much for easy handling. To date, 0.5 degree cells (50×50 km nominal size) have been found to be a reasonable compromise between resolution and data storage requirements for global coverages (259,200 cells), e.g. as used for Aquamaps,[6] while for more local applications, either 0.5 or 0.1 degree cells may be useful.

Data reduction
Main article: data reduction

One advantage of binning spatial data as described above is that it offers the potential for data reduction in some use cases: for example rather than storing (say) hundreds of raw data points within the same bin, the data can be represented as an average value and/or number of data points held, or just as presence/absence (for example as a range map). By this means, the quantity of information required to be stored in the spatial index and associated information can be substantially reduced in many cases, with a concomitant improvement in performance (speed of spatial queries and result mapping as desired).

Hierarchical representation
Main article: Discrete global grid § Hierarchical grids

As a property of a discrete global grid, hierarchical notation ensures that the geocodes for finer resolutions of the mesh incorporate those of all their parents, permitting rapid search and/or data aggregation at any desired equal or higher level of the hierarchy. In the c-squares case, the code is extended by additional alphanumeric characters as the spatial resolution increases, with the corollary that resolution can be decreased if desired, merely by truncating the code by the relevant amount.

An equal angle spherical (global) grid, represented in a "real world" (orthographic) perspective.

Equal angle grids

Equal angle grids (the class that includes c-squares) have the advantage that transformation of spatial data (for example as simple coordinates of latitude and longitude) in and out of the grid notation can be simple, since the latitude–longitude grid is itself equal angle.[14] On the actual surface of the globe, the cells are approximately "square" only adjacent to the equator, and become progressively narrower and tapered (also with curved northern and southern boundaries) as they approach the poles, and cells adjoining the poles are unique in possessing three faces rather than four. By contrast, equal area grids attempt to preserve a constant area for all cells at the same hierarchical level (resolution), at the expense of losing concordance with familiar lines of latitude and/or longitude.

Regional (local/national) vs. global grids

Local and/or national grids have been developed for use within a number of countries, for example the UK National Grid has been in use since 1946,[15] while a separate system is in use for Ireland. Discontinuities occur where such grids meet or overlap, and some areas (for example the more offshore portions of surrounding seas and the Channel Islands) are not covered at all. Global grids offer a solution to this problem (providing standard treatment for all areas of the globe) and also offer a potential format for collation of cross-national data into a single repository for analysis and reporting, for example see Vanhee et al., 2018.[8]

The c-squares global grid notation
Global coverage of 10x10 degree World Meteorological Organization (WMO) squares (= c-squares 10-degree grid)

Initial 10 degree squares

10-degree c-squares are specified as being identical to equivalent World Meteteorological Organization (WMO) square codes, refer illustration at right. These squares are aligned with 10-degree subdivisions of the global latitude–longitude grid, which for c-squares use is specified as employing the WGS84 datum. WMO (10 degree) squares are encoded with four digits, in the series 1xxx, 3xxx, 5xxx and 7xxx.[11] The leading digit indicates the "global quadrant" with 1 for north-east (latitude and longitude are both positive), 3 for south-east (latitude is negative and longitude positive), 5 for south-west (latitude and longitude are both negative) and 7 for north-west (latitude is positive and longitude negative). The next digit, 0 through 8, corresponds to the tens of latitude degrees either north or south; while the remaining 2 digits, 00 through 17, correspond to the tens of longitude degrees either east or west (by specification, 0 is treated as positive). Thus the 10 degree cell with its lower left corner at 0,0 (latitude,longitude) is encoded 1000, and acts as a bin to contain all spatial data between 0 and 10 degrees north (actually, 0 and 9.999...) and 0 and 9.999... degrees east; the 10 degree cell with its lower left corner at 80 N, 170 E is encoded 1817, and acts as a bin to contain all spatial data between 80 and 90 degrees north and 170 and 179.999... degrees east.

Subsequent recursive subdivision

C-squares extends the initial WMO 10×10 square notation via a recursive series of "cycles", each 3 digits long (the final one may be 1 digit), separated by the colon character, the number of characters (and cycles) indicating the resolution encoded, as per these examples:

  • 1000 ... 10×10 degree square (up to 1000×1000 km nominal)
  • 1000:1 ... 5×5 degree square (up to 500×500 km nominal)
  • 1000:100 ... 1×1 degree square (up to 100×100 km nominal)
  • 1000:100:1 ... 0.5×0.5 degree square (up to 50×50km nominal)
  • 1000:100:100 ... 0.1×0.1 degree square (up to 10×10 km nominal)
  • 1000:100:100:1 ... 0.05×0.05 degree square (up to 5×5km nominal)

(etc.)

The nominal sizes given reflect the fact that at the equator, 1 degree of both latitude and longitude correspond to around 110 km, with the actual value for longitude declining between there and the poles, where it becomes zero (latitude actual: 110.567 km at the equator, 111.699 km at the poles; longitude actual: 111.320 km at the equator, 78.847 km at latitude ±45 degrees, 0 km at the poles); at a sample northern hemisphere latitude e.g. that of London (51.5 degrees north), a 1×1 degree square measures approximately 111×69 km.[16]

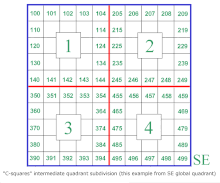
C-squares recursive subdivision principle - intermediate quadrant example (south-east global quadrant)

To produce the 1 or 3 digits in any cycle following the initial 4-digit, 10-degree square identifier, first an "intermediate quadrant", 1 through 4 is designated (refer diagram at right), where 1 indicates low absolute values of both latitude and longitude (regardless of sign), 2 indicates low longitude and high latitude, 3 indicates high latitude and low longitude, and 4 indicates high values for both; "low" and high" being taken from the relevant portion of the data to be gridded (for example within the 10 degree cell extending from 10 to 20 degrees, 10 is treated as low and 19 as high). This leading digit in a cycle is then followed simply by the next applicable digit for first latitude and then longitude: thus an input value of latitude +11.0, longitude +12.0 degrees will be encoded as the 5 degree c-square code 1101:1 and the 1 degree code 1101:112. Inspection of this code will show that the input latitude value can be recovered directly from the digits 1101:112 while the longitude is included as 1101:112; the sign for these is both positive, as indicated by the first digit of the leading 4 (1 in this case, indicating the north east global quadrant).

From 2002 onwards (still current at 2020), an online "latlong to c-squares conversion page" is available at the website of CSIRO Marine Research (now CSIRO Oceans and Atmosphere) which will convert input values of latitude and longitude to the equivalent c-square code at user selectable resolutions from 10 to 0.1 degree cell size. Alternatively it is a comparatively simple task to program from first principles (or construct as, for example, a Microsoft Excel worksheet) according to the c-squares specification;[17] an example is available here.

C-squares strings, and the c-squares mapper

A set of c-squares (contiguous or non contiguous) can be represented as a concatenated list of individual square codes, separated by the "pipe" (|) character, thus: 7500:110:3|7500:110:1|1500:110:3|1500:110:1 (etc.). This set of squares can then serve as an indication of a dataset extent, similar in function (but simpler to specify) to a MultiPolygon in the Well-known text representation of geometry, the functional difference being that defined points forming the boundary of a polygon can be continuously variable, while those for the c-square boundaries are constrained to fixed intervals from the grid square resolution in use. If these strings are stored, for example as "long text" within a field of a conventional text storage system (e.g. spreadsheet, database, etc.) they can be used for the operation of spatial searches (see following section/s).

C-squares strings can also be used directly as input to an instance of the "c-squares mapper", a web-based utility in operation since 2002 at CSIRO in Australia (under the domain obis.org.au) and also at other global locations. To visualize the position of any set of squares on a map, the current syntax to address an installation of the "c-squares mapper" is (e.g.):

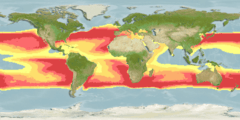
http://www.obis.org.au/cgi-bin/cs_map.pl?csq=3211:123:2|3211:113:4|3211:114:1|3211:206:2|3211:206:1|3111:496:3|3111:495:4|3111:495:1|3111:394:2|3111:495:2|3111:384:3|3111:383:1|3111:382:2|3111:372:3|3111:371:4|3112:371:1|3111:370:2| (etc.).

AquaMap for Mola mola, the ocean sunfish, generated via the c-squares mapper at 0.5 degree square resolution

It should be noted here that the above call to the c-squares mapper is a simple one, with only a single parameter (a single c-squares string) which produces a simple "default map"; the mapper is in fact quite highly customizable, capable of accepting up to seven c-squares strings concurrently, plotting them in user-specified colours, with a choice of empty of filled squares, user-selectable base map, etc. etc.; a full list of available input parameters is provided on the mapper "technical information" page.[18] A more sophisticated map produced using a larger number of available parameters is the colour-coded example at right (AquaMap, i.e. modelled distribution, for the ocean sunfish).

Spatial searching

In a system that uses c-squares codes as units of spatial indexing, a text-based search on any of these square identifiers will retrieve data associated with the relevant square. If a wildcard search is supported (for example in the case that the wildcard character is a percent sign), a search on "7500%" will retrieve all data items in that ten degree square, a search on "7500:1%" will retrieve all data items in that five degree square, etc.

The asterisk character "*" has a special (reserved) meaning in c-squares notation, being a "compact" notation indicating that all finer cells within a higher level cell are included, to the level of resolution indicated by the number of asterisks. In the example above, "7500:*" would indicate that all 4 five-degree cells within parent ten-degree cell "7500" are filled, "7500:***" would indicate that all 100 one-degree cells within parent ten-degree cell "7500" are filled, etc. This approach enables the filling of contiguous blocks of cells with an economy of characters in many cases (a form of data compression), that is useful for efficient storage and transfer of c-squares codes as required.

Spatial data exchange, assembly, and analysis

Examples of the use of c-squares for multi-national data reporting, assembly and analysis include the use of 0.05 × 0.05 degree c-squares for VMS (vessel monitoring systems) data and fishing logbook data for ICES, the International Council for the Exploration of the Sea and others,[9][19] identification of vulnerable marine ecosystems in the North-East Atlantic,[20] and the reporting and collation of fishing activity by member states into 0.5 × 0.5 degree c-squares by the Scientific, Technical and Economic Committee for Fisheries (STECF) of the European Commission.[8][21] The marine species distribution modelling project "AquaMaps" makes available its base data coverages of global marine environmental variables as c-squares gridded data at 0.5 degree resolution.[22]

Licensing and software availability

There is no licence required to use the c-squares method, which has been openly published in the scientific literature since 2003. Source code for the mapper, etc., available via the SourceForge website, is released under the GNU General Public License version 2.0 (GPLv2), which provides free use and redistribution, and subsequent modification for any purpose so long as that licence is retained with the product and any subsequent modifications, in other words, that all the released improved versions will also be free software.[23]

gollark: <:p_mosfet:798503052012552202>
gollark: ++magic py await ctx.send("Bee")
gollark: ++magic py print("bee")
gollark: ++magic py return 5
gollark: ++magic sql select * from sqlite_master;

See also

References
  1. CSIRO Marine Research, 2002: About C-Squares.
  2. Rees, Tony (2002): "C-squares–a new metadata element for improved spatial querying and representation of spatial dataset coverage in metadata records". Proceedings of EOGEO Technical Workshop May 2002, Ispra, Italy.
  3. Rees, Tony (2003). "'C-squares', a new spatial indexing system and its applicability to the description of oceanographic datasets". Oceanography. 16 (1): 11–19. doi:10.5670/oceanog.2003.52.
  4. Tony Rees and Phoebe Zhang, 2007. "Evolving concepts in the architecture and functionality of OBIS, the Ocean Biogeographic Information System". in Vanden Berghe, E. et al. (ed.) Proceedings of Ocean Biodiversity Informatics: an international conference on marine biodiversity data management Hamburg, Germany, 29 November-1 December, 2004. IOC Workshop Report, 202, VLIZ Special Publication 37: pp. 167-176.
  5. Fujioka, Ei; Vanden Berghe, Edward; Donnelly, Ben; et al. (2012). "Advancing global marine biogeography research with open-source GIS software and cloud computing". Transactions in GIS. 16 (2): 143–160. doi:10.1111/j.1467-9671.2012.01310.x.
  6. Ready, Jonathan; Kaschner, Kristin; South, Andy B.; et al. (2010). "Predicting the distributions of marine organisms at the global scale". Ecological Modelling. 221 (3): 467–478. doi:10.1016/j.ecolmodel.2009.10.025.
  7. Costello, Mark J.; Tsai, Peter; Wong, Pui Shan; Cheung, Alan Kwok Lun; Basher, Zeenatul; Chaudhary, Chhaya (2017). "Marine biogeographic realms and species endemicity". Nature Communication. 8 (3): article 1057. doi:10.1038/s41467-017-01121-2. PMC 5648874. PMID 29051522.
  8. Willy Vanhee, Arina Motova & Antonella Zanzi (eds) (2018). Scientific, Technical and Economic Committee for Fisheries - 59th Plenary Meeting Report (PLEN-18-03). Publications Office of the European Union, Luxembourg, 95 pp. ISBN 978-92-79-98374-0, doi:10.2760/335280
  9. International Council for the Exploration of the Sea (2019) ICES Technical Guidelines: 16.3.3.3 Spatial distribution of fishing effort and physical disturbance of benthic habitats by mobile bottom trawl fishing gear using VMS. doi: 10.17895/ices.advice.4683 1 Available at https://www.ices.dk/sites/pub/Publication%20Reports/Guidelines%20and%20Policies/16.03.03.03_Guidelines_Vessel_Monitoring_Systems_Data.pdf
  10. gbif.org, News, 13 July 2014: CSIRO’s Tony Rees named 2014 Ebbe Nielsen Prize winner
  11. U.S. National Oceanographic Data Centre, 1998: "World Ocean Database 1998: Documentation and Quality Control, Version 1.2." Appendix 10A: World Meteorological Organization (WMO) Squares for the Atlantic and Indian Oceans; Appendix 10B: World Meteorological Organization (WMO) Squares for the Pacific Ocean.
  12. Rigaux, P., Scholl, M., and Voisard, A. 2002. Spatial Databases - with application to GIS. Morgan Kaufmann, San Francisco, 410pp.
  13. Hill, Linda (2006). Georeferencing: The Geographic Associations of Information. MIT Press, Cambridge, Mass. and London, England, 260 pp. ISBN 978-0-262-08354-6
  14. Kimerling, A. Jon; Sahr, Kevin; White, Denis; Song, Lian (1999). "Comparing geometrical properties of global grids". Cartography and Geographic Information Science. 26 (4): 271–288. doi:10.1559/152304099782294186. S2CID 123180711.
  15. Anonymous (1946). "The National Grid of the Ordnance Survey". Nature. 158 (4015): 510. doi:10.1038/158510a0.
  16. U.S. National Hurricane Center and Central Pacific Hurricane Center: Latitude/Longitude Distance Calculator
  17. C-squares Specification - Version 1.1 (December 2005)
  18. CMAR c-squares Mapper - Technical Information page
  19. Schulte, K. F.; Siegel, V.; Hufnagl, M.; Schulze, M.; Temming, A. (2020). "Spatial and temporal distribution patterns of brown shrimp (Crangon crangon) derived from commercial logbook, landings, and vessel monitoring data". ICES Journal of Marine Science. 77 (3): 1017–1032. doi:10.1093/icesjms/fsaa021.
  20. Morato, Telmo; Pham, Christopher K.; Pinto, Carlos; Golding, Neil; Ardron, Jeff A.; Muñoz, Pablo Durán; Neat, Francis (2018). "A multi criteria assessment method for identifying vulnerable marine ecosystems in the North-East Atlantic". Frontiers in Marine Science. 5: 460. doi:10.3389/fmars.2018.00460.
  21. Holmes, S.J., Gibin, M., Scott, F., Zanzi, A., et al. (2018). Report on the STECF Expert Working Group 17-12 Fisheries Dependent Information: 'New-FDI', EUR 29204 EN, European Union, Luxembourg. ISBN 978-92-79-85241-1, doi:10.2760/094412. Available at https://publications.jrc.ec.europa.eu/repository/bitstream/JRC111443/jrc_technical_report_stecf-17-12_new-fdi_final_1.pdf
  22. Kesner-Reyes, K., Segschneider, J., Garilao, C., Schneider, B., Rius-Barile, J., Kaschner, K. and Froese, R. (editors). AquaMaps Environmental Dataset: Half-Degree Cells Authority File (HCAF). World Wide Web electronic publication, www.aquamaps.org/main/envt_data.php, ver. 7, 10/2019. (announced; previous versions available for download via https://www.aquamaps.org/main/envt_data.php).
  23. Free Software Foundation: Frequently Asked Questions about version 2 of the GNU GPL
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.