Function composition

In mathematics, function composition is an operation that takes two functions $f$ and $g$ and produces a function $h$ such that $h (x) = g (f (x))$ . In this operation, the function $g$ is applied to the result of applying the function $f$ to $x$ . That is, the functions $f : X \to Y$ and $g : Y \to Z$ are composed to yield a function that maps $x$ in $X$ to $g (f (x))$ in $Z$ .

Intuitively, if $z$ is a function of $y$ , and $y$ is a function of $x$ , then $z$ is a function of $x$ . The resulting composite function is denoted $g \circ f : X \to Z$ , defined by $(g \circ f)(x) = g (f (x))$ for all $x$ in $X$ .[nb 1] The notation $g \circ f$ is read as " $g$ circle $f$ ", " $g$ round $f$ ", " $g$ about $f$ ", " $g$ composed with $f$ ", " $g$ after $f$ ", " $g$ following $f$ ", " $g$ of $f$ ", " $f$ then $g$ ", or " $g$ on $f$ ". Intuitively, composing functions is a chaining process in which the output of function $f$ feeds the input of function $g$ .

The composition of functions is a special case of the composition of relations, so all properties of the latter are true of composition of functions.[1] The composition of functions has some additional properties.

Examples

Concrete example for the composition of two functions.

Composition of functions on a finite set: If $f = {(1, 1), (2, 3), (3, 1), (4, 2)}$ , and $g = {(1, 2), (2, 3), (3, 1), (4, 2), }$ , then $g \circ f = {(1, 2), (2, 1), (3, 2), (4, 3)}$ ; see graphic of concrete example on right.
Composition of functions on an infinite set: If $f : ℝ \to ℝ$ (where $ℝ$ is the set of all real numbers) is given by $f (x) = 2 x + 4$ and $g : ℝ \to ℝ$ is given by $g (x) = x 3$ , then:

(f \circ g)(x) = f (g (x)) = f (x 3) = 2 x 3 + 4

, and

(g \circ f)(x) = g (f (x)) = g (2 x + 4) = (2 x + 4) 3

.

If an airplane's altitude at time $t$ is given by the function $a (t)$ , and the air pressure at altitude $x$ is given by the function $p (x)$ , then $(p \circ a)(t)$ describes the pressure around the plane at time $t$ .

Properties

The composition of functions is always associative—a property inherited from the composition of relations.[1] That is, if $f$ , $g$ , and $h$ are three functions with suitably chosen domains and codomains, then $f \circ (g \circ h) = (f \circ g) \circ h$ , where the parentheses serve to indicate that composition is to be performed first for the parenthesized functions. Since there is no distinction between the choices of placement of parentheses, they may be left off without causing any ambiguity.

In a strict sense, the composition $g \circ f$ can be built only if the codomain of $f$ equals the domain of $g$ ; in a wider sense it is sufficient that the former be a subset of the latter.[nb 2] Moreover, it is often convenient to tacitly restrict the domain of $f$ such that $f$ produces only values in the domain of $g$ ; for example, the composition $g \circ f$ of the functions $f : ℝ \to (-\infty,+9]$ defined by $f (x) = 9 - x 2$ and $g : [0,+\infty) \to ℝ$ defined by $g (x) = \sqrt x$ can be defined on the interval $[-3,+3]$ .

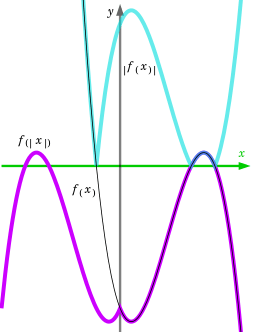
Compositions of two real functions, the absolute value and a cubic function, in different orders, show a non-commutativity of composition.

The functions $g$ and $f$ are said to commute with each other if $g \circ f = f \circ g$ . Commutativity is a special property, attained only by particular functions, and often in special circumstances. For example, $| x | + 3 = | x + 3 |$ only when $x \geq 0$ . The picture shows another example.

The composition of one-to-one functions is always one-to-one. Similarly, the composition of onto functions is always onto. It follows that the composition of two bijections is also a bijection. The inverse function of a composition (assumed invertible) has the property that $(f \circ g) -1 = g -1 \circ f -1$ .[2]

Derivatives of compositions involving differentiable functions can be found using the chain rule. Higher derivatives of such functions are given by Faà di Bruno's formula.

Composition monoids

Suppose one has two (or more) functions $f : X \to X,$ $g : X \to X$ having the same domain and codomain; these are often called transformations. Then one can form chains of transformations composed together, such as $f \circ f \circ g \circ f$ . Such chains have the algebraic structure of a monoid, called a transformation monoid or (much more seldom) a composition monoid. In general, transformation monoids can have remarkably complicated structure. One particular notable example is the de Rham curve. The set of all functions $f : X \to X$ is called the full transformation semigroup[3] or symmetric semigroup[4] on $X$ . (One can actually define two semigroups depending how one defines the semigroup operation as the left or right composition of functions.[5])

The similarity that transforms triangle EFA into triangle ATB is the composition of a homothety

H

and a rotation

R

, of which the common centre is S. For example, the image of A under the rotation

R

is U, which may be written

R

(A) = U. And

H

(U) = B means that the mapping

H

transforms U into B. Thus

H (R

(A)) =

(H \circ R)

(A) = B.

If the transformations are bijective (and thus invertible), then the set of all possible combinations of these functions forms a transformation group; and one says that the group is generated by these functions. A fundamental result in group theory, Cayley's theorem, essentially says that any group is in fact just a subgroup of a permutation group (up to isomorphism).[6]

The set of all bijective functions $f : X \to X$ (called permutations) forms a group with respect to function composition. This is the symmetric group, also sometimes called the composition group.

In the symmetric semigroup (of all transformations) one also finds a weaker, non-unique notion of inverse (called a pseudoinverse) because the symmetric semigroup is a regular semigroup.[7]

Functional powers

If $Y \subseteq X$ , then $f : X \to Y$ may compose with itself; this is sometimes denoted as $f 2$ . That is:

(f \circ f)(x) = f (f (x)) = f 2 (x)

(f \circ f \circ f)(x) = f (f (f (x))) = f 3 (x)

(f \circ f \circ f \circ f)(x) = f (f (f (f (x)))) = f 4 (x)

More generally, for any natural number $n \geq 2$ , the $n$ th functional power can be defined inductively by $f n = f \circ f n -1 = f n -1 \circ f$ , a notation introduced by Hans Heinrich Bürmann[8][9] and John Frederick William Herschel.[10][8][11][9] Repeated composition of such a function with itself is called iterated function.

By convention, $f 0$ is defined as the identity map on $f$ 's domain, $id X$ .
If even $Y = X$ and $f : X \to X$ admits an inverse function $f -1$ , negative functional powers $f - n$ are defined for $n > 0$ as the negated power of the inverse function: $f - n = (f -1) n$ .[10][8][9]

Note: If $f$ takes its values in a ring (in particular for real or complex-valued $f$ ), there is a risk of confusion, as $f n$ could also stand for the $n$ -fold product of $f$ , e.g. $f 2 (x) = f (x) \cdot f (x)$ .[9] For trigonometric functions, usually the latter is meant, at least for positive exponents.[9] For example, in trigonometry, this superscript notation represents standard exponentiation when used with trigonometric functions: $sin 2 (x) = sin(x) \cdot sin(x)$ . However, for negative exponents (especially −1), it nevertheless usually refers to the inverse function, e.g., $tan -1 = arctan \neq 1/tan$ .

In some cases, when, for a given function $f$ , the equation $g \circ g = f$ has a unique solution $g$ , that function can be defined as the functional square root of $f$ , then written as $g = f 1/2$ .

More generally, when $g n = f$ has a unique solution for some natural number $n > 0$ , then $f m / n$ can be defined as $g m$ .

Under additional restrictions, this idea can be generalized so that the iteration count becomes a continuous parameter; in this case, such a system is called a flow, specified through solutions of Schröder's equation. Iterated functions and flows occur naturally in the study of fractals and dynamical systems.

To avoid ambiguity, some mathematicians choose to use $\circ$ to denote the compositional meaning, writing $f \circ n (x)$ for the $n$ -th iterate of the function $f (x)$ , as in, for example, $f \circ3 (x)$ meaning $f (f (f (x)))$ . For the same purpose, $f [n] (x)$ was used by Benjamin Peirce[12][9] whereas Alfred Pringsheim and Jules Molk suggested $n f (x)$ instead.[13][9][nb 3]

Alternative notations

Many mathematicians, particularly in group theory, omit the composition symbol, writing $gf$ for $g \circ f$ .[14]

In the mid-20th century, some mathematicians decided that writing " $g \circ f$ " to mean "first apply $f$ , then apply $g$ " was too confusing and decided to change notations. They write " $xf$ " for " $f (x)$ " and " $(xf) g$ " for " $g (f (x))$ ".[15] This can be more natural and seem simpler than writing functions on the left in some areas – in linear algebra, for instance, when $x$ is a row vector and $f$ and $g$ denote matrices and the composition is by matrix multiplication. This alternative notation is called postfix notation. The order is important because function composition is not necessarily commutative (e.g. matrix multiplication). Successive transformations applying and composing to the right agrees with the left-to-right reading sequence.

Mathematicians who use postfix notation may write " $fg$ ", meaning first apply $f$ and then apply $g$ , in keeping with the order the symbols occur in postfix notation, thus making the notation " $fg$ " ambiguous. Computer scientists may write " $f; g$ " for this,[16] thereby disambiguating the order of composition. To distinguish the left composition operator from a text semicolon, in the Z notation the ⨾ character is used for left relation composition.[17] Since all functions are binary relations, it is correct to use the [fat] semicolon for function composition as well (see the article on composition of relations for further details on this notation).

Composition operator

Given a function $g$ , the composition operator $C g$ is defined as that operator which maps functions to functions as

C_{g}f=f\circ g.

Composition operators are studied in the field of operator theory.

In programming languages

Function composition appears in one form or another in numerous programming languages.

Multivariate functions

Partial composition is possible for multivariate functions. The function resulting when some argument $x i$ of the function $f$ is replaced by the function $g$ is called a composition of $f$ and $g$ in some computer engineering contexts, and is denoted $f | x i = g$

f|_{x_{i}=g}=f(x_{1},\ldots ,x_{i-1},g(x_{1},x_{2},\ldots ,x_{n}),x_{i+1},\ldots ,x_{n}).

When $g$ is a simple constant $b$ , composition degenerates into a (partial) valuation, whose result is also known as restriction or co-factor.[18]

f|_{x_{i}=b}=f(x_{1},\ldots ,x_{i-1},b,x_{i+1},\ldots ,x_{n}).

In general, the composition of multivariate functions may involve several other functions as arguments, as in the definition of primitive recursive function. Given $f$ , a $n$ -ary function, and $n$ $m$ -ary functions $g 1, ..., g n$ , the composition of $f$ with $g 1, ..., g n$ , is the $m$ -ary function

h(x_{1},\ldots ,x_{m})=f(g_{1}(x_{1},\ldots ,x_{m}),\ldots ,g_{n}(x_{1},\ldots ,x_{m}))

.

This is sometimes called the generalized composite of f with $g 1, ..., g n$ .[19] The partial composition in only one argument mentioned previously can be instantiated from this more general scheme by setting all argument functions except one to be suitably chosen projection functions. Here $g 1, ..., g n$ can be seen as a single vector/tuple-valued function in this generalized scheme, in which case this is precisely the standard definition of function composition.[20]

A set of finitary operations on some base set X is called a clone if it contains all projections and is closed under generalized composition. Note that a clone generally contains operations of various arities.[19] The notion of commutation also finds an interesting generalization in the multivariate case; a function f of arity n is said to commute with a function g of arity m if f is a homomorphism preserving g, and vice versa i.e.:[19]

f(g(a_{11},\ldots ,a_{1m}),\ldots ,g(a_{n1},\ldots ,a_{nm}))=g(f(a_{11},\ldots ,a_{n1}),\ldots ,f(a_{1m},\ldots ,a_{nm}))

.

A unary operation always commutes with itself, but this is not necessarily the case for a binary (or higher arity) operation. A binary (or higher arity) operation that commutes with itself is called medial or entropic.[19]

Generalizations

Composition can be generalized to arbitrary binary relations. If $R \subseteq X \times Y$ and $S \subseteq Y \times Z$ are two binary relations, then their composition $R \circ S$ is the relation defined as ${(x, z) \in X \times Z : \exists y \in Y . (x, y) \in R \land (y, z) \in S}$ . Considering a function as a special case of a binary relation (namely functional relations), function composition satisfies the definition for relation composition. A small circle $R \circ S$ has been used for the infix notation of composition of relations, as well as functions. When used to represent composition of functions $(g\circ f)(x)\ =\ g(f(x))$ however, the text sequence is reversed to illustrate the different operation sequences accordingly.

The composition is defined in the same way for partial functions and Cayley's theorem has its analogue called the Wagner–Preston theorem.[21]

The category of sets with functions as morphisms is the prototypical category. The axioms of a category are in fact inspired from the properties (and also the definition) of function composition.[22] The structures given by composition are axiomatized and generalized in category theory with the concept of morphism as the category-theoretical replacement of functions. The reversed order of composition in the formula $(f \circ g) -1 = (g -1 \circ f -1)$ applies for composition of relations using converse relations, and thus in group theory. These structures form dagger categories.

Typography

The composition symbol $\circ$ is encoded as U+2218 ∘ RING OPERATOR (HTML ∘ · &compfn;, &SmallCircle;); see the Degree symbol article for similar-appearing Unicode characters. In TeX, it is written \circ.

gollark: Well, it might *cause* introversion™.

gollark: what

gollark: Ħ = ĸ

gollark: Ħ.

gollark: You do realise that friends are mostly a *good* thing, right?

Notes

Some authors use $f \circ g : X \to Z$ , defined by $(f \circ g)(x) = g (f (x))$ instead. This is common when a postfix notation is used, especially if functions are represented by exponents, as, for instance, in the study of group actions. See Dixon, John D.; Mortimer, Brian (1996). Permutation groups. Springer. p. 5. ISBN 0-387-94599-7.
The strict sense is used, e.g., in category theory, where a subset relation is modelled explicitly by an inclusion function.
Alfred Pringsheim's and Jules Molk's (1907) notation $n f (x)$ to denote function compositions must not be confused with Rudolf von Bitter Rucker's (1982) notation $n x$ , introduced by Hans Maurer (1901) and Reuben Louis Goodstein (1947) for tetration.

References

Velleman, Daniel J. (2006). How to Prove It: A Structured Approach. Cambridge University Press. p. 232. ISBN 978-1-139-45097-3.
Rodgers, Nancy (2000). Learning to Reason: An Introduction to Logic, Sets, and Relations. John Wiley & Sons. pp. 359–362. ISBN 978-0-471-37122-9.
Hollings, Christopher (2014). Mathematics across the Iron Curtain: A History of the Algebraic Theory of Semigroups. American Mathematical Society. p. 334. ISBN 978-1-4704-1493-1.
Grillet, Pierre A. (1995). Semigroups: An Introduction to the Structure Theory. CRC Press. p. 2. ISBN 978-0-8247-9662-4.
Dömösi, Pál; Nehaniv, Chrystopher L. (2005). Algebraic Theory of Automata Networks: An introduction. SIAM. p. 8. ISBN 978-0-89871-569-9.
Carter, Nathan (2009-04-09). Visual Group Theory. MAA. p. 95. ISBN 978-0-88385-757-1.
Ganyushkin, Olexandr; Mazorchuk, Volodymyr (2008). Classical Finite Transformation Semigroups: An Introduction. Springer Science & Business Media. p. 24. ISBN 978-1-84800-281-4.
Herschel, John Frederick William (1820). "Part III. Section I. Examples of the Direct Method of Differences". A Collection of Examples of the Applications of the Calculus of Finite Differences. Cambridge, UK: Printed by J. Smith, sold by J. Deighton & sons. pp. 1–13 [5–6]. Archived from the original on 2020-08-04. Retrieved 2020-08-04. (NB. Inhere, Herschel refers to his 1813 work and mentions Hans Heinrich Bürmann's older work.)
Cajori, Florian (1952) [March 1929]. "§472. The power of a logarithm / §473. Iterated logarithms / §533. John Herschel's notation for inverse functions / §535. Persistence of rival notations for inverse functions / §537. Powers of trigonometric functions". A History of Mathematical Notations. 2 (3rd corrected printing of 1929 issue, 2nd ed.). Chicago, USA: Open court publishing company. pp. 108, 176–179, 336, 346. ISBN 978-1-60206-714-1. ISBN 1-60206-714-7. Retrieved 2016-01-18. […] §473. Iterated logarithms […] We note here the symbolism used by Pringsheim and Molk in their joint Encyclopédie article: "²log_b a = log_b (log_b a), …, ^k+1log_b a = log_b (^klog_b a)."^[a] […] §533. John Herschel's notation for inverse functions, sin⁻¹ x, tan⁻¹ x, etc., was published by him in the Philosophical Transactions of London, for the year 1813. He says (p. 10): "This notation cos.⁻¹ e must not be understood to signify 1/cos. e, but what is usually written thus, arc (cos.=e)." He admits that some authors use cos.^m A for (cos. A)^m, but he justifies his own notation by pointing out that since d² x, Δ³ x, Σ² x mean dd x, ΔΔΔ x, ΣΣ x, we ought to write sin.² x for sin. sin. x, log.³ x for log. log. log. x. Just as we write d⁻ⁿ V=∫ⁿ V, we may write similarly sin.⁻¹ x=arc (sin.=x), log.⁻¹ x.=c^x. Some years later Herschel explained that in 1813 he used fⁿ(x), f⁻ⁿ(x), sin.⁻¹ x, etc., "as he then supposed for the first time. The work of a German Analyst, Burmann, has, however, within these few months come to his knowledge, in which the same is explained at a considerably earlier date. He[Burmann], however, does not seem to have noticed the convenience of applying this idea to the inverse functions tan⁻¹, etc., nor does he appear at all aware of the inverse calculus of functions to which it gives rise." Herschel adds, "The symmetry of this notation and above all the new and most extensive views it opens of the nature of analytical operations seem to authorize its universal adoption."^[b] […] §535. Persistence of rival notations for inverse function.— […] The use of Herschel's notation underwent a slight change in Benjamin Peirce's books, to remove the chief objection to them; Peirce wrote: "cos^[−1] x," "log^[−1] x."^[c] […] §537. Powers of trigonometric functions.—Three principal notations have been used to denote, say, the square of sin x, namely, (sin x)², sin x², sin² x. The prevailing notation at present is sin² x, though the first is least likely to be misinterpreted. In the case of sin² x two interpretations suggest themselves; first, sin x · sin x; second,^[d] sin (sin x). As functions of the last type do not ordinarily present themselves, the danger of misinterpretation is very much less than in case of log² x, where log x · log x and log (log x) are of frequent occurrence in analysis. […] The notation sinⁿ x for (sin x)ⁿ has been widely used and is now the prevailing one. […] (xviii+367+1 pages including 1 addenda page) (NB. ISBN and link for reprint of 2nd edition by Cosimo, Inc., New York, USA, 2013.)
Herschel, John Frederick William (1813) [1812-11-12]. "On a Remarkable Application of Cotes's Theorem". Philosophical Transactions of the Royal Society of London. London: Royal Society of London, printed by W. Bulmer and Co., Cleveland-Row, St. James's, sold by G. and W. Nicol, Pall-Mall. 103 (Part 1): 8–26 [10]. JSTOR 107384.
Peano, Giuseppe (1903). Formulaire mathématique (in French). IV. p. 229.
Peirce, Benjamin (1852). Curves, Functions and Forces. I (new ed.). Boston, USA. p. 203.
Pringsheim, Alfred; Molk, Jules (1907). Encyclopédie des sciences mathématiques pures et appliquées (in French). I. p. 195. Part I.
Ivanov, Oleg A. (2009-01-01). Making Mathematics Come to Life: A Guide for Teachers and Students. American Mathematical Society. pp. 217–. ISBN 978-0-8218-4808-1.
Gallier, Jean (2011). Discrete Mathematics. Springer. p. 118. ISBN 978-1-4419-8047-2.
Barr, Michael; Wells, Charles (1998). Category Theory for Computing Science (PDF). p. 6. Archived from the original (PDF) on 2016-03-04. Retrieved 2014-08-23. (NB. This is the updated and free version of book originally published by Prentice Hall in 1990 as ISBN 978-0-13-120486-7.)
ISO/IEC 13568:2002(E), p. 23
Bryant, R. E. (August 1986). "Logic Minimization Algorithms for VLSI Synthesis" (PDF). IEEE Transactions on Computers. C-35 (8): 677–691. doi:10.1109/tc.1986.1676819.
Bergman, Clifford (2011). Universal Algebra: Fundamentals and Selected Topics. CRC Press. pp. 79–80, 90–91. ISBN 978-1-4398-5129-6.
Tourlakis, George (2012). Theory of Computation. John Wiley & Sons. p. 100. ISBN 978-1-118-31533-0.
Lipscomb, S. (1997). Symmetric Inverse Semigroups. AMS Mathematical Surveys and Monographs. p. xv. ISBN 0-8218-0627-0.
Hilton, Peter; Wu, Yel-Chiang (1989). A Course in Modern Algebra. John Wiley & Sons. p. 65. ISBN 978-0-471-50405-4.

External links

"Composite function", Encyclopedia of Mathematics, EMS Press, 2001 [1994]
"Composition of Functions" by Bruce Atwood, the Wolfram Demonstrations Project, 2007.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[NB_Dixon_1996-1] Some authors use $f \circ g : X \to Z$ , defined by $(f \circ g)(x) = g (f (x))$ instead. This is common when a postfix notation is used, especially if functions are represented by exponents, as, for instance, in the study of group actions. See Dixon, John D.; Mortimer, Brian (1996). Permutation groups. Springer. p. 5. ISBN 0-387-94599-7.

[NB_Strict-3] The strict sense is used, e.g., in category theory, where a subset relation is modelled explicitly by an inclusion function.

[NB_Rucker-16] Alfred Pringsheim's and Jules Molk's (1907) notation $n f (x)$ to denote function compositions must not be confused with Rudolf von Bitter Rucker's (1982) notation $n x$ , introduced by Hans Maurer (1901) and Reuben Louis Goodstein (1947) for tetration.

[Velleman_2006-2] Velleman, Daniel J. (2006). How to Prove It: A Structured Approach. Cambridge University Press. p. 232. ISBN 978-1-139-45097-3.

[Rodgers_2000-4] Rodgers, Nancy (2000). Learning to Reason: An Introduction to Logic, Sets, and Relations. John Wiley & Sons. pp. 359–362. ISBN 978-0-471-37122-9.

[Hollings_2014-5] Hollings, Christopher (2014). Mathematics across the Iron Curtain: A History of the Algebraic Theory of Semigroups. American Mathematical Society. p. 334. ISBN 978-1-4704-1493-1.

[Grillet_1995-6] Grillet, Pierre A. (1995). Semigroups: An Introduction to the Structure Theory. CRC Press. p. 2. ISBN 978-0-8247-9662-4.

[Dömösi-Nehaniv_2005-7] Dömösi, Pál; Nehaniv, Chrystopher L. (2005). Algebraic Theory of Automata Networks: An introduction. SIAM. p. 8. ISBN 978-0-89871-569-9.

[Carter_2009-8] Carter, Nathan (2009-04-09). Visual Group Theory. MAA. p. 95. ISBN 978-0-88385-757-1.

[Ganyushkin-Mazorchuk_2008-9] Ganyushkin, Olexandr; Mazorchuk, Volodymyr (2008). Classical Finite Transformation Semigroups: An Introduction. Springer Science & Business Media. p. 24. ISBN 978-1-84800-281-4.

[Herschel_1820-10] Herschel, John Frederick William (1820). "Part III. Section I. Examples of the Direct Method of Differences". A Collection of Examples of the Applications of the Calculus of Finite Differences. Cambridge, UK: Printed by J. Smith, sold by J. Deighton & sons. pp. 1–13 [5–6]. Archived from the original on 2020-08-04. Retrieved 2020-08-04. (NB. Inhere, Herschel refers to his 1813 work and mentions Hans Heinrich Bürmann's older work.)

[Cajori_1929-11] Cajori, Florian (1952) [March 1929]. "§472. The power of a logarithm / §473. Iterated logarithms / §533. John Herschel's notation for inverse functions / §535. Persistence of rival notations for inverse functions / §537. Powers of trigonometric functions". A History of Mathematical Notations. 2 (3rd corrected printing of 1929 issue, 2nd ed.). Chicago, USA: Open court publishing company. pp. 108, 176–179, 336, 346. ISBN 978-1-60206-714-1. ISBN 1-60206-714-7. Retrieved 2016-01-18. […] §473. Iterated logarithms […] We note here the symbolism used by Pringsheim and Molk in their joint Encyclopédie article: "²log_b a = log_b (log_b a), …, ^k+1log_b a = log_b (^klog_b a)."^[a] […] §533. John Herschel's notation for inverse functions, sin⁻¹ x, tan⁻¹ x, etc., was published by him in the Philosophical Transactions of London, for the year 1813. He says (p. 10): "This notation cos.⁻¹ e must not be understood to signify 1/cos. e, but what is usually written thus, arc (cos.=e)." He admits that some authors use cos.^m A for (cos. A)^m, but he justifies his own notation by pointing out that since d² x, Δ³ x, Σ² x mean dd x, ΔΔΔ x, ΣΣ x, we ought to write sin.² x for sin. sin. x, log.³ x for log. log. log. x. Just as we write d⁻ⁿ V=∫ⁿ V, we may write similarly sin.⁻¹ x=arc (sin.=x), log.⁻¹ x.=c^x. Some years later Herschel explained that in 1813 he used fⁿ(x), f⁻ⁿ(x), sin.⁻¹ x, etc., "as he then supposed for the first time. The work of a German Analyst, Burmann, has, however, within these few months come to his knowledge, in which the same is explained at a considerably earlier date. He[Burmann], however, does not seem to have noticed the convenience of applying this idea to the inverse functions tan⁻¹, etc., nor does he appear at all aware of the inverse calculus of functions to which it gives rise." Herschel adds, "The symmetry of this notation and above all the new and most extensive views it opens of the nature of analytical operations seem to authorize its universal adoption."^[b] […] §535. Persistence of rival notations for inverse function.— […] The use of Herschel's notation underwent a slight change in Benjamin Peirce's books, to remove the chief objection to them; Peirce wrote: "cos^[−1] x," "log^[−1] x."^[c] […] §537. Powers of trigonometric functions.—Three principal notations have been used to denote, say, the square of sin x, namely, (sin x)², sin x², sin² x. The prevailing notation at present is sin² x, though the first is least likely to be misinterpreted. In the case of sin² x two interpretations suggest themselves; first, sin x · sin x; second,^[d] sin (sin x). As functions of the last type do not ordinarily present themselves, the danger of misinterpretation is very much less than in case of log² x, where log x · log x and log (log x) are of frequent occurrence in analysis. […] The notation sinⁿ x for (sin x)ⁿ has been widely used and is now the prevailing one. […] (xviii+367+1 pages including 1 addenda page) (NB. ISBN and link for reprint of 2nd edition by Cosimo, Inc., New York, USA, 2013.)

[Herschel_1813-12] Herschel, John Frederick William (1813) [1812-11-12]. "On a Remarkable Application of Cotes's Theorem". Philosophical Transactions of the Royal Society of London. London: Royal Society of London, printed by W. Bulmer and Co., Cleveland-Row, St. James's, sold by G. and W. Nicol, Pall-Mall. 103 (Part 1): 8–26 [10]. JSTOR 107384.

[Peano_1903-13] Peano, Giuseppe (1903). Formulaire mathématique (in French). IV. p. 229.

[Peirce_1852-14] Peirce, Benjamin (1852). Curves, Functions and Forces. I (new ed.). Boston, USA. p. 203.

[Pringsheim-Molk_1907-15] Pringsheim, Alfred; Molk, Jules (1907). Encyclopédie des sciences mathématiques pures et appliquées (in French). I. p. 195. Part I.

[Ivanov_2009-17] Ivanov, Oleg A. (2009-01-01). Making Mathematics Come to Life: A Guide for Teachers and Students. American Mathematical Society. pp. 217–. ISBN 978-0-8218-4808-1.

[Gallier_2011-18] Gallier, Jean (2011). Discrete Mathematics. Springer. p. 118. ISBN 978-1-4419-8047-2.

[Barr-Wells_1990-19] Barr, Michael; Wells, Charles (1998). Category Theory for Computing Science (PDF). p. 6. Archived from the original (PDF) on 2016-03-04. Retrieved 2014-08-23. (NB. This is the updated and free version of book originally published by Prentice Hall in 1990 as ISBN 978-0-13-120486-7.)

[ISOIEC13568-20] ISO/IEC 13568:2002(E), p. 23

[Bryant_1986-21] Bryant, R. E. (August 1986). "Logic Minimization Algorithms for VLSI Synthesis" (PDF). IEEE Transactions on Computers. C-35 (8): 677–691. doi:10.1109/tc.1986.1676819.

[Bergman_2011-22] Bergman, Clifford (2011). Universal Algebra: Fundamentals and Selected Topics. CRC Press. pp. 79–80, 90–91. ISBN 978-1-4398-5129-6.

[Tourlakis_2012-23] Tourlakis, George (2012). Theory of Computation. John Wiley & Sons. p. 100. ISBN 978-1-118-31533-0.

[Lipcomb_1997-24] Lipscomb, S. (1997). Symmetric Inverse Semigroups. AMS Mathematical Surveys and Monographs. p. xv. ISBN 0-8218-0627-0.

[Hilton-Wu_1989-25] Hilton, Peter; Wu, Yel-Chiang (1989). A Course in Modern Algebra. John Wiley & Sons. p. 65. ISBN 978-0-471-50405-4.