For one AES is built for three key sizes 128, 192 or 256 bits.
Currently, brute-forcing 128 bits is not even close to feasible. Hypothetically, if an AES Key had 129 bits, it would take twice as long to brute-force a 129 bit key than a 128 bit key. This means larger keys of 192 bits and 256 bits would take much much much longer to attack. It would take so incredibly long to brute-force one of these keys that the sun would stop burning before the key was realized.
2^256=115792089237316195423570985008687907853269984665640564039457584007913129639936
That's a big freaking number. That's how many possibly keys there are. Assuming the key is random, if you divide that by 2 then you have how many keys it will take on average to brute-force AES-256
In a sense we do have the really big cipher keys you are talking of. The whole point of a symmetric key is to make it unfeasible to brute-force. In the future, if attacking a 256bit key becomes possible then keysizes will surely increase, but that is quite a ways down the road.
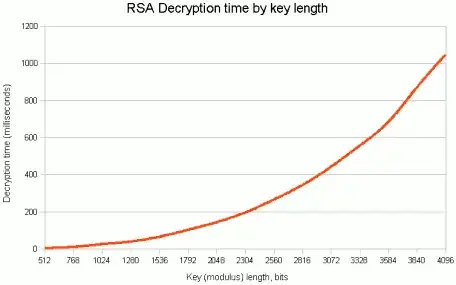
The reason RSA keys are much larger than AES keys is because they are two completely different types of encryption. This means a person would not attack a RSA key the same as they would attack an AES Key.
Attacking symmetric keys is easy.
- Start with a bitstring
000...
- Decrypt ciphertext with that bitstring.
- If you can read it, you succeeded.
- If you cannot read it then increment the bitstring
Attacking an RSA key is different...because RSA encryption/decryption works with big semi-prime numbers...the process is mathy. With RSA, you don't have to try every possible bit string. You try far fewer than 2^1024 or 2^2048 bitstrings...but it's still not possible to bruteforce. This is why RSA and AES keys differ in size.[1]
To sum up everything and answer your question in 1 sentence. We don't need ridiculously big symmetric keys because we already have ridiculously big symmetric keys. 256 bit encryption sounds wimpy compared to something like a 2048 bit RSA Key, but the algorithms are different and can't really be compared 'bit to bit' like that. In the future if there is a need to longer keys then there will be new algorithms developed to handle larger keys. And if we ever wanted to go bigger on current hardware, it's simply a time tradeoff. Bigger key means longer decryption time means slower communication. This is especially important for a cipher since your internet browser will establish and then use a symmetric key to send information.