Thanks to FryAmTheEggman for some necessary inspiration for the XOR solution.
0000 !@
0001 ?.|@!
0010 #?#!)@
0011 ?!@
0100 +?|@!?
0101 ??!@
0110 ?<@!!<_\~(
0111 ?<<@!
1000 )\!#?@{
1001 (~?/@#!
1010 ??|@!)
1011 \#??!1@
1100 ?(~!@
1101 ?.|@!)
1110 ?$@#)!<
1111 1!@
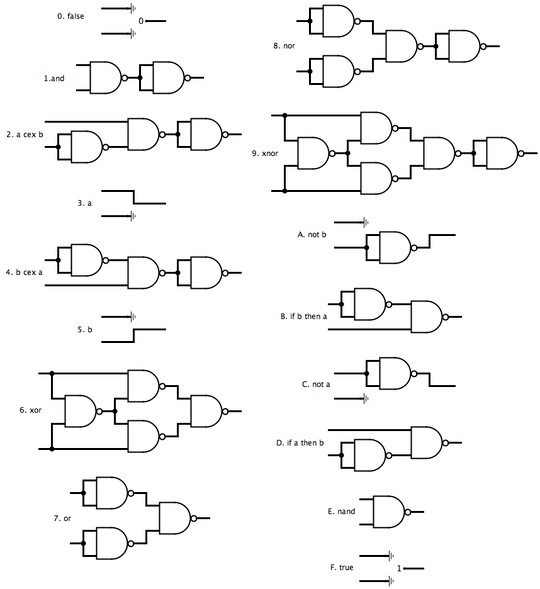
All programs use 0 for false and 1 for true.
Try it online! This is not a test suite, you'll have to copy in the different programs and inputs yourself.
The above solution is within 2-bytes of optimality (unless we relax the truthy/falsy interpretation, I guess). I've let a brute force search run for close to two days over all programs that fit into side-length 2, i.e. up to 7 bytes (not quite all programs - I made a few assumptions on what every valid program needs and what no valid program could have). The search found solutions for 15 of the 16 possible gates - and often a lot more than just one. You can find a list of all the alternative solutions in this pastebin where I've also grouped them by equivalent behaviour. The ones I'm showing above I've selected because they are either the simplest or the most interesting solution, and I'll add explanations for them tomorrow.
As for the 16th gate: XOR is the only gate that can apparently not be implemented in 7 bytes. A brute force search over larger programs is unfortunately not feasible with the code I currently have. So XOR had to be written by hand. The shortest I've found so far is the above 10-byte program, which is based on a failed (but very close) attempt by FryAmTheEggman. It's possible that an 8-byte or 9-byte solution exists, but other than that, all the solutions should indeed be optimal.
Explanations
Warning: wall of text. On the off-chance anyone's interested how these highly compressed Hexagony programs actually work, I've included explanations for each of them below. I've tried to choose the simplest solution for each gate in cases where more than one optimal program exists, in order to keep the explanations reasonably short. However, some of them still boggle the mind, so I thought they deserve a bit more elaboration.
0000: False
I don't think we'll need a diagram for this one:
! @
. . .
. .
Since the entire memory grid is initialised to zeros, ! simply prints a zero and @ terminates the program.
This is also the only 2-byte solution.
0001: And
? .
| @ !
. .
This basically implements short-circuiting. The grey diagram below shows the beginning of the program, where the first input is read with ? and the instruction pointer (IP) wraps around to the the left corner where the | mirror reflects it. Now the corner acts as a conditional, such there are two different execution paths depending on the value of the first input. The red diagram shows the control flow for A = 0 and the green diagram for A = 1:



As you can see, when the A is 0, then we simply print it and terminate (remember that all . are no-ops). But when A is 1, then the IP traverses the first row again, reading B and printing that instead.
In total there are sixteen 5-byte solutions for this gate. Fourteen of those are essentially the same as the above, either using > instead of | or replacing the . with a command that's effectively a no-op, or putting ? in the second position:
?.|@! .?|@! ?=|@! =?|@! ?_|@! _?|@! ?0|@!
?.>@! .?>@! ?=>@! =?>@! ?_>@! _?>@! ?0>@!
And then there are two other solutions (which are equivalent to each other). These also implement the same short-circuiting logic, but the execution paths are a bit crazier (and left as an exercise to the reader):
?<!@|
?<!@<
0010: A and not B
# ?
# ! )
@ .
This also implements a form of short-circuiting, but due to the use of # the control flow is much trickier. # is a conditional IP switch. Hexagony actually comes with six IPs labelled 0 to 5, which start in the six corners of the grid, pointing along their clockwise edge (and the program always begins with IP 0). When a # is encountered, the current value is taken modulo 6, and control flow continues with the corresponding IP. I'm not sure what fit of madness made me add this feature, but it certainly allows for some surprising programs (like this one).
We will distinguish three cases. When A = 0, the program is fairly simple, because the value is always 0 when # is encountered such that no IP-switching takes place:
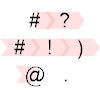
# does nothing, ? reads A (i.e. also does nothing), # still does nothing, ! prints the 0, ) increments it (this is important, otherwise the IP would not jump to the third line), @ terminates the program. Simple enough. Now let's consider the case (A, B) = (1, 0):
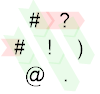
The red path still corresponds to IP 0, and I've added the green path for IP 1. We see that after ? reads A (1 this time), the # switches to the IP that starts in the top right corner. That means ? can read B (0). Now ) increments that to 1, such that the # in the top left corner does nothing and we remain with IP 1. The ! prints the 1 and the IP wraps around the left diagonal. # still does nothing and @ terminates the program.
Finally, the really weird case where both inputs are 1:
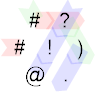
This time, the second input is also 1 and ) increments it to 2. That means the # in the top left corner causes another IP switch to IP 2, indicate in blue. On that path, we first increment it further to 3 (although that's irrelevant) and then pass the ? a third time. Since we've now hit EOF (i.e. the input is exhausted), ? returns 0, ! prints that, and @ terminates the program.
Notably, this is the only 6-byte solution for this gate.
0011: A
? !
@ . .
. .
This is simple enough that we won't need a diagram: ? reads A, ! prints it, @ terminates.
This is the only 3-byte solution for this gate. (In principle, it would also be possible to do ,;@, but the search didn't include ;, because I don't think it can ever save bytes over ! for this task.)
0100: B and not A
+ ?
| @ !
? .
This one is a lot simpler than its "brother" 0010. The control flow is actually the same as we've seen above for 0001 (And). If A = 0, then the IP traverses the lower line, reading B and printing that before terminating. If A = 1 then the IP traverses the first line again, also reading B, but the + adds two unused memory edges so all it does is reset the current value to 0, so that ! always prints 0.
There are quite a lot of 6-byte alternatives to this (42 in total). First, there's a ton of solutions equivalent to the above. We can again choose freely between | and >, and + can be replaced with any other command that gives us an empty edge:
"?|@!? &?|@!? '?|@!? *?|@!? +?|@!? -?|@!? ^?|@!? {?|@!? }?|@!?
"?>@!? &?>@!? '?>@!? *?>@!? +?>@!? -?>@!? ^?>@!? {?>@!? }?>@!?
In addition, we can also use ] instead of ?. ] moves to the next IP (i.e. selects IP 1), so that this branch instead reuses the ? in the top right corner. That gives another 18 solutions:
"?|@!] &?|@!] '?|@!] *?|@!] +?|@!] -?|@!] ^?|@!] {?|@!] }?|@!]
"?>@!] &?>@!] '?>@!] *?>@!] +?>@!] -?>@!] ^?>@!] {?>@!] }?>@!]
And then there's six other solutions that all work differently with varying levels of craziness:
/[<@!? ?(#!@] ?(#>@! ?/@#/! [<<@!? [@$\!?
0101: B
? ?
! @ .
. .
Woohoo, another simple one: read A, read B, print B, terminate. There are actually alternatives to this though. Since A is only a single character, we can also read it with ,:
,?!@
And there's also the option of using a single ? and using a mirror to run through it twice:
?|@! ?>@!
0110: Xor
? < @
! ! < _
\ ~ ( . .
. . . .
. . .
Like I said above, this was the only gate that wouldn't fit in side-length 2, so this a handwritten solution by FryAmTheEggman and myself, and there's a good chance that it isn't optimal. There are two cases to distinguish. If A = 0 the control flow is fairly simple (because in that case we only need to print B):
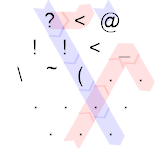
We start on the red path. ? reads A, < is a branch which deflects the zero left. The IP wraps to the bottom, then _ is another mirror, and when the IP hits the corner, it wraps to the top left corner and continues on the blue path. ? reads B, ! prints it. Now ( decrements it. This is important because it ensures that the value is non-positive (it's either 0 or -1 now). That makes IP wrap to the to right corner, where @ terminates the program.
When A = 1 things get a bit trickier. In that case we want to print not B, which in itself isn't too difficult, but the execution path is a bit trippy.
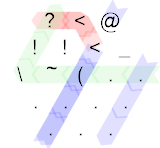
This time, the < deflects the IP right and then next < just acts as a mirror. So the IP traverses the same path in reverse, reading B when it encounters ? again. The IP wraps around to the right corner and continues on the green path. It next encounters (~ which is "decrement, multiply by -1", which swaps 0 and 1 and therefore computes not B. \ is just a mirror and ! prints the desired result. Then ? tries to return another number but returns zero. The IP now continues in the bottom left corner on the blue path. ( decrements, < reflects, ( decrements again, so that the current value is negative when the IP hits the corner. It moves across the bottom right diagonal and then finally hits @ to terminate the program.
0111: Or
? <
< @ !
. .
More short-circuiting.


The A = 0 case (the red path) is a bit confusing here. The IP gets deflected left, wraps to the bottom left corner, gets immediately reflected by the < and returns to the ? to read B. It then wraps to the rigt corner, prints B with ! and terminates.
The A = 1 case (the green path) is a bit simpler. The < branch deflects the IP right, so we simply print the !, wrap back to the top left, and terminate at @.
There is only one other 5-byte solution:
\>?@!
It works essentially the same, but the actual execution paths are quite different and it uses a corner for branching instead of a <.
1000: Nor
) \
! # ?
@ {
This might be my favourite program found in this search. The coolest thing is that this implementation of nor actually works for up to 5 inputs. I'll have to get into the details of the memory model a bit to explain this one. So as a quick refresher, Hexagony's memory model is a separate hexagonal grid, where each edge holds an integer value (initially all zero). There's a memory pointer (MP) which indicates an edge and a direction along that edge (such that there's two neighboring edges in front of and behind the current edge, with meaningful left and right neighbours). Here is a diagram of the edges we'll be using, with the MP starting out as shown in red:
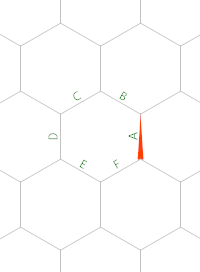
Let's first consider the case where both inputs are 0:

We start on the grey path, which simply increments edge A to 1 so that the # switches to IP 1 which is the blue path, starting in the top right corner. \ does nothing there and ? reads an input. We wrap to the top left corner where ) increments that input. Now as long as the input is zero, this will result in a 1, so that # doesn't do anything. Then { moves the MP to the left, i.e. on the first iteration from A to B. Since this edge still has its initial zero the IP wraps back to the top right corner and on a new memory edge. So this loop will continue as long as ? reads zeros, moving the MP around the hexagon from B to C to D and so on. It doesn't matter whether ? returns a zero because it was an input or because it was EOF.
After six iterations through this loop, { returns to A. This time, the edge already holds the value 1 from the very first iteration, so the IP wraps to the left corner and continues on the green path instead. ! simply prints that 1 and @ terminates the program.
Now what if any of the inputs is 1?
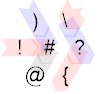
Then ? reads that 1 at some point and ) increments it to 2. That means # will now switch IPs again and we'll continue in the right corner on the red path. ? reads another input (if there is one), which doesn't really matter and { moves one edge further. This has to be an unused edge, hence this works for up to 5 inputs. The IP wraps to the top right where it's immediately reflected and wraps to the left corner. ! prints the 0 on the unused edge and # switches back to IP 0. That IP was still waiting around on the #, going southwest (grey path), so it immediately hits the @ and terminates the program.
In total there are seven 7-byte solutions for this gate. 5 of them work the same as this and simply use other commands to move to an unused edge (and may walk around a different hexagon or in a different direction):
)\!#?@" )\!#?@' )\!#?@^ )\!#?@{ )\!#?@}
And there is one other class of solutions which only works with two inputs, but whose execution paths are actually even messier:
?]!|<)@ ?]!|<1@
1001: Equality
( ~
? / @
# !
This also makes very clever use of conditional IP selection. We need to distinguish again between A = 0 and A = 1. In the first case we want to print not B, in the second we want to print B. For A = 0 we also distinguish the two cases for B. Let's start with A = B = 0:
We start on the grey path. (~ can be ignored, the IP wraps to the left corner (still on the grey path) and reads A with ?. ( decrements that, so we get -1 and IP wrap to the bottom left corner. Now like I said earlier, # takes the value modulo 6 before choosing he IP, so a value of -1 actually gets out IP 5, which starts in the left corner on the red path. ? reads B, ( decrements that as well so that we remain on IP 5 when we hit # again. ~ negates the -1 so that the IP wraps to the bottom right corner, prints the 1 and terminates.
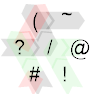
Now if B is 1 instead, the current value will be 0 when we hit # the second time, so we switch back to IP 0 (now on the green path). That hits ? a third time, yielding 0, ! prints it and @ terminates.

Finally, the case where A = 1. This time the current value is already zero when we hit # for the first time, so this never switches to IP 5 in the first place. We simply continue immediately on the green path. ? now doesn't just give a zero but returns B instead. ! prints it and @ terminates again.
In total there are three 7-byte solutions for this gate. The other two work very differently (even from each other), and make even weirder use of #. In particular they read one or more values with , (reading a character code instead of an integer) and then use that value modulo 6 to pick an IP. It's pretty nuts.
),)#?@!
?~#,~!@
1010: Not B
? ?
| @ !
) .
This one is fairly simple. The execution path is the horizontal branch we already know from and earlier. ?? reads A and then immediately B. After reflecting at | and branching, for B = 0 we will execute the bottom branch, where ) increments the value to 1 which is then printed by !. On the top branch (if B = 1) the ? simply reset the edge to 0 which is then also printed by !.
There are eight 6-byte programs for this gate. Four of them are pretty much the same, using either > instead of | or 1 instead of ) (or both):
??>@!) ??>@!1 ??|@!) ??|@!1
Two use a single ? which is used twice due to a mirror. The negation then happens as we did for xor with either (~ or ~).
?>!)~@ ?>!~(@
And finally, two solutions use a conditional IP switch, because why use the simple way if the convoluted one also works:
??#)!@ ??#1!@
1011: B implies A
\ #
? ? !
1 @
This uses some rather elaborate IP switching. I'll start with the A = 1 case this time, because it's simpler:
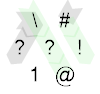
We start on the grey path, which reads A with ? and then hits the #. Since A is 1 this switches to IP 1 (green path). The ! immediately prints that, the IP wraps to the top left, reads B (unnecessarily) and terminates.
When A = 0 things get a bit more interesting. First let's consider A = B = 0:
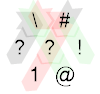
This time, the # does nothing and we remain on IP 0 (red path from that point onward). ? reads B and 1 turns it into a 1. After wrapping to the top left corner, we hit # again, so we end up on the green path after all, and print 1 as before, before terminating.
Finally, here is (A, B) = (0, 1), the false case:

Note that I've removed the initial grey path for clarity, but the program begins the same way, and we end up on the red path as before. So this time the second ? returns 1. Now we encounter the 1. At this point it's important to understand what digits actually do in Hexagony (so far we've only used them on zeros): when a digit is encountered, the current value is multiplied by 10 and then the digit is added. This is normally used to write decimal numbers verbatim into the source code, but it means that B = 1 is actually mapped to the value 11. So when we hit #, this is taken modulo 6 to give 5 and hence we switch to IP 5 (instead of 1 as before) and continue on the blue path. Hitting ? a third time returns a zero, so ! prints that, and after another two ?, the IP wraps to the bottom right where the program terminates.
There are four 7-byte solutions to this and they all work differently:
#)/!?@$ <!?_@#1 \#??!1@ |/)#?@!
1100: Not A
? (
~ ! @
. .
Just a simple linear one: read A with ?, negate with (~, print with !, terminate with @.
There's one alternative solution, and that's negating with ~) instead:
?~)!@
1101: A implies B
? .
| @ !
) .
This is a lot simpler than the opposite implication we just talked about. It's again one of those horizontal branch programs, like the one for and. If A is 0, it simply gets incremented to 1 on the bottom branch and printed. Otherwise, the top branch is executed again where ? reads B and then ! prints that instead.
There's a ton of alternatives here (66 solutions in total), mostly due to free choice of effective no-ops. For a start we can vary the above solution in all the same ways we could for and and we can also choose between ) and 1:
?.|@!) .?|@!) ?=|@!) =?|@!) ?_|@!) _?|@!) ?0|@!)
?.|@!1 .?|@!1 ?=|@!1 =?|@!1 ?_|@!1 _?|@!1 ?0|@!1
?.>@!) .?>@!) ?=>@!) =?>@!) ?_>@!) _?>@!) ?0>@!)
?.>@!1 .?>@!1 ?=>@!1 =?>@!1 ?_>@!1 _?>@!1 ?0>@!1
And then there's a different version using conditional IP selection, where the first command can be chosen almost arbitrarily, and there is also a choice between ) and 1 for some of those options:
"?#1!@ &?#1!@ '?#1!@ )?#1!@ *?#1!@ +?#1!@ -?#1!@ .?#1!@
0?#1!@ 1?#1!@ 2?#1!@ 3?#1!@ 4?#1!@ 5?#1!@ 6?#1!@ 7?#1!@
8?#1!@ 9?#1!@ =?#1!@ ^?#1!@ _?#1!@ {?#1!@ }?#1!@
"?#)!@ &?#)!@ '?#)!@ *?#)!@ +?#)!@ -?#)!@
0?#)!@ 2?#)!@ 4?#)!@ 6?#)!@
8?#)!@ ^?#)!@ _?#)!@ {?#)!@ }?#)!@
1110: Nand
? $
@ # )
! <
The last complicated one. If you're still reading, you've almost made it. :) Let's look at A = 0 first:

? reads A and then we hit $. This is a jump command (like Befunge's #) which skips the next instruction so that we don't terminate on the @. Instead the IP continues at #. However since A is 0, this doesn't do anything. ) increments it to 1 so that the IP continues on the bottom path where the 1 is printed. The < deflects the IP to the right where it wraps to the left corner and the program terminates.
Next, when the input is (A, B) = (1, 0) we get this situation:
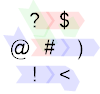
It's essentially the same as before except that at the # we switch to IP 1 (green path), but since B is 0 we switch back to IP 0 when we hit # a second time (now blue path), where it prints 1 as before.
Finally, the A = B = 1 case:
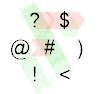
This time, when we # the second time, the current value is still 1 so that we don't change the IP again. The < reflects it and the third time we hit ? we get a zero. Hence the IP wraps to the bottom left where ! prints the zero and the program ends.
There are nine 7-byte solutions in total for this. The first alternative simply uses 1 instead of ):
?$@#1!<
Then there's two solutions that will do your head in with the amount of IP switching that's going on:
)?#_[!@ 1?#_[!@
These actually blew my mind: the interesting part is that IP switching can be used as a deferred conditional. The language's IP-switching rules are such that the current IP makes another step before the switch happens. If that step happens to go through a corner, then the current value decides on which branch the IP will continue if we ever switch back to it. Exactly this happens when the input is A = B = 1. Although this is all consistent with how I designed the language, I was never aware of this implication of the spec, so it's nice when my language teaches me some new tricks :D.
Then there's a third solution whose amount of IP switching is even worse (although it doesn't make use of that deferred conditional effect):
>?1]#!@
And then there's another one:
?$@#)!<
And then there's these four equivalent solutions, which do use some non-conditional IP switching and instead implement all the logic via branches and corners:
]<?<@!) ]<?<@!1 ]|?<@!) ]|?<@!1
1111: True
1 !
@ . .
. .
You've earned yourself something simple for the end: set edge to 1, print with !, terminate with @. :)
Of course, there's one alternative:
)!@
As usual, all control flow diagrams created with Timwi's HexagonyColorer and the memory diagram with his EsotericIDE.



















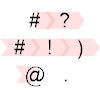
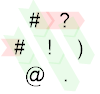





























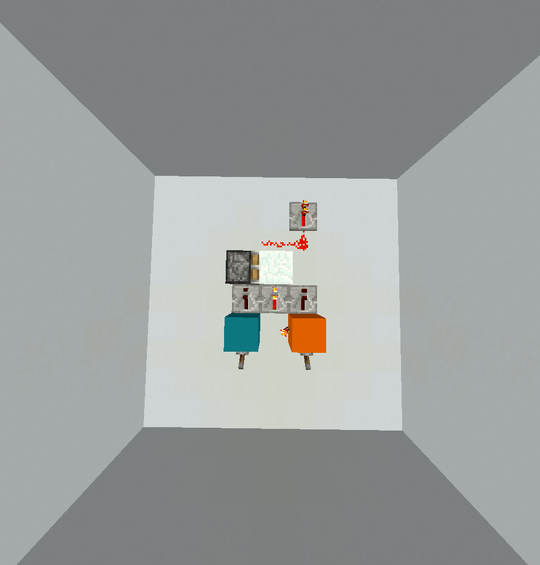








2Your functions/programs may share code. What does this mean? Also, may the programs be in different languages? – Lynn – 2016-06-14T23:36:04.563
You should probably specify that all programs should use a consistent input order – Luis Mendo – 2016-06-14T23:48:11.037
2I find the explanation confusing: "of the 4 possible inputs each can have and output of truthy and falsy". Doesn't this imply 8 (4*2) states? – DavidC – 2016-06-14T23:50:03.447
4The names you're missing are the AND-NOT gates (A AND NOT B and B AND NOT A). – Mego – 2016-06-15T01:33:45.133
2Do the function have to coexist or can I name all of them
f? – Dennis – 2016-06-15T02:39:32.3572
Related topic: http://codegolf.stackexchange.com/questions/12103/generate-a-universal-binary-function-lookup-table
– luser droog – 2016-06-15T03:00:21.2171@DavidC For each input combination you can make an independent choice between true and false for the output. That's 222*2 = 2^4 = 16 combinations. – Martin Ender – 2016-06-15T07:25:39.647
14So it happened again. There are 18 answer, mostly simple and correct, then out of nowhere the question became "unclear what you're asking". I you don't like a challenge, go on, take another, do not close it! – edc65 – 2016-06-15T17:25:04.260
Why do 12 and 14 return a truthy value when
BandAare respectively falsey? – user8397947 – 2016-06-15T20:08:50.5074
@dorukayhan See: vacuous truth
– Sp3000 – 2016-06-15T21:19:02.8001Do the truthy values I use for the programs have to be the same for all inputs/outputs, or can truthy mean "anything but zero"? And if an output can be something, does that have to be an acceptable input (can I assume inputs are always
0and1, but outputs can be0and anything else for truthy). – mbomb007 – 2016-06-16T18:48:56.157@mbomb007 It depends on the language. As long as they are valid truthy and falsey results, they don't have to be consistent. – Leaky Nun – 2016-06-16T18:51:33.520
@LeakyNun But can I require the inputs to be consistent, always
0or-1, and the outputs can be any truthy/falsy values that the language accepts for an IF statement? – mbomb007 – 2016-06-16T19:01:58.433Yes, that is correct. – Leaky Nun – 2016-06-16T19:10:33.460
2So just a note on the questions — you're not really golfing the logic gates so much as you are golfing all 16 logical operators. – Joe Z. – 2016-06-22T03:41:57.697
@LeakyNun do you permit the use of different languages within one submission? – Rohan Jhunjhunwala – 2016-07-29T21:43:42.433
1Does our program/function have to be able to accept anything that's truthy/falsy, or can we restrict its input (e.g. to only strings and numbers, or to only 0 or 1)? – msh210 – 2016-08-01T19:50:01.067
@LeakyNun You're asking for a 15 byte answer, when the golf requires 16 programs. Seriously? – None – 2016-08-04T17:09:03.607
@tuskiomi One program can be empty. – Leaky Nun – 2016-08-04T17:10:01.350
@LeakyNun is that a permission, or a hint? – None – 2016-08-04T17:10:31.900
@tuskiomi You don't need my permission to submit an empty program as one of the programs. Jelly already does this.
– Leaky Nun – 2016-08-04T17:11:37.507@LeakyNun alright, I was curious if you were letting us skip one of the gates, or if it was possible. – None – 2016-08-04T17:13:08.523
What does
A implies Band vice versa mean? – caird coinheringaahing – 2017-11-17T23:29:01.707A implies B is a logic gate that gives you false if and only if A is true and B is false. – Leaky Nun – 2017-11-17T23:31:35.573
Does the program need to terminate? Or can it print the result and hang? – FlipTack – 2017-11-18T19:24:51.083
@FlipTack I think there's a meta consensus deciding that programs need to terminate. Sorry for the late response! – MilkyWay90 – 2019-05-04T20:01:01.430