8
1
A 2-way universal logic processor (2ULP) is a network of logic gates that takes two input wires A and B, as well as four other inputs L_, L_a, L_b, and L_ab, and produces a single output L(a, b) using the four L inputs as a truth table function:
- The 2ULP returns
L_ifAandBare both0. - It returns
L_aifA = 1andB = 0. - It returns
L_bifA = 0andB = 1. - It returns
L_abifAandBare both1.
For example, given the inputs L_ = 0, L_a = 1, L_b = 1, and L_ab = 0, then the output L(a, b) will be equal to A xor B.
Your task is to build a 2ULP using only NAND gates, using as few NAND gates as possible. To simplify things, you may use AND, OR, NOT, and XOR gates in your diagram, with the following corresponding scores:
NOT: 1AND: 2OR: 3XOR: 4
Each of these scores corresponds to the number of NAND gates that it takes to construct the corresponding gate.
The logic circuit that uses the fewest NAND gates to produce a correct construction wins.
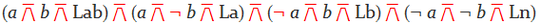
1My digital logic design skills are so rusty it's laughable, but I greatly enjoy the end results of these competitions. +1 – ProgrammerDan – 2014-03-28T16:23:57.320
With two-input NAND gates, there's not much room for creativity in this design. Perhaps, rather than requiring that the device take six inputs, design a block with has an arbitrary number of inputs and one output, and require that given two inputs A and B and a choice of one of the sixteen functions, it must be possible to connect the block's inputs to some combination of A, B, High, and Low, such that the output will yield that function. Such a device would be a universal 2-way logic processor (just add wires), but could probably be done in a lot less than 11 gates. – supercat – 2014-03-28T18:56:43.477
1We should invent [tag:gate-golf], where you write in the smallest amount of gates. – TheDoctor – 2014-03-29T13:53:57.300
That's what [tag:atomic-code-golf] + [tag:logic-gates] is for. – Joe Z. – 2014-03-29T15:03:12.003