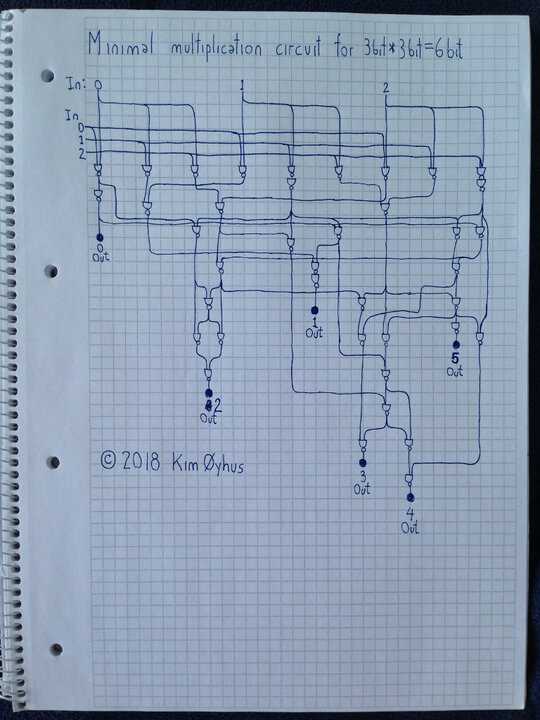
39 gates
I am quite sure there are no simpler designs than mine here.
It was very difficult to make. I make other minimal circuits too.
Transmission delay is indicated by downward position of each NAND gate on the sheet.
Verilog code and testing:
// MINIMAL 3 BIT MULTIPLICATOR
//
// The simplest 3 bit multiplicator possible, using 39 NAND gates only.
//
// I have also made multiplicators that are faster, more efficient,
// use different gates, and multiply bigger numbers. And I also do
// hard optimization of other circuits. You may contact me at
// kim.oyhus@gmail.com
//
// This is my entry to win this hard Programming Puzzle & Code Golf
// at Stack Exchange:
// https://codegolf.stackexchange.com/questions/12261/build-a-multiplying-machine-using-nand-logic-gates/
//
// By Kim Øyhus 2018 (c) into (CC BY-SA 3.0)
// This work is licensed under the Creative Commons Attribution 3.0
// Unported License. To view a copy of this license, visit
// https://creativecommons.org/licenses/by-sa/3.0/
module mul3x3 ( in_000, in_001, in_002, in_003, in_004, in_005, out000, out001, out002, out003, out004, out005 );
input in_000, in_001, in_002, in_003, in_004, in_005;
output out000, out001, out002, out003, out004, out005;
wire wir000, wir001, wir002, wir003, wir004, wir005, wir006, wir007, wir008, wir009, wir010, wir011, wir012, wir013, wir014, wir015, wir016, wir017, wir018, wir019, wir020, wir021, wir022, wir023, wir024, wir025, wir026, wir027, wir028, wir029, wir030, wir031, wir032;
nand gate000 ( wir000, in_000, in_005 );
nand gate001 ( wir001, in_000, in_004 );
nand gate002 ( wir002, in_000, in_003 );
nand gate003 ( out000, wir002, wir002 );
nand gate004 ( wir003, in_004, in_001 );
nand gate005 ( wir004, wir003, wir003 );
nand gate006 ( wir005, in_003, in_002 );
nand gate007 ( wir006, wir000, wir005 );
nand gate008 ( wir007, in_004, in_002 );
nand gate009 ( wir008, in_001, in_005 );
nand gate010 ( wir009, wir008, wir007 );
nand gate011 ( wir010, in_001, in_003 );
nand gate012 ( wir011, wir001, wir010 );
nand gate013 ( wir012, out000, wir004 );
nand gate014 ( wir013, wir004, wir012 );
nand gate015 ( wir014, wir011, wir012 );
nand gate016 ( out001, wir014, wir014 );
nand gate017 ( wir015, in_002, in_005 );
nand gate018 ( wir016, wir015, wir015 );
nand gate019 ( wir017, out000, wir016 );
nand gate020 ( wir018, wir017, wir013 );
nand gate021 ( wir019, wir016, wir018 );
nand gate022 ( wir020, wir019, wir009 );
nand gate023 ( wir021, wir020, wir017 );
nand gate024 ( wir022, wir020, wir009 );
nand gate025 ( wir023, wir022, wir021 );
nand gate026 ( out005, wir022, wir022 );
nand gate027 ( wir024, wir016, wir022 );
nand gate028 ( wir025, wir006, wir018 );
nand gate029 ( wir026, wir025, wir006 );
nand gate030 ( wir027, wir025, wir018 );
nand gate031 ( out002, wir026, wir027 );
nand gate032 ( wir028, wir004, wir027 );
nand gate033 ( wir029, wir023, wir028 );
nand gate034 ( wir030, wir028, wir028 );
nand gate035 ( wir031, wir030, wir021 );
nand gate036 ( out004, wir031, wir024 );
nand gate037 ( wir032, wir029, wir031 );
nand gate038 ( out003, wir032, wir032 );
endmodule
module mul3x3_test;
reg [5:0] AB; // C=A*B
wire [5:0] C;
mul3x3 U1 (
.in_000 (AB[0]),
.in_001 (AB[1]),
.in_002 (AB[2]),
.in_003 (AB[3]),
.in_004 (AB[4]),
.in_005 (AB[5]),
.out000 (C[0]),
.out001 (C[1]),
.out002 (C[2]),
.out003 (C[3]),
.out004 (C[4]),
.out005 (C[5])
);
initial AB=0;
always #10 AB = AB+1;
initial begin
$display("\t\ttime,\tA,\tB,\tC");
$monitor("%d,\t%b\t%b\t%b",$time, AB[5:3], AB[2:0],C);
end
initial #630 $finish;
endmodule
// iverilog -o mul3x3_test mul3x3_test.v
// vvp mul3x3_test
Kim Øyhus

Just to explain the bump: Someone posted here as an answer a claim that he has a 39-gate solution available. He didn't post the solution, but I'm still curious if 39 gates is actually possible. – John Dvorak – 2016-05-17T07:54:29.997
I'm trying to make a last-place example in Logisim. This stuff is hard. – Joe Z. – 2013-08-08T06:22:08.217
I got enough of this stuff in my school, no thanks. – Johannes Kuhn – 2013-08-08T08:02:56.777
7I have a universal optimizer for tasks like this. It provably finds the shortest program to compute a k-output boolean function. If I gave it a week, it could tell me if the 13 gate 2x2 multiplier it found is optimal. 3x3? I'll be dead before it finishes. – boothby – 2013-08-09T04:14:58.557
1That 13 gate 2x2 multiplier is optimal (and contained in Jan's answer). With that, and another few pieces I can optimize, I very strongly suspect 60 to be optimal for this problem. I really hope somebody proves me wrong. – boothby – 2013-08-10T05:49:34.250
@boothby Not really. Naive application of adder trees leads to an 18-gate solution (4 ANDs, 2 half-adders), which leads me to an idea: I should be able to steal^k^k^k^k^k utilise the 13-gate 2x2 multiplier. – John Dvorak – 2013-08-10T06:14:08.940
can I get a clock input, please? Maybe a shift-accumulate approach would lead to a smaller solution – John Dvorak – 2013-08-10T06:24:57.847
@boothby it turns out I can utilise a 13-gate 2x2 multiplier – John Dvorak – 2013-08-10T08:12:34.647
Looks like I mistraced some lines in your original, and it looked like a 2x2 only took 13. It's funny how just knowing the number of operations to shoot for makes it possible to find. I just installed the latest lingeling, and I think I can now optimize the 3x2. – boothby – 2013-08-10T14:39:00.157