30
4
For an N by N image, find a set of pixels such that no separation distance is present more than once. That is, if two pixels are separated by a distance d, then they are the only two pixels that are separated by exactly d (using Euclidean distance). Note that d need not be integer.
The challenge is to find a larger such set than anyone else.
Specification
No input is required - for this contest N will be fixed at 619.
(Since people keep asking - there's nothing special about the number 619. It was chosen to be large enough to make an optimal solution unlikely, and small enough to let an N by N image be displayed without Stack Exchange automatically shrinking it. Images can be displayed full size up to 630 by 630, and I decided to go with the largest prime that doesn't exceed that.)
The output is a space separated list of integers.
Each integer in the output represents one of the pixels, numbered in English reading order from 0. For example for N = 3, the locations would be numbered in this order:
0 1 2
3 4 5
6 7 8
You may output progress information during running if you wish, as long as the final scoring output is easily available. You may output to STDOUT or to a file or whatever is easiest for pasting into the Stack Snippet Judge below.
Example
N = 3
Chosen coordinates:
(0,0)
(1,0)
(2,1)
Output:
0 1 5
Winning
The score is the number of locations in the output. Of those valid answers which have the highest score, the earliest to post output with that score wins.
Your code does not need to be deterministic. You may post your best output.
Related areas for research
(Thanks to Abulafia for the Golomb links)
While neither of these is the same as this problem, they are both similar in concept and may give you ideas on how to approach this:
- Golomb ruler: the 1 dimensional case.
- Golomb rectangle: a 2 dimensional extension of the Golomb ruler. A variant of the NxN (square) case known as Costas array is solved for all N.
Note that the points required for this question are not subject to the same requirements as a Golomb rectangle. A Golomb rectangle extends from the 1 dimensional case by requiring that the vector from each point to each other be unique. This means that there can be two points separated by a distance of 2 horizontally, and also two points separated by a distance of 2 vertically.
For this question, it is the scalar distance that must be unique, so there cannot be both a horizontal and a vertical separation of 2. Every solution to this question will be a Golomb rectangle, but not every Golomb rectangle will be a valid solution to this question.
Upper bounds
Dennis helpfully pointed out in chat that 487 is an upper bound on the score, and gave a proof:
According to my CJam code (
619,2m*{2f#:+}%_&,), there are 118800 unique numbers that can be written as the sum of the squares of two integers between 0 and 618 (both inclusive). n pixels require n(n-1)/2 unique distances between each other. For n = 488, that gives 118828.
So there are 118,800 possible different lengths between all the potential pixels in the image, and placing 488 black pixels would result in 118,828 lengths, which makes it impossible for them all to be unique.
I'd be very interested to hear if anyone has a proof of a lower upper bound than this.
Leaderboard
(Best answer by each user)
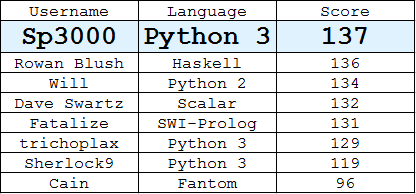
Stack Snippet Judge
canvas=document.getElementById('canvas');ctx=canvas.getContext('2d');information=document.getElementById('information');problemList=document.getElementById('problemList');width=canvas.width;height=canvas.height;area=width*height;function verify(){stop();checkPoints();}function checkPoints(){valid=true;numbers=[];points=[];lengths=[];lengthDetails=[];duplicatedLengths=[];clearCanvas();rawData=pointData.value;splitData=rawData.split(' ');for(i=0;i<splitData.length;i++){datum=splitData[i];if(datum!==''){n=parseInt(datum);if(n>=area||n<0){valid=false;information.innerHTML='Out of range:'+n;break;}if(numbers.indexOf(n)>-1){valid=false;information.innerHTML='Duplicated value:'+n;break;}numbers.push(n);x=n%width;y=Math.floor(n/width);points.push([x,y]);}}if(valid){ctx.fillStyle='black';for(i=0;i<points.length-1;i++){p1=points[i];x1=p1[0];y1=p1[1];drawPoint(x1,y1);for(j=i+1;j<points.length;j++){p2=points[j];x2=p2[0];y2=p2[1];d=distance(x1,y1,x2,y2);duplicate=lengths.indexOf(d);if(duplicate>-1){duplicatedLengths.push(lengthDetails[duplicate]);duplicatedLengths.push([d,[numbers[i],numbers[j]],[x1,y1,x2,y2]]);}lengths.push(d);lengthDetails.push([d,[numbers[i],numbers[j]],[x1,y1,x2,y2]]);}}p=points[points.length-1];x=p[0];y=p[1];drawPoint(x,y);if(duplicatedLengths.length>0){ctx.strokeStyle='red';information.innerHTML='Duplicate lengths shown in red';problemTextList=[];for(i=0;i<duplicatedLengths.length;i++){data=duplicatedLengths[i];length=data[0];numberPair=data[1];coords=data[2];line(coords);specificLineText='<b>'+length+': '+numberPair[0]+' to '+numberPair[1]+'</b> [('+coords[0]+', '+coords[1]+') to ('+coords[2]+', '+coords[3]+')]';if(problemTextList.indexOf(specificLineText)===-1){problemTextList.push(specificLineText);}}problemText=problemTextList.join('<br>');problemList.innerHTML=problemText;}else{information.innerHTML='Valid: '+points.length+' points';}}}function clearCanvas(){ctx.fillStyle='white';ctx.fillRect(0,0,width,height);}function line(coords){x1=coords[0];y1=coords[1];x2=coords[2];y2=coords[3];ctx.beginPath();ctx.moveTo(x1+0.5,y1+0.5);ctx.lineTo(x2+0.5,y2+0.5);ctx.stroke();}function stop(){information.innerHTML='';problemList.innerHTML='';}function distance(x1,y1,x2,y2){xd=x2-x1;yd=y2-y1;return Math.sqrt(xd*xd+yd*yd);}function drawPoint(x,y){ctx.fillRect(x,y,1,1);}<input id='pointData' placeholder='Paste data here' onblur='verify()'></input><button>Verify data</button><p id='information'></p><p id='problemList'></p><canvas id='canvas' width='619' height='619'></canvas>


I would have loved to see a Piet answer here – C5H8NNaO4 – 2015-07-05T08:46:53.727
@C5H8NNaO4 the competition is open ended - no one is anywhere near an optimal solution so there's plenty of room for new answers... – trichoplax – 2015-07-05T13:19:59.847
Since you're offering bounties for both proved upper bound and experimental list of pixels, I assume there is some kind of application to this problem? – Fatalize – 2015-07-05T14:50:44.873
@Fatalize not that I'm aware of, but I'd be fascinated to hear of one. The similar problem Costas array has practical applications listed but I've found nothing on this particular problem.
– trichoplax – 2015-07-05T14:57:51.593(I have a great promising approach that might just stand a chance of winning, but its taking forever to run and might not be ready complete in time!) – Will – 2015-07-09T16:45:53.740
@Will there's a 24 hour grace period after the official bounty deadline, and I'll be waiting for that if there are any answers pending. Hopefully that's enough... – trichoplax – 2015-07-09T20:39:34.817
Also I'll be updating the accepted answer in future if the bountied answer is later beaten - the end of the bounty isn't the end of the competition. – trichoplax – 2015-07-09T20:40:57.380
I'm spent 6 hours and put 77 points that invalidate less than half the space and I don't know how soon I'll get to leave the computer running longer... Here's progress http://i.stack.imgur.com/d1qEi.png (blue squares are invalidated because of distance to point, red squares by symmetry between two points and green squares by both constraints).
– Will – 2015-07-09T21:28:45.403@Will post the code - maybe someone will be able to run it longer... – trichoplax – 2015-07-09T21:34:13.297
1I've been looking at this, and I believe n=487 to be the minimal upper bound on pixels. Out of curiosity, will you accept a proof that there is no lesser upper bound for the bounty? – Mego – 2015-10-15T14:12:51.790
@Mego I had guessed that there would exist an upper bound smaller than 487. If someone posts a valid answer that also contains a valid proof that 487 is minimal, then this proves the bounty cannot be assigned as described, and I will award 300 bounty to the first such proof. – trichoplax – 2015-10-15T14:35:37.897
@trichoplax Ok neat, I've been working on a proof, was curious if the bounty would apply, since it stated specifically an upper bound less than 487. – Mego – 2015-10-15T14:59:26.997
@Mego For any upper bound less than 487, simply a proof that it is an upper bound is sufficient to compete for the bounty. To win the bounty with 487 it will also be required to prove that it is the least possible upper bound (which is what you are working on). In either case the proof must be part of a valid answer to the main question. Hopefully that covers everything for anyone else wishing to compete with you. I didn't want to edit the question just for the bonus bounty as that would bump it to the top of the question list. – trichoplax – 2015-10-15T17:22:19.630
I will be very surprised and impressed if either case is proved (that there is a lower upper bound or that there is not). Hence the size of the bounty... – trichoplax – 2015-10-15T17:24:21.570