Tutte–Coxeter graph

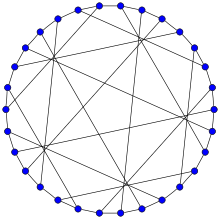
In the mathematical field of graph theory, the Tutte–Coxeter graph or Tutte eight-cage or Cremona–Richmond graph is a 3-regular graph with 30 vertices and 45 edges. As the unique smallest cubic graph of girth 8 it is a cage and a Moore graph. It is bipartite, and can be constructed as the Levi graph of the generalized quadrangle W₂ (known as the Cremona–Richmond configuration). The graph is named after William Thomas Tutte and H. S. M. Coxeter; it was discovered by Tutte (1947) but its connection to geometric configurations was investigated by both authors in a pair of jointly published papers (Tutte 1958; Coxeter 1958a).

Not to be confused with Coxeter graph.

Tutte–Coxeter graph
Named after	W. T. Tutte H. S. M. Coxeter
Vertices	30
Edges	45
Radius	4
Diameter	4
Girth	8
Automorphisms	1440 (Aut(S6))
Chromatic number	2
Chromatic index	3
Book thickness	3
Queue number	2
Properties	Cubic Cage Moore graph Symmetric Distance-regular Distance-transitive Bipartite
Table of graphs and parameters

All the cubic distance-regular graphs are known.[1] The Tutte–Coxeter is one of the 13 such graphs.

It has crossing number 13,[2][3] book thickness 3 and queue number 2.[4]

Constructions and automorphisms

A particularly simple combinatorial construction of the Tutte–Coxeter graph is due to Coxeter (1958b), based on work by Sylvester (1844). In modern terminology, take a complete graph on 6 vertices K₆. It has 15 edges and also 15 perfect matchings. Each vertex of the Tutte–Coxeter graph corresponds to an edge or perfect matching of the K₆, and each edge of the Tutte–Coxeter graph connects a perfect matching of the K₆ to each of its three component edges. By symmetry, each edge of the K₆ belongs to three perfect matchings. Incidentally, this partitioning of vertices into edge-vertices and matching-vertices shows that the Tutte-Coxeter graph is bipartite.

Based on this construction, Coxeter showed that the Tutte–Coxeter graph is a symmetric graph; it has a group of 1440 automorphisms, which may be identified with the automorphisms of the group of permutations on six elements (Coxeter 1958b). The inner automorphisms of this group correspond to permuting the six vertices of the K₆ graph; these permutations act on the Tutte–Coxeter graph by permuting the vertices on each side of its bipartition while keeping each of the two sides fixed as a set. In addition, the outer automorphisms of the group of permutations swap one side of the bipartition for the other. As Coxeter showed, any path of up to five edges in the Tutte–Coxeter graph is equivalent to any other such path by one such automorphism.

The Tutte–Coxeter graph as a building

This graph is the spherical building associated to the symplectic group ${\displaystyle Sp_{4}(\mathbb {F} _{2})}$ (there is an exceptional isomorphism between this group and the symmetric group ${\displaystyle S_{6}}$). More specifically, it is the incidence graph of a generalized quadrangle.

Concretely, the Tutte-Coxeter graph can be defined from a 4-dimensional symplectic vector space V over ${\displaystyle \mathbb {F} _{2}}$ as follows:

• vertices are either nonzero vectors, or isotropic 2-dimensional subspaces,
• there is an edge between a nonzero vector v and an isotropic 2-dimensional subspace ${\displaystyle W\subset V}$ if and only if ${\displaystyle v\in W}$.

Gallery

• 
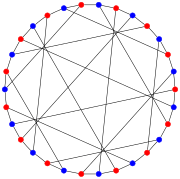  The chromatic number of the Tutte–Coxeter graph is 2.
• 
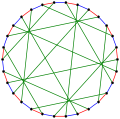  The chromatic index of the Tutte–Coxeter graph is 3.

References

1. Brouwer, A. E.; Cohen, A. M.; and Neumaier, A. Distance-Regular Graphs. New York: Springer-Verlag, 1989.
2. Pegg, E. T.; Exoo, G. (2009). "Crossing Number Graphs". Mathematica Journal. 11. doi:10.3888/tmj.11.2-2.CS1 maint: ref=harv (link)
3. Exoo, G. "Rectilinear Drawings of Famous Graphs".
4. Wolz, Jessica; Engineering Linear Layouts with SAT. Master Thesis, University of Tübingen, 2018

• Coxeter, H. S. M. (1958a). "The chords of the non-ruled quadric in PG(3,3)". Can. J. Math. 10: 484–488. doi:10.4153/CJM-1958-047-0.

• Coxeter, H. S. M. (1958b). "Twelve points in PG(5,3) with 95040 self-transformations". Proceedings of the Royal Society A. 247 (1250): 279–293. doi:10.1098/rspa.1958.0184. JSTOR 100667.

• Sylvester, J. J. (1844). "Elementary researches in the analysis of combinatorial aggregation". Phil. Mag. Series 3. 24: 285–295. doi:10.1080/14786444408644856.

• Tutte, W. T. (1947). "A family of cubical graphs". Proc. Cambridge Philos. Soc. 43 (4): 459–474. doi:10.1017/S0305004100023720.

• Tutte, W. T. (1958). "The chords of the non-ruled quadric in PG(3,3)". Can. J. Math. 10: 481–483. doi:10.4153/CJM-1958-046-3.

External links

• François Labelle. "3D Model of Tutte's 8-cage".
• Weisstein, Eric W. "Levi Graph". MathWorld.
• Exoo, G. "Rectilinear Drawings of Famous Graphs."