Levi graph

In combinatorial mathematics, a Levi graph or incidence graph is a bipartite graph associated with an incidence structure.[1][2] From a collection of points and lines in an incidence geometry or a projective configuration, we form a graph with one vertex per point, one vertex per line, and an edge for every incidence between a point and a line. They are named for Friedrich Wilhelm Levi, who wrote about them in 1942.[1][3]

Levi graph
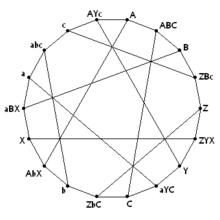The Pappus graph, a Levi graph with 18 vertices formed from the Pappus configuration. Vertices labeled with single letters correspond to points in the configuration; vertices labeled with three letters correspond to lines through three points.
Girth≥ 6
Table of graphs and parameters

The Levi graph of a system of points and lines usually has girth at least six: Any 4-cycles would correspond to two lines through the same two points. Conversely any bipartite graph with girth at least six can be viewed as the Levi graph of an abstract incidence structure.[1] Levi graphs of configurations are biregular, and every biregular graph with girth at least six can be viewed as the Levi graph of an abstract configuration.[4]

Levi graphs may also be defined for other types of incidence structure, such as the incidences between points and planes in Euclidean space. For every Levi graph, there is an equivalent hypergraph, and vice versa.

Examples
  • The Desargues graph is the Levi graph of the Desargues configuration, composed of 10 points and 10 lines. There are 3 points on each line, and 3 lines passing through each point. The Desargues graph can also be viewed as the generalized Petersen graph G(10,3) or the bipartite Kneser graph with parameters 5,2. It is 3-regular with 20 vertices.
  • The Heawood graph is the Levi graph of the Fano plane. It is also known as the (3,6)-cage, and is 3-regular with 14 vertices.
  • The Möbius–Kantor graph is the Levi graph of the Möbius–Kantor configuration, a system of 8 points and 8 lines that cannot be realized by straight lines in the Euclidean plane. It is 3-regular with 16 vertices.
  • The Pappus graph is the Levi graph of the Pappus configuration, composed of 9 points and 9 lines. Like the Desargues configuration there are 3 points on each line and 3 lines passing through each point. It is 3-regular with 18 vertices.
  • The Gray graph is the Levi graph of a configuration that can be realized in as a grid of 27 points and the 27 orthogonal lines through them.
  • The Tutte eight-cage is the Levi graph of the Cremona–Richmond configuration. It is also known as the (3,8)-cage, and is 3-regular with 30 vertices.
  • The four-dimensional hypercube graph is the Levi graph of the Möbius configuration formed by the points and planes of two mutually incident tetrahedra.
  • The Ljubljana graph on 112 vertices is the Levi graph of the Ljubljana configuration.[5]
gollark: Apparently the (or at least a) reason for this problem is that a degree works as a proxy for some minimum standard at stuff like being able to consistently do sometimes-boring things for 4 years, remember information and do things with it, and manage to go to class on time. So it's useful information regardless of whether the employer actually needs your specialized knowledge at all (in many cases, they apparently do not). And they're increasingly common, so *not* having one is an increasing red flag - you may have some sort of objection to the requirement for them, but that can't be distinguished from you just not being able to get one.
gollark: The solution, clearly, is to ban asking people if they have degrees when hiring, and force them to be tested on other things instead.
gollark: That wouldn't destroy it.
gollark: The most feasible way would probably be to deorbit the earth with MANY mass drivers.
gollark: https://qntm.org/destroy

References
  1. Grünbaum, Branko (2006), "Configurations of points and lines", The Coxeter Legacy, Providence, RI: American Mathematical Society, pp. 179–225, MR 2209028. See in particular p. 181.
  2. Polster, Burkard (1998), A Geometrical Picture Book, Universitext, New York: Springer-Verlag, p. 5, doi:10.1007/978-1-4419-8526-2, ISBN 0-387-98437-2, MR 1640615.
  3. Levi, F. W. (1942), Finite Geometrical Systems, Calcutta: University of Calcutta, MR 0006834.
  4. Gropp, Harald (2007), "VI.7 Configurations", in Colbourn, Charles J.; Dinitz, Jeffrey H. (eds.), Handbook of combinatorial designs, Discrete Mathematics and its Applications (Boca Raton) (Second ed.), Chapman & Hall/CRC, Boca Raton, Florida, pp. 353–355.
  5. Conder, Marston; Malnič, Aleksander; Marušič, Dragan; Pisanski, Tomaž; Potočnik, Primož (2002), The Ljubljana Graph (PDF), IMFM Preprint 40-845, University of Ljubljana Department of Mathematics.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.