Teragon

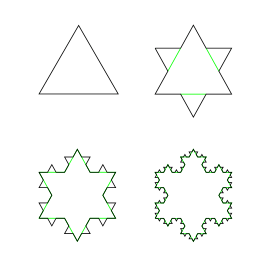
A teragon is a polygon with an infinite number of sides, the most famous example being the Koch snowflake ("triadic Koch teragon"). Typically, a teragon will be bounded by one or more self-similar fractal curves, which are created by replacing each line segment in an initial figure with multiple connected segments, then replacing each of those segments with the same pattern of segments, then repeating the process an infinite number of times for every line segment in the figure.

Not to be confused with Tarragon.

Creating a teragon, the Koch snowflake

Horned triangle or teragonic triangle

[1] Quadratic Koch island/Minkowski fractal

Etymology

To describe the Koch snowflake, Mandelbrot coined the term teragon, which translates literally from the Greek words for "monster curve."[2]

The word "teragon" comes from Greek τέρας (teras), "monster, marvel", + γωνία (gōnía) "corner, angle" (as in poly-gon). By the standards of classical geometry, a teragon like the Koch snowflake was a marvelous or monstrous object requiring new techniques to understand and analyze.

Other examples

The horned triangle, created by erecting a series of smaller triangles on one corner of an equilateral triangle, is another example of a teragon. It is also an example of a rep-tile, or shape that can be completely dissected into smaller copies of itself.

References

1. Albeverio, Sergio; Andrey, Sergio; Giordano, Paolo; and Vancheri, Alberto (1997). The Dynamics of Complex Urban Systems, p.222. Springer. ISBN 9783790819373.
2. Larson, Ron; Hostetler, Robert P.; and Edwards, Bruce H. (1998). Calculus, p.546. 6th edition. Houghton Mifflin. ISBN 9780395869741.

Further reading

• Mandelbrot, B. B. (1982). The Fractal Geometry of Nature. W.H. Freeman and Company. ISBN 0-7167-1186-9.