Supersymmetric theory of stochastic dynamics

Supersymmetric theory of stochastic dynamics or stochastics (STS) is an exact theory of stochastic (partial) differential equations (SDEs), the class of mathematical models with the widest applicability covering, in particular, all continuous time dynamical systems, with and without noise. The main utility of the theory from the physical point of view is a rigorous theoretical explanation of the ubiquitous spontaneous long-range dynamical behavior that manifests itself across disciplines via such phenomena as 1/f, flicker, and crackling noises and the power-law statistics, or Zipf's law, of instantonic processes like earthquakes and neuroavalanches. From the mathematical point of view, STS is interesting because it bridges the two major parts of mathematical physics – the dynamical systems theory and topological field theories. Besides these and related disciplines such as algebraic topology and supersymmetric field theories, STS is also connected with the traditional theory of stochastic differential equations and the theory of pseudo-Hermitian operators.

The theory began with the application of BRST gauge fixing procedure to Langevin SDEs,[1][2] that was later adapted to classical mechanics[3][4][5][6] and its stochastic generalization,[7] higher-order Langevin SDEs,[8] and, more recently, to SDEs of arbitrary form,[9] which allowed to link BRST formalism to the concept of transfer operators and recognize spontaneous breakdown of BRST supersymmetry as a stochastic generalization of dynamical chaos.

The main idea of the theory is to study, instead of trajectories, the SDE-defined temporal evolution of differential forms. This evolution has an intrinsic BRST or topological supersymmetry representing the preservation of topology and/or the concept of proximity in the phase space by continuous time dynamics. The theory identifies a model as chaotic, in the generalized, stochastic sense, if its ground state is not supersymmetric, i.e., if the supersymmetry is broken spontaneously. Accordingly, the emergent long-range behavior that always accompanies dynamical chaos and its derivatives such as turbulence and self-organized criticality can be understood as a consequence of the Goldstone theorem.

History and relation to other theories

The first relation between supersymmetry and stochastic dynamics was established by Giorgio Parisi and Nicolas Sourlas[1][2] who demonstrated that the application of the BRST gauge fixing procedure to Langevin SDEs, i.e., to SDEs with linear phase spaces, gradient flow vector fields, and additive noises, results in N=2 supersymmetric models. Since then, the so-emerged supersymmetry of Langevin SDEs has been studied rather extensively.[10][11][12][13][8] Relations between this supersymmetry and a few physical concepts have been established including the fluctuation dissipation theorems,[13] Jarzynski equality,[14] Onsager principle of microscopic reversibility,[15] solutions of Fokker-Planck equations,[16] self-organization,[17] etc.

Similar approach was used to establish that classical mechanics,[3][4] its stochastic generalization,[7] and higher-order Langevin SDEs[8] also have supersymmetric representations. Real dynamical systems, however, are never purely Langevin or classical mechanical. In addition, physically meaningful Langevin SDEs never break supersymmetry spontaneously. Therefore, for the purpose of the identification of the spontaneous supersymmetry breaking as dynamical chaos, the generalization of the Parisi-Sourlas approach to SDEs of general form is needed. This generalization could come only after a rigorous formulation of the theory of pseudo-Hermitian operators[18] because the stochastic evolution operator is pseudo-Hermitian in the general case. Such generalization[9] showed that all SDEs possess N=1 BRST or topological supersymmetry (TS) and this finding completes the story of relation between supersymmetry and SDEs.

In parallel to the BRST procedure approach to SDEs, mathematicians working in the dynamical systems theory introduced and studied the concept of generalized transfer operator defined for random dynamical systems.[19][20] This concept underlies the most important object of the STS, the stochastic evolution operator, and provides it with a solid mathematical meaning.

STS has a close relation with algebraic topology and its topological sector belongs to the class of models known as Witten-type topological or cohomological field theory.[21][22] [23][24][25][26] As a supersymmetric theory, BRST procedure approach to SDEs can be viewed as one of the realizations of the concept of Nicolai map.[27][28]

Parisi–Sourlas approach to Langevin SDEs

In the context of supersymmetric approach to stochastic dynamics, the term Langevin SDEs denotes SDEs with Euclidean phase space, ${\displaystyle X=\mathbb {R} ^{n}}$, gradient flow vector field, and additive Gaussian white noise,

$${\displaystyle {\dot {x}}(t)=-\partial U(x(t))+(2\Theta )^{1/2}\xi (t),}$$

where ${\displaystyle x\in X}$ , ${\displaystyle \xi \in \mathbb {R} ^{n}}$is the noise variable, ${\displaystyle \Theta }$ is the noise intensity, and ${\displaystyle \partial U(x)}$, which in coordinates ${\displaystyle (\partial U(x))^{i}\equiv \delta ^{ij}\partial _{j}U(x)}$ and ${\displaystyle \partial _{i}U(x)\equiv \partial U(x)/\partial x^{i}}$, is the gradient flow vector field with ${\displaystyle U(x)}$ being the Langevin function often interpreted as the energy of the purely dissipative stochastic dynamical system.

The Parisi-Sourlas method is a way of construction of the path integral representation of the Langevin SDE. It can be thought of as a BRST gauge fixing procedure that uses the Langevin SDE as a gauge condition. Namely, one considers the following functional integral,

$${\displaystyle {\mathcal {W}}=\left\langle \int \dots \int J\left(\prod \nolimits _{\tau }\delta ({\dot {x}}(\tau )-{\mathcal {F}}(x(\tau )))\right)Dx\right\rangle _{\text{noise}},}$$

where ${\displaystyle {\mathcal {F}}}$ denotes the r.h.s. of the Langevin SDE, ${\displaystyle \textstyle \langle \cdot \rangle _{\text{noise}}\equiv \int \dots \int \cdot P(\xi )D\xi }$ is the operation of stochastic averaging with ${\displaystyle P(\xi )\propto e^{-\int _{t'}^{t}d\tau \xi ^{2}(\tau )/2}}$ being the normalized distribution of noise configurations,

${\displaystyle \textstyle J=\operatorname {Det} {\frac {\delta ({\dot {x}}(\tau )-{\mathcal {F}}(x(\tau )))}{\delta x(\tau ')}}}$

is the Jacobian of the corresponding functional derivative, and the path integration is over all closed paths, ${\displaystyle x(t)=x(t')}$, where ${\displaystyle t'}$ and ${\displaystyle t>t'}$are the initial and final moments of temporal evolution.

Topological interpretation

Topological aspects of the Parisi-Sourlas construction can be briefly outlined in the following manner.[21] [29] The delta-functional, i.e., the collection of the infinite number of delta-functions, ensures that only solutions of the Langevin SDE contribute to ${\displaystyle {\mathcal {W}}}$. In the context of BRST procedure, these solutions can be viewed as Gribov copies. Each solution contributes either positive or negative unity: ${\textstyle {\mathcal {W}}=\textstyle \left\langle I_{N}(\xi )\right\rangle _{\text{noise}}}$with ${\textstyle I_{N}(\xi )=\sum _{\text{solutions}}\operatorname {sign} J}$ being the index of the so-called Nicolai map, ${\textstyle \xi =({\dot {x}}+\partial U)/(2\Theta )^{1/2}}$, which in this case is the map from the space of closed paths in ${\textstyle X}$ to the space of noise configurations, a map that provides a noise configuration at which a given closed path is a solution of the Langevin SDE. ${\textstyle I_{N}(\xi )}$ can be viewed as a realization of Poincaré–Hopf theorem on the infinite-dimensional space of close paths with the Langevin SDE playing the role of the vector field and with the solutions of Langevin SDE playing the role of the critical points with index ${\displaystyle \operatorname {sign} J}$. ${\textstyle I_{N}(\xi )}$ is independent of the noise configuration because it is of topological character. The same it true for its stochastic average, ${\displaystyle {\mathcal {W}}}$, which is not the partition function of the model but, instead, its Witten index.

Path integral representation

With the help of a standard field theoretic technique that involves introduction of additional field called Lagrange multiplier, ${\displaystyle B}$, and a pair of fermionic fields called Faddeev–Popov ghosts, ${\displaystyle \chi ,{\bar {\chi }}}$, the Witten index can be given the following form,

$${\displaystyle {\mathcal {W}}=\int \dots \int _{p.b.c.}e^{(Q,\Psi )}D\Phi ,}$$

where ${\displaystyle \Phi }$ denotes collection of all the fields, p.b.c. stands for periodic boundary conditions, the so-called gauge fermion, ${\displaystyle \textstyle \Psi =\int _{t'}^{t}d\tau (\imath _{\dot {x}}-{\bar {d}})(\tau )}$, with ${\displaystyle \textstyle \imath _{\dot {x}}=i{\bar {\chi }}_{j}{\dot {x}}^{j}}$ and ${\textstyle \textstyle {\bar {d}}=-i{\bar {\chi }}_{j}\delta ^{jk}(\partial _{k}U+\Theta iB_{k})}$, and the BRST symmetry defined via its action on arbitrary functional ${\displaystyle A(\Phi )}$ as ${\displaystyle (Q,A(\Phi ))=\textstyle \int _{t'}^{t}d\tau (\chi ^{i}(\tau )\delta /\delta x^{i}(\tau )+B_{i}(\tau )\delta /\delta {\bar {\chi }}_{i}(\tau ))A(\Phi )}$. In the BRST formalism, the Q-exact pieces like, ${\displaystyle (Q,\Psi )}$, serve as gauge fixing tools. Therefore, the path integral expression for ${\displaystyle {\mathcal {W}}}$ can be interpreted as a model whose action contains nothing else but the gauge fixing term. This is a definitive feature of Witten-type topological field theories and in this particular case of BRST procedure approach to SDEs, the BRST symmetry can be also recognized as the topological supersymmetry.[21]

A common way to explain the BRST procedure is to say that the BRST symmetry generates the fermionic version of the gauge transformations, whereas its overall effect on the path integral is to limit the integration only to configurations that satisfy a specified gauge condition. This interpretation also applies to Parisi-Sourlas approach with the deformations of the trajectory and the Langevin SDE playing the roles of the gauge transformations and the gauge condition respectively.

Operator representation

Physical fermions in the high-energy physics and condensed matter models have antiperiodic boundary conditions in time. The unconventional periodic boundary conditions for fermions in the path integral expression for the Witten index is the origin of the topological character of this object. These boundary conditions reveal themselves in the operator representation of the Witten index as the alternating sign operator,

$${\displaystyle {\mathcal {W}}=\operatorname {Tr} (-1)^{\hat {n}}{\hat {\mathcal {M}}}_{tt'},}$$

where ${\textstyle {\hat {n}}}$ is the operator of the number of ghosts/fermions and the finite-time stochastic evolution operator (SEO), ${\textstyle {\hat {\mathcal {M}}}_{tt'}=e^{-(t-t'){\hat {H}}}}$, where,

$${\displaystyle {\hat {H}}={\hat {L}}_{-\partial U}-\Theta {\hat {\triangle }}=[{\hat {d}},{\hat {\bar {d}}}],}$$

is the infinitesimal SEO with ${\displaystyle \textstyle {\hat {L}}}$ being the Lie derivative along the subscript vector field, ${\textstyle {\hat {\triangle }}}$ being the Laplacian, ${\displaystyle \textstyle {\hat {d}}=\chi ^{i}\partial /\partial x^{i}}$ being the exterior derivative, which is the operator representative of the TS, and ${\displaystyle \textstyle {\hat {\bar {d}}}=-(i{\hat {\bar {\chi }}}_{i})\delta ^{ij}(\partial _{j}U+\Theta (i{\hat {B}}_{j}))}$, where ${\displaystyle i{\hat {B}}_{j}=\partial /\partial x^{j}}$ and ${\displaystyle i{\hat {\bar {\chi }}}_{j}=\partial /\partial \chi ^{j}}$ are bosonic and fermionic momenta, and with square brackets denoting bi-graded commutator, i.e., it is an anticommutator if both operators are fermionic (contain odd total number of ${\displaystyle \chi }$'s and ${\displaystyle {\hat {\bar {\chi }}}}$'s) and a commutator otherwise. The exterior derivative and ${\displaystyle \textstyle {\hat {\bar {d}}}}$ are supercharges. They are nilpotent, e.g., ${\displaystyle {\hat {d}}^{2}=0}$, and commutative with the SEO. In other words, Langevin SDEs possess N=2 supersymmetry. The fact that ${\displaystyle \textstyle {\hat {\bar {d}}}}$ is a supercharge is accidental. For SDEs of arbitrary form, this is not true.

Hilbert space

The wavefunctions are functions not only of the bosonic variables, ${\displaystyle x\in X}$, but also of the Grassmann numbers or fermions, ${\displaystyle \chi \in TX}$, from the tangent space of ${\displaystyle X}$. The wavefunctions can be viewed as differential forms on ${\displaystyle X}$ with the fermions playing the role of the differentials ${\displaystyle \chi \equiv dx\wedge }$.[25] The concept of infinitesimal SEO generalizes the Fokker–Planck operator, which is essentially the SEO acting on top differential forms that have the meaning of the total probability distributions. Differential forms of lesser degree can be interpreted, at least locally on ${\displaystyle X}$, as conditional probability distributions.[30] Viewing the spaces of differential forms of all degrees as wavefunctions of the model is a mathematical necessity. Without it, the Witten index representing the most fundamental object of the model—the partition function of the noise—would not exist and the dynamical partition function would not represent the number of fixed points of the SDE (see below). The most general understanding of the wavefunctions is the coordinate-free objects that contain information not only on trajectories but also on the evolution of the differentials and/or Lyapunov exponents.[31]

Relation to nonlinear sigma model and algebraic topology

In Ref.,[25] a model has been introduced that can be viewed as a 1D prototype of the topological nonlinear sigma models (TNSM),[22] a subclass of the Witten-type topological field theories. The 1D TNSM is defined for Riemannian phase spaces while for Euclidean phase spaces it reduces to the Parisi-Sourlas model. Its key difference from STS is the diffusion operator which is the Hodge Laplacian for 1D TNSM and ${\displaystyle \textstyle {\hat {L}}_{e_{a}}{\hat {L}}_{e_{a}}}$for STS . This difference is unimportant in the context of relation between STS and algebraic topology, the relation established by the theory of 1D TNSM (see, e.g., Refs.[25][21]).

The model is defined by the following evolution operator ${\textstyle {\hat {H}}={\hat {L}}_{-\partial U}+\Theta [{\hat {d}},{\hat {d}}^{\dagger }]}$, where ${\textstyle (\partial U)^{i}=g^{ij}\partial _{j}U}$ with ${\textstyle g}$ being the metric, ${\textstyle [{\hat {d}},{\hat {d}}^{\dagger }]}$ is the Hodge Laplacian, and the differential forms from the exterior algebra of the phase space, ${\textstyle \Omega (X)}$, are viewed as wavefunctions. There exists a similarity transformation, ${\displaystyle {\hat {H}}\to {\hat {H}}_{U}=e^{U/2\Theta }{\hat {H}}e^{-U/2\Theta }}$, that brings the evolution operator to the explicitly Hermitian form ${\displaystyle {\hat {H}}_{U}=\Theta [{\hat {d}}_{U},{\hat {d}}_{U}^{\dagger }]}$ with ${\displaystyle {\hat {d}}_{U}=e^{U/2\Theta }{\hat {d}}e^{-U/2\Theta }=\chi ^{i}(\partial /\partial x^{i}-\partial _{i}U/2\Theta )}$. In the Euclidean case, ${\displaystyle {\hat {H}}_{U}}$ is the Hamiltonian of a N=2 supersymmetric quantum mechanics. One can introduce two Hermitian operators, ${\displaystyle {\hat {q}}_{1}=({\hat {d}}_{U}+{\hat {d}}_{U}^{\dagger })/2^{1/2}}$ and ${\displaystyle {\hat {q}}_{2}=i({\hat {d}}_{U}-{\hat {d}}_{U}^{\dagger })/2^{1/2}}$, such that ${\displaystyle {\hat {H}}_{U}=\Theta {\hat {q}}_{1}^{2}=\Theta {\hat {q}}_{2}^{2}}$ . This demonstrates that the spectrum of ${\displaystyle {\hat {H}}_{U}}$ and/or ${\displaystyle {\hat {H}}}$ is real and nonnegative. This is also true for SEOs of Langevin SDEs. For the SDEs of arbitrary form, however, this is no longer true as the eigenvalues of the SEO can be negative and even complex, which actually allows for the TS to be broken spontanenously.

The following properties of the evolution operator of 1D TNSM hold even for the SEO of the SDEs of arbitrary form. The evolution operator commutes with the operator of the degree of differential forms. As a result, ${\displaystyle \textstyle {\hat {H}}={\hat {H}}^{(\dim X)}\oplus \dots \oplus {\hat {H}}^{(0)}}$, where ${\displaystyle \textstyle {\hat {H}}^{(k)}={\hat {H}}|_{\Omega ^{(k)}}}$ and ${\displaystyle \Omega ^{(n)}(X)}$ is the space of differential forms of degree ${\displaystyle n}$. Furthermore, due to the presence of TS, ${\textstyle \Omega (X)={\mathcal {H}}\oplus {\mathcal {N}}\oplus ({\hat {d}}{\mathcal {N}})}$, where ${\textstyle {\mathcal {H}}}$ are the supersymmetric eigenstates, ${\textstyle \theta 's}$, non-trivial in de Rham cohomology whereas the rest are the pairs of non-supersymmetric eigenstates of the form ${\textstyle |\vartheta \rangle }$ and ${\textstyle {\hat {d}}|\vartheta \rangle }$. All supersymmetric eigenstates have exactly zero eigenvalue and, barring accidental situations, all non-supersymmetric states have non-zero eigenvalues. Non-supersymmetric pairs of eigenstates do not contribute to the Witten index, which equals the difference in the numbers of the supersymmetric states of even and odd degrees, ${\textstyle {\mathcal {W}}=\#\{{\text{even }}\theta 's\}-\#\{{\text{odd }}\theta 's\}.}$For compact ${\displaystyle X}$, each de Rham cohomology class provides one supersymmetric eigenstate and the Witten index equals the Euler characteristic of the phase space.

BRST procedure for SDEs of arbitrary form

The Parisi-Sourlas method of BRST procedure approach to Langevin SDEs have also been adapted to classical mechanics,[3] stochastic generalization of classical mechanics,[7] higher order Langevin SDEs,[8] and, more recently, to SDEs of arbitrary form.[9] While there exist standard techniques that allow to consider models with colored noises, higher-dimensional "base spaces" described by partial SDEs etc., the key elements of STS can be discussed using the following basic class of SDEs,

$${\displaystyle {\dot {x}}(t)=F(x(t))+(2\Theta )^{1/2}e_{a}(x(t))\xi ^{a}(t),}$$

where ${\textstyle x\in X}$ is a point in the phase space assumed for simplicity a closed topological manifold, ${\displaystyle F(x)\in TX_{x}}$ is a sufficiently smooth vector field, called flow vector field, from the tangent space of ${\displaystyle X}$, and ${\displaystyle e_{a}\in TX,a=1,\ldots ,\dim X}$ is a set of sufficiently smooth vector fields that specify how the system is coupled to the noise, which is called additive/multiplicative depending on whether ${\displaystyle e_{a}}$'s are independent/dependent on the position on ${\displaystyle X}$.

Ambiguity of path integral representation and Ito–Stratonovich dilemma

BRST gauge fixing procedure goes along the same lines as in case of Langevin SDEs. The topological interpretation of the BRST procedure is just the same and the path integral representation of the Witten index is defined by the gauge fermion, ${\displaystyle \textstyle \Psi }$, given by the same expression but with the generalized version of ${\textstyle \textstyle {\bar {d}}=\imath _{F}-\Theta \imath _{e_{a}}(Q,\imath _{e_{a}})}$. There is one important subtlety, however, that appears on the way to the operator representation of the model. Unlike for Langevin SDEs, classical mechanics, and other SDEs with additive noises, the path integral representation of the finite-time SEO is an ambiguous object. This ambiguity originates from non-commutativity of momenta and position operators, e.g., ${\displaystyle {\hat {B}}{\hat {x}}\neq {\hat {x}}{\hat {B}}}$. As a result, ${\displaystyle B(\tau )x(\tau )}$ in the path integral representation has a whole one-parameter family of possible interpretations in the operator representation, ${\displaystyle (\alpha {\hat {B}}{\hat {x}}+(1-\alpha ){\hat {x}}{\hat {B}})|\psi (\tau )\rangle }$, where ${\displaystyle |\psi (\tau )\rangle }$ denotes an arbitrary wavefunction. Accordingly, there is a whole ${\displaystyle \alpha }$-family of infinitesimal SEOs,

$${\displaystyle {\hat {H}}_{\alpha }={\hat {L}}_{F}-\Theta {\hat {L}}_{e_{a}}{\hat {L}}_{e_{a}}=[{\hat {d}},{\hat {\bar {d}}}_{\alpha }],}$$

with ${\displaystyle \textstyle {\hat {\bar {d}}}_{\alpha }={\hat {\imath }}_{F_{\alpha }}-\Theta {\hat {\imath }}_{e_{a}}{\hat {L}}_{e_{a}}}$, ${\displaystyle {\hat {\imath }}_{F_{\alpha }}}$ being the interior multiplication by the subscript vector field, and the "shifted" flow vector field being ${\displaystyle \textstyle F_{\alpha }=F-\Theta (2\alpha -1)(e_{a}\cdot \partial )e_{a}}$. Noteworthy, unlike in Langevin SDEs, ${\displaystyle {\hat {\bar {d}}}_{\alpha }}$ is not a supercharge and STS cannot be identified as a N=2 supersymmetric theory in the general case.

The path integral representation of stochastic dynamics is equivalent to the traditional understanding of SDEs as of a continuous time limit of stochastic difference equations where different choices of parameter ${\displaystyle \alpha }$ are called "interpretations" of SDEs. The choice ${\displaystyle \alpha =1/2}$, for which ${\displaystyle \textstyle F_{1/2}=F}$ and which is known in quantum theory as Weyl symmetrization rule, is known as the Stratonovich interpretation, whereas ${\displaystyle \alpha =1}$ as the Ito interpretation. While in quantum theory the Weyl symmetrization is preferred because it guaranties hermiticity of Hamiltonians, in STS the Weyl-Stratonovich approach is preferred because it corresponds to the most natural mathematical meaning of the finite-time SEO discussed below—the stochastically averaged pullback induced by the SDE-defined diffeomorphisms.

Eigensystem of stochastic evolution operator

The three possible types of SEO spectra on a 3D sphere. Each line of triples of graphs represents ${\displaystyle spec{\hat {H}}^{(n)},}$ ${\displaystyle n=0,...3}$. for the three types of spectra. Black dots at the origin for the first and the last lines represent supersymmetric eigenstates from the zeroth and the third cohomologies of the 3 sphere. For types b and c, the (fastest growing) ground (eigen)states are non-supersymmetric because they have non-zero eigenvalues. TS is broken spontaneously. Vertical arrowed lines visualize supersymmetry operator.

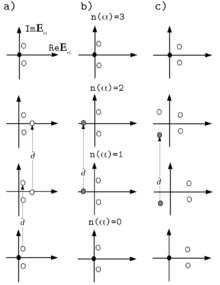
As compared to the SEO of Langevin SDEs, the SEO of a general form SDE is pseudo-Hermitian.[18] As a result, the eigenvalues of non-supersymmetric eigenstates are not restricted to be real positive, whereas the eigenvalues of supersymmetric eigenstates are still exactly zero. Just like for Langevin SDEs and nonlinear sigma model, the structure of the eigensystem of the SEO reestablishes the topological character of the Witten index: the contributions from the non-supersymmetric pairs of eigenstates vanish and only supersymmetric states contribute the Euler characteristic of (closed) ${\displaystyle X}$. Among other properties of the SEO spectra is that ${\displaystyle \textstyle {\hat {H}}^{(\operatorname {dim} X)}}$ and ${\displaystyle \textstyle {\hat {H}}^{(0)}}$ never break TS, i.e., ${\displaystyle \textstyle Re(\operatorname {spec} {\hat {H}}^{(\operatorname {dim} X)})\geq 0}$. As a result, there are three major types of the SEO spectra presented in the figure on the right. The two types that have negative (real parts of) eigenvalues correspond to the spontaneously broken TS. All types of the SEO spectra are realizable as can be established, e.g., from the exact relation between the theory of kinematic dynamo and STS.[32]

STS without BRST procedure

The mathematical meaning of stochastic evolution operator

The finite-time SEO can be obtained in another, more mathematical way based on the idea to study the SDE-induced actions on differential forms directly, without going through the BRST gauge fixing procedure. The so-obtained finite-time SEO is known in dynamical systems theory as the generalized transfer operator[19][20] and it has also been used in the classical theory of SDEs (see, e.g., Refs.[33][34] ). The contribution to this construction from STS[9] is the exposition of the supersymmetric structure underlying it and establishing its relation to the BRST procedure for SDEs.

Namely, for any configuration of the noise, ${\displaystyle \xi }$, and an initial condition, ${\displaystyle x(t')=x'\in X}$, SDE defines a unique solution/trajectory, ${\displaystyle x(t)\in X}$. Even for noise configurations that are non-differentiable with respect to time, ${\displaystyle t}$, the solution is differentiable with respect to the initial condition, ${\displaystyle x'}$.[35] In other words, SDE defines the family of the noise-configuration-dependent diffeomorphisms of the phase space to itself, ${\displaystyle M_{tt'}:X\to X}$. This object can be understood as a collection and/or definition of all the noise-configuration-dependent trajectories, ${\displaystyle x(t)=M_{tt'}(x')}$. The diffeomorphisms induce actions or pullbacks, ${\displaystyle \textstyle M_{t't}^{*}:\Omega (X)\to \Omega (X)}$. Unlike, say, trajectories in ${\displaystyle X}$, pullbacks are linear objects even for nonlinear ${\displaystyle X}$. Linear objects can be averaged and averaging ${\displaystyle M_{t't}^{*}}$ over the noise configurations, ${\displaystyle \xi }$, results in the finite-time SEO which is unique and corresponds to the Weyl-Stratonovich interpretation of the BRST procedure approach to SDEs, ${\displaystyle {\hat {\mathcal {M}}}_{tt'}=\langle M_{t't}^{*}\rangle _{\text{noise}}=e^{-(t-t'){\hat {H}}_{1/2}}}$.

Within this definition of the finite-time SEO, the Witten index can be recognized as the sharp trace of the generalized transfer operator.[19][20] It also links the Witten index to the Lefschetz index,${\textstyle \textstyle I_{L}=\operatorname {Tr} (-1)^{\hat {n}}M_{t't}^{*}=\sum _{x\in \operatorname {fix} M_{tt'}}\operatorname {sign} \operatorname {det} (\delta _{j}^{i}-\partial M_{tt'}^{i}(x)/\partial x^{j})}$, a topological constant that equals the Euler characteristic of the (closed) phase space. Namely, ${\textstyle \textstyle {\mathcal {W}}=\operatorname {Tr} (-1)^{\hat {n}}\langle M_{t't}^{*}\rangle _{\text{noise}}=\langle \operatorname {Tr} (-1)^{\hat {n}}M_{t't}^{*}\rangle _{\text{noise}}=I_{L}}$.

The meaning of supersymmetry and the butterfly effect

The N=2 supersymmetry of Langevin SDEs has been linked to the Onsager principle of microscopic reversibility[15] and Jarzynski equality.[14] In classical mechanics, a relation between the corresponding N=2 supersymmetry and ergodicity has been proposed.[6] In general form SDEs, where physical arguments may not be applicable, a lower level explanation of the TS is available. This explanation is based on understanding of the finite-time SEO as a stochastically averaged pullback of the SDE-defined diffeomorphisms (see subsection above). In this picture, the question of why any SDE has TS is the same as the question of why exterior derivative commutes with the pullback of any diffeomorphism. The answer to this question is differentiability of the corresponding map. In other words, the presence of TS is the algebraic version of the statement that continuous-time flow preserves continuity of ${\displaystyle X}$. Two initially close points will remain close during evolution, which is just yet another way of saying that ${\displaystyle M_{tt'}}$ is a diffeomorphism.

In deterministic chaotic models, initially close points can part in the limit of infinitely long temporal evolution. This is the famous butterfly effect, which is equivalent to the statement that ${\displaystyle M_{tt'}}$ losses differentiability in this limit. In algebraic representation of dynamics, the evolution in the infinitely long time limit is described by the ground state of the SEO and the butterfly effect is equivalent to the spontaneous breakdown of TS, i.e., to the situation when the ground state is not supersymmetric. Noteworthy, unlike traditional understanding of deterministic chaotic dynamics, the spontaneous breakdown of TS works also for stochastic cases. This is the most important generalization because deterministic dynamics is, in fact, a mathematical idealization. Real dynamical systems cannot be isolated from their environments and thus always experience stochastic influence.

Spontaneous supersymmetry breaking and dynamical chaos

BRST gauge fixing procedure applied to SDEs leads directly to the Witten index. The Witten index is of topological character and it does not respond to any perturbation. In particular, all response correlators calculated using the Witten index vanish. This fact has a physical interpretation within the STS: the physical meaning of the Witten index is the partition function of the noise[30] and since there is no backaction from the dynamical system to the noise, the Witten index has no information on the details of the SDE. In contrast, the information on the details of the model is contained in the other trace-like object of the theory, the dynamical partition function,

$${\displaystyle {\mathcal {Z}}_{tt'}=\int \dots \int _{a.p.b.c.}e^{(Q,\Psi )}D\Phi =\operatorname {Tr} {\hat {\mathcal {M}}}_{tt'},}$$

where a.p.b.c. denotes antiperiodic boundary conditions for the fermionic fields and periodic boundary conditions for bosonic fields. In the standard manner, the dynamical partition function can be promoted to the generating functional by coupling the model to external probing fields. For a wide class of models, dynamical partition function provides lower bound for the stochastically averaged number of fixed points of the SDE-defined diffeomorphisms,

$${\displaystyle \left.{\mathcal {Z}}_{tt'}\right|_{t-t'\to \infty }=\sum \nolimits _{p}e^{-(t-t'){\mathsf {E}}_{p}}\leq \langle \#\{{\text{fixed points of }}M_{t't}\}\rangle _{\text{noise}}\propto e^{(t-t')S}.}$$

Here, index ${\displaystyle p}$ runs over "physical states", i.e., the eigenstates that grow fastest with the rate of the exponential growth given as,${\textstyle \Gamma _{g}=-\min _{\alpha }\operatorname {Re} {\mathsf {E}}_{\alpha }\geq 0}$, and parameter ${\displaystyle S}$ can be viewed as stochastic version of dynamical entropy such as topological entropy. Positive entropy is one of the key signatures of deterministic chaos. Therefore, the situation with positive ${\displaystyle \Gamma _{g}}$ must be identified as chaotic in the generalized, stochastic sense as it implies positive entropy: ${\displaystyle 0<\Gamma _{g}\leq S}$. At the same time, positive ${\displaystyle \Gamma _{g}}$ implies that TS is broken spontaneously, that is, the ground state in not supersymmetric because its eigenvalue is not zero. In other words, positive dynamical entropy is a reason to identify spontaneous TS breaking as the stochastic generalization of the concept of dynamical chaos. Noteworthy, Langevin SDEs are never chaotic because the spectrum of their SEO is real non-negative.

The complete list of reasons why spontaneous TS breaking must be viewed as the stochastic generalization of the concept of dynamical chaos is as follows.

• Positive dynamical entropy.
• According to the Goldstone's theorem, spontaneous TS breaking must tailor a long-range dynamical behavior, one of the manifestations of which is the butterfly effect discussed above in the context of the meaning of TS.
• From the properties of the eigensystem of SEO, TS can be spontaneously broken only if ${\displaystyle \dim X\geq 3}$. This conclusion can be viewed as the stochastic generalization of the Poincare–Bendixson theorem for deterministic chaos.
• In the deterministic case, integrable models in the sense of dynamical systems have well-defined global stable and unstable manifolds of ${\displaystyle F}$. The bras/kets of the global ground states of such models are the Poincare duals of the global stable/unstable manifolds. These ground states are supersymmetric so that TS is not broken spontaneously. On the contrary, when the model is non-integrable or chaotic, its global (un)stable manifolds are not well-defined topological manifolds, but rather have a fractal, self-recurrent structure that can be captured using the concept of branching manifolds.[36] Wavefunctions that can represent such manifolds cannot be supersymmetric. Therefore, TS breaking is intrinsically related to the concept of non-integrability in the sense of dynamical systems, which is actually yet another widely accepted definition of deterministic chaos.

All the above features of TS breaking work for both deterministic and stochastic models. This is in contrast with the traditional deterministic chaos whose trajectory-based properties such as the topological mixing cannot in principle be generalized to stochastic case because, just like in quantum dynamics, all trajectories are possible in the presence of noise and, say, the topological mixing property is satisfied trivially by all models with non-zero noise intensity.

STS as a topological field theory

The square acbd represents an instanton, i.e, the family of trajectories of deterministic flow (dotted arrowed curves) leading from one critical point (b) to another (a). The bra/ket (${\displaystyle \langle a|}$/${\displaystyle |b\rangle }$) of the locally supersymmetric ground states (vacua) corresponding to these critical points are the Poincare duals of the local unstable/stable manifolds. Operators ${\displaystyle {\hat {O}}_{1,2}}$ are Poincare duals of vertical/horizontal lines. The value of the instantonic matrix element is the intersection number (the difference in the numbers of positive (black) and negative (white) intersections). It is invariant under the temporal evolution due to the flow, ${\displaystyle {\hat {O}}_{1}(0)\to {\hat {O}}_{1}(t)}$ .

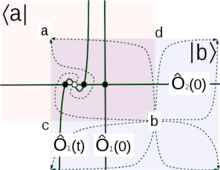
The topological sector of STS can be recognized as a member of the Witten-type topological field theories.[21][22][24][25][26] In other words, some objects in STS are of topological character with the Witten index being the most famous example. There are other classes of topological objects. One class of objects is related to instantons, i.e., transient dynamics. Crumpling paper, protein folding, and many other nonlinear dynamical processes in response to quenches, i.e., to external (sudden) changes of parameters, can be recognized as instantonic dynamics. From the mathematical point of view, instantons are families of solutions of deterministic equations of motion, ${\displaystyle {\dot {x}}=F}$, that lead from, say, less stable fixed point of ${\displaystyle F}$ to a more stable fixed point. Certain matrix elements calculated on instantons are of topological nature. An example of such matrix elements can be defined for a pair of critical points, ${\displaystyle a}$ and ${\displaystyle b}$, with ${\displaystyle a}$ being more stable than ${\displaystyle b}$,

$${\displaystyle \left.\int \dots \int _{x(\pm \infty )=a,b}\left(\prod \nolimits _{i}O_{i}(t_{i})\right)e^{({\mathcal {Q}},\Psi )}D\Phi \right|_{\Theta \to 0}=\langle a|{\mathcal {T}}\left(\prod \nolimits _{i}{\hat {O}}_{i}(t_{i})\right)|b\rangle .}$$

Here ${\displaystyle \langle a|}$ and ${\displaystyle |b\rangle }$ are the bra and ket of the corresponding perturbative supersymmetric ground states, or vacua, which are the Poincare duals of the local stable and unstable manifolds of the corresponding critical point; ${\displaystyle {\mathcal {T}}}$ denotes chronological ordering; ${\displaystyle O}$'s are observables that are the Poincare duals of some closed submanifolds in ${\displaystyle X}$; ${\displaystyle {\hat {O}}(t)={\hat {\mathcal {M}}}_{t_{0},t}{\hat {O}}{\hat {\mathcal {M}}}_{t,t_{0}}}$ are the observables in the Heisenberg representation with ${\displaystyle t_{0}}$ being an unimportant reference time moment. The critical points have different indexes of stability so that the states ${\displaystyle |a\rangle }$ and ${\displaystyle |b\rangle }$ are topologically inequivalent as they represent unstable manifolds of different dimensionalities. The above matrix elements are independent of ${\displaystyle t_{i}'s}$ as they actually represent the intersection number of ${\displaystyle O}$-manifolds on the instanton as exemplified in the figure.

The above instantonic matrix elements are exact only in the deterministic limit. In the general stochastic case, one can consider global supersymmetric states, ${\displaystyle \theta }$'s, from the De Rham cohomology classes of ${\displaystyle X}$ and observables, ${\displaystyle \gamma }$, that are Poincare duals of closed manifolds non-trivial in homology of ${\displaystyle X}$. The following matrix elements, ${\displaystyle \textstyle \langle \theta _{\alpha }|{\mathcal {T}}\left(\prod \nolimits _{i}{\hat {\gamma }}_{i}(t_{i})\right)|\theta _{\beta }\rangle ,}$ are topological invariants representative of the structure of De Rham cohomology ring of ${\displaystyle X}$.

Applications

Supersymmetric theory of stochastic dynamics can be interesting in different ways. For example, STS offers a promising realization of the concept of supersymmetry. In general, there are two major problems in the context of supersymmetry. The first is establishing connections between this mathematical entity and the real world. Within STS, supersymmetry is the most common symmetry in nature because it is pertinent to all continuous time dynamical systems. The second is the spontaneous breakdown of supersymmetry. This problem is particularly important for particle physics because supersymmetry of elementary particles, if exists at extremely short scale, must be broken spontaneously at large scale. This problem is nontrivial because supersymmetries are hard to break spontaneously, the very reason behind the introduction of soft or explicit supersymmetry breaking.[37] Within STS, spontaneous breakdown of supersymmetry is indeed a nontrivial dynamical phenomenon that has been variously known across disciplines as chaos, turbulence, self-organized criticality etc.

A few more specific applications of STS are as follows.

Classification of stochastic dynamics

Stochastic dynamical systems can be classified according to whether TS is spontaneously broken or not (ordered/symmetric) and whether the flow vector field is integrable or non-integrable (sometimes chaotic). Symmetric phase can be identified as thermal equilibrium (T). Ordered non-integrable phase can be called chaos (C) because it hosts conventional deterministic chaos. Ordered integrable phase can be called noise-induced chaos (N) because TS breaking involves anti-instantons that disappear in the deterministic limit. The N-phase is also known in the literature as self-organized criticality.

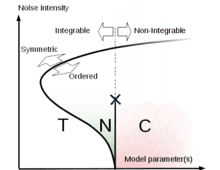
STS provides classification for stochastic models depending on whether TS is broken and integrability of flow vector field. In can be exemplified as a part of the general phase diagram at the border of chaos (see figure on the right). The phase diagram has the following properties:

• For physical models, TS gets restored eventually with the increase of noise intensity.
• Symmetric phase can be called thermal equilibrium or T-phase because the ground state is the supersymmetric state of steady-state total probability distribution.
• In the deterministic limit, ordered phase is equivalent to deterministic chaotic dynamics with non-integrable flow.
• Ordered non-integrable phase can be called chaos or C-phase because ordinary deterministic chaos belongs to it.
• Ordered integrable phase can be called noise-induced chaos or N-phase because it disappears in the deterministic limit. TS is broken by the condensation of (anti-)instantons (see below).
• At stronger noises, the sharp N-C boundary must smear out into a crossover because (anti-)instantons lose their individuality and it is hard for an external observer to tell one tunneling process from another.

Demystification of self-organized criticality

Many sudden (or instantonic) processes in nature, such as, e.g., crackling noise, exhibit scale-free statistics often called the Zipf's law. As an explanation for this peculiar spontaneous dynamical behavior, it was proposed to believe that some stochastic dynamical systems have a tendency to self-tune themselves into a critical point, the phenomenological approach known as self-organized criticality (SOC).[38] STS offers an alternative perspective on this phenomenon.[39] Within STS, SOC is nothing more than dynamics in the N-phase. Specifically, the definitive feature of the N-phase is the peculiar mechanism of the TS breaking. Unlike in the C-phase, where the TS is broken by the non-integrability of the flow, in the N-phase, the TS is spontaneously broken due to the condensation of the configurations of instantons and noise-induced antiinstantons, i.e., time-reversed instantons. These processes can be roughly interpreted as the noise-induced tunneling events between, e.g., different attractors. Qualitatively, the dynamics in the N-phase appears to an external observer as a sequence of sudden jumps or "avalanches" that must exhibit a scale-free behavior/statistics as a result of the Goldstone theorem. This picture of dynamics in the N-phase is exactly the dynamical behavior that the concept of SOC was designed to explain. In contrast with the original understanding of SOC,[40] its STS interpretation has little to do with the traditional critical phenomena theory where scale-free behavior is associated with unstable fixed points of the renormalization group flow.

Kinematic dynamo theory

Magnetohydrodynamical phenomenon of kinematic dynamo can also be identified as the spontaneous breakdown of TS.[32] This result follows from equivalence between the evolution operator of the magnetic field and the SEO of the corresponding SDE describing the flow of the background matter. The so emerged STS-kinematic dynamo correspondence proves, in particular, that both types of TS breaking spectra are possible, with the real and complex ground state eigenvalues, because kinematic dynamo with both types of the fastest growing eigenmodes are known.[41]

Transient dynamics

It is well known that various types of transient dynamics, such as quenches, exhibit spontaneous long-range behavior. In case of quenches across phase transitions, this behavior is often attributed to the proximity of criticality. Quenches that do not exhibit a phase transition are also known to exhibit long-range characteristics, with the best known examples being the Barkhausen effect and the various realizations of the concept of crackling noise. It is intuitively appealing that theoretical explanations for the scale-free behavior in quenches must be the same for all quenches, regardless of whether or not it produces a phase transition; STS offers such an explanation. Namely, transient dynamics is essentially a composite instanton and TS is intrinsically broken within instantons. Even though TS breaking within instantons is not exactly due to the phenomenon of the spontaneous breakdown of a symmetry by a global ground state, this effective TS breaking must also result in a scale-free behavior. This understanding is supported by the fact that condensed instantons lead to appearance of logarithms in the correlation functions.[42] This picture of transient dynamics explains computational efficiency of the digital memcomputing machines.[43]

Low energy effective theories for dynamical chaos

In physics, spontaneous symmetry breaking is known as "ordering". For example, the spontaneous breakdown of translational symmetry in a liquid is the mathematical essence of crystallization or spatial "ordering" of molecules into a lattice. Therefore, spontaneous TS breaking picture of chaotic dynamics is in a certain sense opposite to the semantics of word "chaos". Due to its temporal character, it is actually Chronos, not Chaos, that appears to be the primordial Greek deity closest in its spirit to the TS breaking order. Perhaps, a more accurate identifier than "chaos" should be coined for TS breaking in the future. As of this moment, this qualitatively new understanding of dynamical chaos already points into a research direction that may lead to resolutions of some important problems such as turbulence and neurodynamics. Namely, as in case of any other "ordering", a simplified yet accurate description of chaotic dynamics can be achieved in terms of the low-energy effective theory for an order parameter. While the low-energy effective description of chaotic dynamics may be very case specific, its order parameter must always be a representative of the gapless fermions or goldstinos of the spontaneously broken TS.

References

1. Parisi, G.; Sourlas, N. (1979). "Random Magnetic Fields, Supersymmetry, and Negative Dimensions". Physical Review Letters. 43 (11): 744–745. Bibcode:1979PhRvL..43..744P. doi:10.1103/PhysRevLett.43.744.
2. Parisi, G. (1982). "Supersymmetric field theories and stochastic differential equations". Nuclear Physics B. 206 (2): 321–332. Bibcode:1982NuPhB.206..321P. doi:10.1016/0550-3213(82)90538-7.
3. Gozzi, E.; Reuter, M. (1990). "Classical mechanics as a topological field theory". Physics Letters B. 240 (1–2): 137–144. Bibcode:1990PhLB..240..137G. doi:10.1016/0370-2693(90)90422-3.
4. Niemi, A. J. (1995). "A lower bound for the number of periodic classical trajectories". Physics Letters B. 355 (3–4): 501–506. Bibcode:1995PhLB..355..501N. doi:10.1016/0370-2693(95)00780-o.
5. Niemi, A. J.; Pasanen, P. (1996-10-03). "Topological σ-model, Hamiltonian dynamics and loop space Lefschetz number". Physics Letters B. 386 (1): 123–130. arXiv:hep-th/9508067. Bibcode:1996PhLB..386..123N. doi:10.1016/0370-2693(96)00941-0.
6. Gozzi, E.; Reuter, M. (1989-12-28). "Algebraic characterization of ergodicity". Physics Letters B. 233 (3): 383–392. Bibcode:1989PhLB..233..383G. doi:10.1016/0370-2693(89)91327-0.
7. Tailleur, J.; Tănase-Nicola, S.; Kurchan, J. (2006-02-01). "Kramers Equation and Supersymmetry". Journal of Statistical Physics. 122 (4): 557–595. arXiv:cond-mat/0503545. Bibcode:2006JSP...122..557T. doi:10.1007/s10955-005-8059-x. ISSN 0022-4715.
8. Kleinert, H.; Shabanov, S. V. (1997-10-27). "Supersymmetry in stochastic processes with higher-order time derivatives". Physics Letters A. 235 (2): 105–112. arXiv:quant-ph/9705042. Bibcode:1997PhLA..235..105K. doi:10.1016/s0375-9601(97)00660-9.
9. Ovchinnikov, I. V. (2016-03-28). "Introduction to Supersymmetric Theory of Stochastics". Entropy. 18 (4): 108. arXiv:1511.03393. Bibcode:2016Entrp..18..108O. doi:10.3390/e18040108.
10. Cecotti, S; Girardello, L (1983-01-01). "Stochastic and parastochastic aspects of supersymmetric functional measures: A new non-perturbative approach to supersymmetry". Annals of Physics. 145 (1): 81–99. Bibcode:1983AnPhy.145...81C. doi:10.1016/0003-4916(83)90172-0.
11. Zinn-Justin, J. (1986-09-29). "Renormalization and stochastic quantization". Nuclear Physics B. 275 (1): 135–159. Bibcode:1986NuPhB.275..135Z. doi:10.1016/0550-3213(86)90592-4.
12. Dijkgraaf, R.; Orlando, D.; Reffert, S. (2010-01-11). "Relating field theories via stochastic quantization". Nuclear Physics B. 824 (3): 365–386. arXiv:0903.0732. Bibcode:2010NuPhB.824..365D. doi:10.1016/j.nuclphysb.2009.07.018.
13. Kurchan, J. (1992-07-01). "Supersymmetry in spin glass dynamics". Journal de Physique I. 2 (7): 1333–1352. Bibcode:1992JPhy1...2.1333K. doi:10.1051/jp1:1992214. ISSN 1155-4304.
14. Mallick, K.; Moshe, M.; Orland, H. (2007-11-13). "Supersymmetry and Nonequilibrium Work Relations". arXiv:0711.2059 [cond-mat.stat-mech].
15. Gozzi, E. (1984). "Onsager principle of microscopic reversibility and supersymmetry". Physical Review D. 30 (6): 1218–1227. Bibcode:1984PhRvD..30.1218G. doi:10.1103/physrevd.30.1218.
16. Bernstein, M. (1984). "Supersymmetry and the Bistable Fokker-Planck Equation". Physical Review Letters. 52 (22): 1933–1935. Bibcode:1984PhRvL..52.1933B. doi:10.1103/physrevlett.52.1933.
17. Olemskoi, A. I; Khomenko, A. V; Olemskoi, D. A (2004-02-01). "Field theory of self-organization". Physica A: Statistical Mechanics and Its Applications. 332: 185–206. Bibcode:2004PhyA..332..185O. doi:10.1016/j.physa.2003.10.035.
18. Mostafazadeh, A. (2002-07-19). "Pseudo-Hermiticity versus PT-symmetry III: Equivalence of pseudo-Hermiticity and the presence of antilinear symmetries". Journal of Mathematical Physics. 43 (8): 3944–3951. arXiv:math-ph/0203005. Bibcode:2002JMP....43.3944M. doi:10.1063/1.1489072. ISSN 0022-2488.
19. Reulle, D. (2002). "Dynamical Zeta Functions and Transfer Operators" (PDF). Notices of the AMS. 49 (8): 887.
20. Ruelle, D. (1990-12-01). "An extension of the theory of Fredholm determinants". Publications Mathématiques de l'Institut des Hautes Études Scientifiques. 72 (1): 175–193. doi:10.1007/bf02699133. ISSN 0073-8301.
21. Birmingham, D; Blau, M.; Rakowski, M.; Thompson, G. (1991). "Topological field theory". Physics Reports. 209 (4–5): 129–340. Bibcode:1991PhR...209..129B. doi:10.1016/0370-1573(91)90117-5.
22. Witten, E. (1988-09-01). "Topological sigma models". Communications in Mathematical Physics. 118 (3): 411–449. Bibcode:1988CMaPh.118..411W. doi:10.1007/BF01466725. ISSN 0010-3616.
23. Baulieu, L.; Singer, I.M. (1988). "The topological sigma model". Communications in Mathematical Physics. 125 (2): 227–237. doi:10.1007/BF01217907.
24. Witten, E. (1988-09-01). "Topological quantum field theory". Communications in Mathematical Physics. 117 (3): 353–386. Bibcode:1988CMaPh.117..353W. doi:10.1007/BF01223371. ISSN 0010-3616.
25. Witten, E. (1982). "Supersymmetry and Morse theory". Journal of Differential Geometry. 17 (4): 661–692. doi:10.4310/jdg/1214437492. ISSN 0022-040X.
26. Labastida, J. M. F. (1989-12-01). "Morse theory interpretation of topological quantum field theories". Communications in Mathematical Physics. 123 (4): 641–658. Bibcode:1989CMaPh.123..641L. CiteSeerX 10.1.1.509.3123. doi:10.1007/BF01218589. ISSN 0010-3616.
27. Nicolai, H. (1980-12-22). "Supersymmetry and functional integration measures". Nuclear Physics B. 176 (2): 419–428. Bibcode:1980NuPhB.176..419N. doi:10.1016/0550-3213(80)90460-5.
28. Nicolai, H. (1980-01-28). "On a new characterization of scalar supersymmetric theories" (PDF). Physics Letters B. 89 (3): 341–346. Bibcode:1980PhLB...89..341N. doi:10.1016/0370-2693(80)90138-0.
29. Baulieu, L.; Grossman, B. (1988). "A topological interpretation of stochastic quantization". Physics Letters B. 212 (3): 351–356. doi:10.1016/0370-2693(88)91328-7.
30. Ovchinnikov, I.V. (2013-01-15). "Topological field theory of dynamical systems. II". Chaos: An Interdisciplinary Journal of Nonlinear Science. 23 (1): 013108. arXiv:1212.1989. Bibcode:2013Chaos..23a3108O. doi:10.1063/1.4775755. ISSN 1054-1500. PMID 23556945.
31. Graham, R. (1988). "Lyapunov Exponents and Supersymmetry of Stochastic Dynamical Systems". EPL. 5 (2): 101–106. Bibcode:1988EL......5..101G. doi:10.1209/0295-5075/5/2/002. ISSN 0295-5075.
32. Ovchinnikov, I.V.; Ensslin, T. A. (2016). "Kinematic dynamo, supersymmetry breaking, and chaos". Physical Review D. 93 (8): 085023. arXiv:1512.01651. Bibcode:2016PhRvD..93h5023O. doi:10.1103/PhysRevD.93.085023.
33. Ancona, A.; Elworthy, K. D.; Emery, M.; Kunita, H. (2013). Stochastic differential geometry at Saint-Flour. Springer. ISBN 9783642341700. OCLC 811000422.
34. Kunita, H. (1997). Stochastic flows and stochastic differential equations. Cambridge University Press. ISBN 978-0521599252. OCLC 36864963.
35. Slavík, A. (2013). "Generalized differential equations: Differentiability of solutions with respect to initial conditions and parameters". Journal of Mathematical Analysis and Applications. 402 (1): 261–274. doi:10.1016/j.jmaa.2013.01.027.
36. Gilmore, R.; Lefranc, M. (2011). The topology of chaos : Alice in stretch and squeezeland. Wiley-VCH. ISBN 9783527410675. OCLC 967841676.
37. Chung, D. J. H.; Everett, L. L.; Kane, G. L.; King, S. F.; Lykken, J.; Wang, Lian-Tao (2005-02-01). "The soft supersymmetry-breaking Lagrangian: theory and applications". Physics Reports. 407 (1–3): 1–203. arXiv:hep-ph/0312378. Bibcode:2005PhR...407....1C. doi:10.1016/j.physrep.2004.08.032.
38. Watkins, N. W.; Pruessner, G.; Chapman, S. C.; Crosby, N. B.; Jensen, H. J. (2016-01-01). "25 Years of Self-organized Criticality: Concepts and Controversies". Space Science Reviews. 198 (1–4): 3–44. arXiv:1504.04991. Bibcode:2016SSRv..198....3W. doi:10.1007/s11214-015-0155-x. ISSN 0038-6308.
39. Ovchinnikov, I. V. (2016-06-01). "Supersymmetric Theory of Stochastics: Demystification of Self-Organized Criticality". In Skiadas C.H. and Skiadas C. (ed.). Handbook of Applications of Chaos Theory. Chapman and Hall/CRC. pp. 271–305. doi:10.1201/b20232. ISBN 9781466590441.
40. Bak, P.; Tang, C.; Wiesenfeld, K. (1987). "Self-organized criticality: An explanation of the 1/f noise". Physical Review Letters. 59 (4): 381–384. Bibcode:1987PhRvL..59..381B. doi:10.1103/PhysRevLett.59.381. PMID 10035754.
41. Bouya, I.; Dormy, E. (2013-03-01). "Revisiting the ABC flow dynamo". Physics of Fluids. 25 (3): 037103–037103–10. arXiv:1206.5186. Bibcode:2013PhFl...25c7103B. doi:10.1063/1.4795546. ISSN 1070-6631.
42. Frenkel, E.; Losev, A.; Nekrasov, N. (2007). "Notes on instantons in topological field theory and beyond". Nuclear Physics B: Proceedings Supplements. 171: 215–230. arXiv:hep-th/0702137. Bibcode:2007NuPhS.171..215F. doi:10.1016/j.nuclphysbps.2007.06.013.
43. Di Ventra, M.; Traversa, F. L.; Ovchinnikov, I. V. (2017). "Topological Field Theory and Computing with Instantons". Annalen der Physik. 2017 (12): 1700123. arXiv:1609.03230. Bibcode:2017AnP...52900123D. doi:10.1002/andp.201700123. ISSN 1521-3889.