Stooge sort

Stooge sort is a recursive sorting algorithm. It is notable for its exceptionally bad time complexity of O(n^{log 3 / log 1.5} ) = O(n^2.7095...). The running time of the algorithm is thus slower compared to reasonable sorting algorithms, and is slower than Bubble sort, a canonical example of a fairly inefficient sort. It is however more efficient than Slowsort. The name comes from The Three Stooges.[1]

Stooge sort

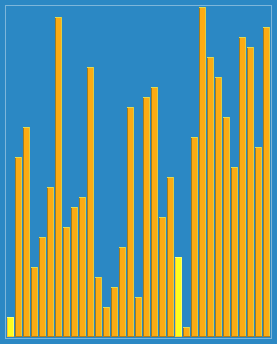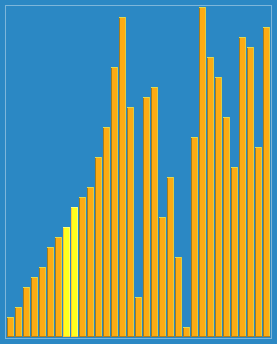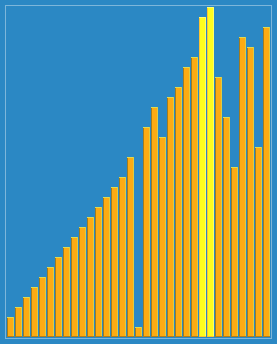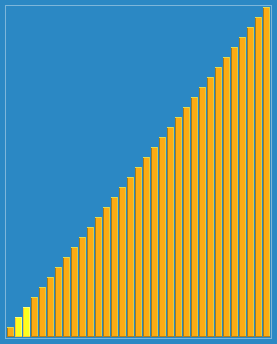Visualization of Stooge sort (only shows swaps).
Class	Sorting algorithm
Data structure	Array
Worst-case performance	O(n^log 3/log 1.5)
Worst-case space complexity	O(n)

The algorithm is defined as follows:

• If the value at the start is larger than the value at the end, swap them.
• If there are 3 or more elements in the list, then:
  • Stooge sort the initial 2/3 of the list
  • Stooge sort the final 2/3 of the list
  • Stooge sort the initial 2/3 of the list again

It is important to get the integer sort size used in the recursive calls by rounding the 2/3 upwards, e.g. rounding 2/3 of 5 should give 4 rather than 3, as otherwise the sort can fail on certain data.

Implementation

 function stoogesort(array L, i = 0, j = length(L)-1){
     if L[i] > L[j] then
         L[i] ↔ L[j]
     if (j - i + 1) > 2 then
         t = (j - i + 1) / 3
         stoogesort(L, i  , j-t)
         stoogesort(L, i+t, j  )
         stoogesort(L, i  , j-t)
     return L
 }

References

1. https://courses.cs.washington.edu/courses/cse373/13wi/lectures/02-22/18-sorting1-bogo-stooge-bubble.pdf

• Black, Paul E. "stooge sort". Dictionary of Algorithms and Data Structures. National Institute of Standards and Technology. Retrieved 18 June 2011.
• Cormen, Thomas H.; Leiserson, Charles E.; Rivest, Ronald L.; Stein, Clifford (2001) [1990]. "Problem 7-3". Introduction to Algorithms (2nd ed.). MIT Press and McGraw-Hill. pp. 161–162. ISBN 0-262-03293-7.

External links

• Sorting Algorithms (including Stooge sort)
• Stooge sort – implementation and comparison