Sphere packing in a sphere
Sphere packing in a sphere is a three-dimensional packing problem with the objective of packing a given number of equal spheres inside a unit sphere. It is the three-dimensional equivalent of the circle packing in a circle problem in two dimensions.
| Number of inner spheres |
Maximum radius of inner spheres[1] | Packing density |
Optimality | Diagram | |
|---|---|---|---|---|---|
| Exact form | Approximate | ||||
| 1 | 1.0000 | 1 | Trivially optimal. |  | |
| 2 | 0.5000 | 0.25 | Trivially optimal. | 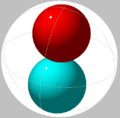 | |
| 3 | 0.4641... | 0.29988... | Trivially optimal. | 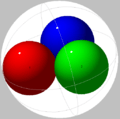 | |
| 4 | 0.4494... | 0.36326... | Proven optimal. |  | |
| 5 | 0.4142... | 0.35533... | Proven optimal. |  | |
| 6 | 0.4142... | 0.42640... | Proven optimal. |  | |
| 7 | 0.3859... | 0.40231... | Proven optimal. |  | |
| 8 | 0.3780... | 0.43217... | Proven optimal. |  | |
| 9 | 0.3660... | 0.44134... | Proven optimal. |  | |
| 10 | 0.3530... | 0.44005... | Proven optimal. |  | |
| 11 | 0.3445... | 0.45003... | Proven optimal. |  | |
| 12 | 0.3445... | 0.49095... | Proven optimal. |  | |
References
- Pfoertner, Hugo (2008-02-02). "Densest Packings of n Equal Spheres in a Sphere of Radius 1. Largest Possible Radii". Archived from the original on 2012-03-30. Retrieved 2013-11-02.
- Huang, WenQi; Yu, Liang (2012). "Serial Symmetrical Relocation Algorithm for the Equal Sphere Packing Problem". arXiv:1202.4149.
- Gensane, T. (2003). "Dense packings of equal spheres in a larger sphere". Les Cahiers du LMPA J. Liouville. 188.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.