Circle packing in a square
Circle packing in a square is a packing problem in applied mathematics, where the aim is to pack n unit circles into the smallest possible square; or, equivalently, to arrange n points in a unit square aiming to get the greatest minimal separation, dn, between points.[1] To convert between these two formulations of the problem, the square side for unit circles will be .
Solutions (not necessarily optimal) have been computed for every N≤10,000.[2] Solutions up to N=20 are shown below:[2]
| Number of circles (n) | Square size (side length (L)) | dn[1] | Number density (n/L^2) | Figure |
|---|---|---|---|---|
| 1 | 2 | ∞ | 0.25 | |
| 2 | ≈ 3.414... |
≈ 1.414... |
0.172... | 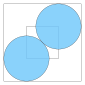 |
| 3 | ≈ 3.931... |
≈ 1.035... |
0.194... | 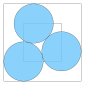 |
| 4 | 4 | 1 | 0.25 | 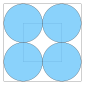 |
| 5 | ≈ 4.828... |
≈ 0.707... |
0.215... | 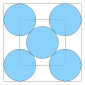 |
| 6 | ≈ 5.328... |
≈ 0.601... |
0.211... | 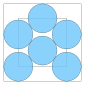 |
| 7 | ≈ 5.732... |
≈ 0.536... |
0.213... | 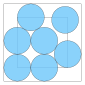 |
| 8 | ≈ 5.863... |
≈ 0.518... |
0.233... | 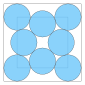 |
| 9 | 6 | 0.5 | 0.25 | 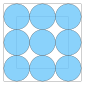 |
| 10 | 6.747... | 0.421... OEIS: A281065 | 0.220... | 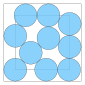 |
| 11 | 7.022... | 0.398... | 0.223... | 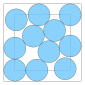 |
| 12 | ≈ 7.144... |
0.389... | 0.235... | 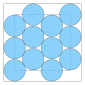 |
| 13 | 7.463... | 0.366... | 0.233... | 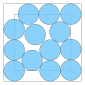 |
| 14 | ≈ 7.732... |
0.348... | 0.226... |  |
| 15 | ≈ 7.863... |
0.341... | 0.243... | 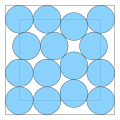 |
| 16 | 8 | 0.333... | 0.25 |  |
| 17 | 8.532... | 0.306... | 0.234... | 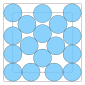 |
| 18 | ≈ 8.656... |
0.300... | 0.240... | 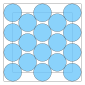 |
| 19 | 8.907... | 0.290... | 0.240... |  |
| 20 | ≈ 8.978... |
0.287... | 0.248... | 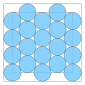 |
The obvious square packing is optimal for 1, 4, 9, 16, 25, and 36 circles (the smallest six square numbers), but ceases to be optimal for larger squares from 49 onwards.[2]
References
- Croft, Hallard T.; Falconer, Kenneth J.; Guy, Richard K. (1991). Unsolved Problems in Geometry. New York: Springer-Verlag. pp. 108–110. ISBN 0-387-97506-3.
- Eckard Specht (20 May 2010). "The best known packings of equal circles in a square". Retrieved 25 May 2010.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.