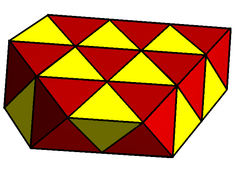
Snub (geometry)

In geometry, a snub is an operation applied to a polyhedron. The term originates from Kepler's names of two Archimedean solids, for the snub cube (cubus simus) and snub dodecahedron (dodecaedron simum).[1] In general, snubs have chiral symmetry with two forms, with clockwise or counterclockwise orientations. By Kepler's names, a snub can be seen as an expansion of a regular polyhedron, with the faces moved apart, and twists on their centers, adding new polygons centered on the original vertices, and pairs of triangles fitting between the original edges.

The two snubbed Archimedean solids

Snub cube or Snub cuboctahedron

Snub dodecahedron or Snub icosidodecahedron

Two chiral copies of the snub cube, as alternated (red or green) vertices of the truncated cuboctahedron.

A snub cube can be constructed from a transformed rhombicuboctahedron by rotating the 6 blue square faces until the 12 white square become pairs of equilateral triangles.

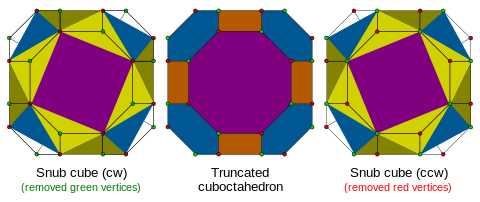
The terminology was generalized by Coxeter, with a slightly different definition, for a wider set of uniform polytopes.

Conway snubs

John Conway explored generalized polyhedron operators, defining what is now called Conway polyhedron notation, which can be applied to polyhedra and tilings. Conway calls Coxeter's operation a semi-snub.[2]

In this notation, snub is defined by the dual and gyro operators, as s = dg, and it is equivalent to an alternation of a truncation of an ambo operator. Conway's notation itself avoids Coxeter's alternation (half) operation since it only applies for polyhedra with only even-sided faces.

Snubbed regular figures

Form	Polyhedra			Euclidean		Hyperbolic
Conway notation	sT	sC = sO	sI = sD	sQ	sH = sΔ	sΔ7
Snubbed polyhedra	Tetrahedron	Cube or octahedron	Icosahedron or dodecahedron	Square tiling	Hexagonal tiling or Triangular tiling	Heptagonal tiling or Order-7 triangular tiling
Image

In 4-dimensions, Conway suggests the snub 24-cell should be called a semi-snub 24-cell because it doesn't represent an alternated omnitruncated 24-cell like his 3-dimensional polyhedron usage. It is instead actually an alternated truncated 24-cell.[3]

Coxeter's snubs, regular and quasiregular

Snub cube, derived from cube or cuboctahedron

Seed	Rectified r	Truncated t	Alternated h
Cube	Cuboctahedron Rectified cube	Truncated cuboctahedron Cantitruncated cube	Snub cuboctahedron Snub rectified cube
C	CO rC	tCO trC or trO	htCO = sCO htrC = srC
{4,3}	${\displaystyle {\begin{Bmatrix}4\\3\end{Bmatrix}}}$ or r{4,3}	${\displaystyle t{\begin{Bmatrix}4\\3\end{Bmatrix}}}$ or tr{4,3}	${\displaystyle ht{\begin{Bmatrix}4\\3\end{Bmatrix}}=s{\begin{Bmatrix}4\\3\end{Bmatrix}}}$ htr{4,3} = sr{4,3}
	or	or	or

Coxeter's snub terminology is slightly different, meaning an alternated truncation, deriving the snub cube as a snub cuboctahedron, and the snub dodecahedron as a snub icosidodecahedron. This definition is used in the naming two Johnson solids: snub disphenoid, and snub square antiprism, as well as higher dimensional polytopes such as the 4-dimensional snub 24-cell, or s{3,4,3}.

A regular polyhedron (or tiling) with Schläfli symbol, ${\displaystyle {\begin{Bmatrix}p,q\end{Bmatrix}}}$, and Coxeter diagram , has truncation defined as ${\displaystyle t{\begin{Bmatrix}p,q\end{Bmatrix}}}$, and and snub defined as an alternated truncation ${\displaystyle ht{\begin{Bmatrix}p,q\end{Bmatrix}}=s{\begin{Bmatrix}p,q\end{Bmatrix}}}$, and Coxeter diagram . This construction requires q to be even.

A quasiregular polyhedron ${\displaystyle {\begin{Bmatrix}p\\q\end{Bmatrix}}}$ or r{p,q}, with Coxeter diagram or has a quasiregular truncation defined as ${\displaystyle t{\begin{Bmatrix}p\\q\end{Bmatrix}}}$ or tr{p,q}, and Coxeter diagram or and quasiregular snub defined as an alternated truncated rectification ${\displaystyle ht{\begin{Bmatrix}p\\q\end{Bmatrix}}=s{\begin{Bmatrix}p\\q\end{Bmatrix}}}$ or htr{p,q} = sr{p,q}, and Coxeter diagram or .

For example, Kepler's snub cube is derived from the quasiregular cuboctahedron, with a vertical Schläfli symbol ${\displaystyle {\begin{Bmatrix}4\\3\end{Bmatrix}}}$, and Coxeter diagram , and so is more explicitly called a snub cuboctahedron, expressed by a vertical Schläfli symbol ${\displaystyle s{\begin{Bmatrix}4\\3\end{Bmatrix}}}$ and Coxeter diagram . The snub cuboctahedron is the alternation of the truncated cuboctahedron, ${\displaystyle t{\begin{Bmatrix}4\\3\end{Bmatrix}}}$ and .

Regular polyhedra with even-order vertices to also be snubbed as alternated truncation, like a snub octahedron, ${\displaystyle s{\begin{Bmatrix}3,4\end{Bmatrix}}}$, (and snub tetratetrahedron, as ${\displaystyle s{\begin{Bmatrix}3\\3\end{Bmatrix}}}$, ) represents the pseudoicosahedron, a regular icosahedron with pyritohedral symmetry. The snub octahedron is the alternation of the truncated octahedron, ${\displaystyle t{\begin{Bmatrix}3,4\end{Bmatrix}}}$ and , or tetrahedral symmetry form: ${\displaystyle t{\begin{Bmatrix}3\\3\end{Bmatrix}}}$ and .

Seed	Truncated t	Alternated h
Octahedron O	Truncated octahedron tO	Snub octahedron htO or sO
{3,4}	t{3,4}	ht{3,4} = s{3,4}

Coxeter's snub operation also allows n-antiprisms to be defined as ${\displaystyle s{\begin{Bmatrix}2\\n\end{Bmatrix}}}$ or ${\displaystyle s{\begin{Bmatrix}2,2n\end{Bmatrix}}}$, based on n-prisms ${\displaystyle t{\begin{Bmatrix}2\\n\end{Bmatrix}}}$ or ${\displaystyle t{\begin{Bmatrix}2,2n\end{Bmatrix}}}$, while ${\displaystyle {\begin{Bmatrix}2,n\end{Bmatrix}}}$ is a regular n-hosohedron, a degenerate polyhedron, but a valid tiling on the sphere with digon or lune-shaped faces.

Snub hosohedra, {2,2p}

Image
Coxeter diagrams							... ...
Schläfli symbols	s{2,4}	s{2,6}	s{2,8}	s{2,10}	s{2,12}	s{2,14}	s{2,16}...	s{2,∞}
	sr{2,2} ${\displaystyle s{\begin{Bmatrix}2\\2\end{Bmatrix}}}$	sr{2,3} ${\displaystyle s{\begin{Bmatrix}2\\3\end{Bmatrix}}}$	sr{2,4} ${\displaystyle s{\begin{Bmatrix}2\\4\end{Bmatrix}}}$	sr{2,5} ${\displaystyle s{\begin{Bmatrix}2\\5\end{Bmatrix}}}$	sr{2,6} ${\displaystyle s{\begin{Bmatrix}2\\6\end{Bmatrix}}}$	sr{2,7} ${\displaystyle s{\begin{Bmatrix}2\\7\end{Bmatrix}}}$	sr{2,8}... ${\displaystyle s{\begin{Bmatrix}2\\8\end{Bmatrix}}}$...	sr{2,∞} ${\displaystyle s{\begin{Bmatrix}2\\\infty \end{Bmatrix}}}$
Conway notation	A2 = T	A3 = O	A4	A5	A6	A7	A8...	A∞

The same process applies for snub tilings:

Triangular tiling Δ	Truncated triangular tiling tΔ	Snub triangular tiling htΔ = sΔ
{3,6}	t{3,6}	ht{3,6} = s{3,6}

Examples

Snubs based on {p,4}

Space	Spherical		Euclidean	Hyperbolic
Image
Coxeter diagram								...
Schläfli symbol	s{2,4}	s{3,4}	s{4,4}	s{5,4}	s{6,4}	s{7,4}	s{8,4}	...s{∞,4}

Quasiregular snubs based on r{p,3}

Conway notation	Spherical				Euclidean	Hyperbolic
Image
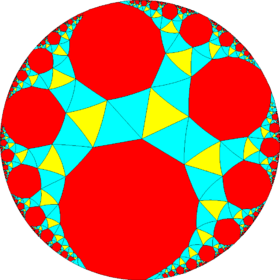Coxeter diagram								...
Schläfli symbol	sr{2,3}	sr{3,3}	sr{4,3}	sr{5,3}	sr{6,3}	sr{7,3}	sr{8,3}	...sr{∞,3}
	${\displaystyle s{\begin{Bmatrix}2\\3\end{Bmatrix}}}$	${\displaystyle s{\begin{Bmatrix}3\\3\end{Bmatrix}}}$	${\displaystyle s{\begin{Bmatrix}4\\3\end{Bmatrix}}}$	${\displaystyle s{\begin{Bmatrix}5\\3\end{Bmatrix}}}$	${\displaystyle s{\begin{Bmatrix}6\\3\end{Bmatrix}}}$	${\displaystyle s{\begin{Bmatrix}7\\3\end{Bmatrix}}}$	${\displaystyle s{\begin{Bmatrix}8\\3\end{Bmatrix}}}$	${\displaystyle s{\begin{Bmatrix}\infty \\3\end{Bmatrix}}}$
Conway notation	A3	sT	sC or sO	sD or sI	sΗ or sΔ

Quasiregular snubs based on r{p,4}

Space	Spherical		Euclidean	Hyperbolic
Image
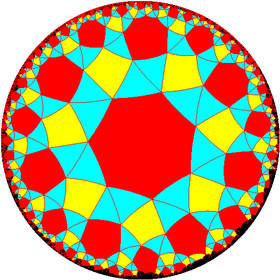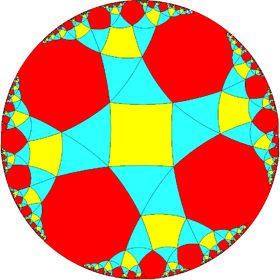Coxeter diagram								...
Schläfli symbol	sr{2,4}	sr{3,4}	sr{4,4}	sr{5,4}	sr{6,4}	sr{7,4}	sr{8,4}	...sr{∞,4}
	${\displaystyle s{\begin{Bmatrix}2\\4\end{Bmatrix}}}$	${\displaystyle s{\begin{Bmatrix}3\\4\end{Bmatrix}}}$	${\displaystyle s{\begin{Bmatrix}4\\4\end{Bmatrix}}}$	${\displaystyle s{\begin{Bmatrix}5\\4\end{Bmatrix}}}$	${\displaystyle s{\begin{Bmatrix}6\\4\end{Bmatrix}}}$	${\displaystyle s{\begin{Bmatrix}7\\4\end{Bmatrix}}}$	${\displaystyle s{\begin{Bmatrix}8\\4\end{Bmatrix}}}$	${\displaystyle s{\begin{Bmatrix}\infty \\4\end{Bmatrix}}}$
Conway notation	A4	sC or sO	sQ

Nonuniform snub polyhedra

Nonuniform polyhedra with all even-valance vertices can be snubbed, including some infinite sets, for example:

Snub bipyramids sdt{2,p}

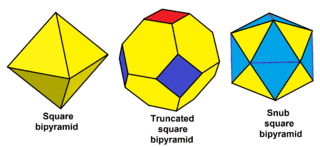Snub square bipyramid
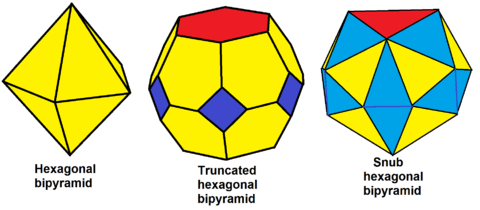Snub hexagonal bipyramid

Snub rectified bipyramids srdt{2,p}

Snub antiprisms s{2,2p}

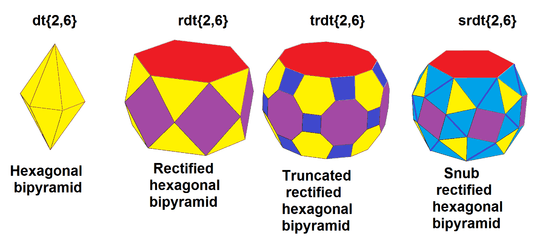Image				...
Schläfli symbols	ss{2,4}	ss{2,6}	ss{2,8}	ss{2,10}...
	ssr{2,2} ${\displaystyle ss{\begin{Bmatrix}2\\2\end{Bmatrix}}}$	ssr{2,3} ${\displaystyle ss{\begin{Bmatrix}2\\3\end{Bmatrix}}}$	ssr{2,4} ${\displaystyle ss{\begin{Bmatrix}2\\4\end{Bmatrix}}}$	ssr{2,5}... ${\displaystyle ss{\begin{Bmatrix}2\\5\end{Bmatrix}}}$

Coxeter's uniform snub star-polyhedra

Snub star-polyhedra are constructed by their Schwarz triangle (p q r), with rational ordered mirror-angles, and all mirrors active and alternated.

Snubbed uniform star-polyhedra

s{3/2,3/2}	s{(3,3,5/2)}	sr{5,5/2}	s{(3,5,5/3)}	sr{5/2,3}
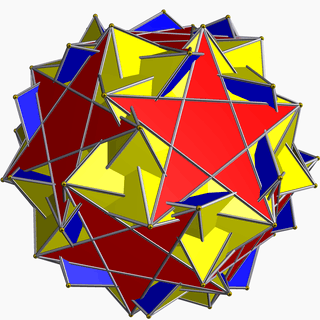sr{5/3,5}	s{(5/2,5/3,3)}	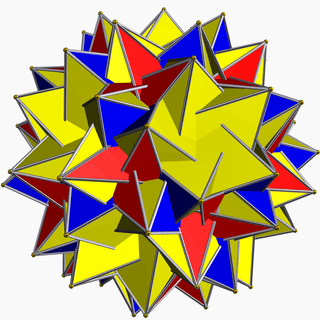sr{5/3,3}	s{(3/2,3/2,5/2)}	s{3/2,5/3}

Coxeter's higher-dimensional snubbed polytopes and honeycombs

In general, a regular polychoron with Schläfli symbol, ${\displaystyle {\begin{Bmatrix}p,q,r\end{Bmatrix}}}$, and Coxeter diagram , has a snub with extended Schläfli symbol ${\displaystyle s{\begin{Bmatrix}p,q,r\end{Bmatrix}}}$, and .

A rectified polychoron ${\displaystyle {\begin{Bmatrix}p\\q,r\end{Bmatrix}}}$ = r{p,q,r}, and has snub symbol ${\displaystyle s{\begin{Bmatrix}p\\q,r\end{Bmatrix}}}$ = sr{p,q,r}, and .

Examples

Orthogonal projection of snub 24-cell

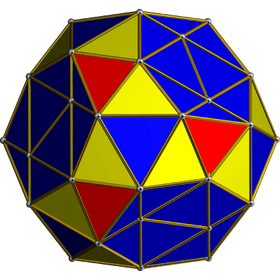
There is only one uniform convex snub in 4-dimensions, the snub 24-cell. The regular 24-cell has Schläfli symbol, ${\displaystyle {\begin{Bmatrix}3,4,3\end{Bmatrix}}}$, and Coxeter diagram , and the snub 24-cell is represented by ${\displaystyle s{\begin{Bmatrix}3,4,3\end{Bmatrix}}}$, Coxeter diagram . It also has an index 6 lower symmetry constructions as ${\displaystyle s\left\{{\begin{array}{l}3\\3\\3\end{array}}\right\}}$ or s{3^1,1,1} and , and an index 3 subsymmetry as ${\displaystyle s{\begin{Bmatrix}3\\3,4\end{Bmatrix}}}$ or sr{3,3,4}, and or .

The related snub 24-cell honeycomb can be seen as a ${\displaystyle s{\begin{Bmatrix}3,4,3,3\end{Bmatrix}}}$ or s{3,4,3,3}, and , and lower symmetry ${\displaystyle s{\begin{Bmatrix}3\\3,4,3\end{Bmatrix}}}$ or sr{3,3,4,3} and or , and lowest symmetry form as ${\displaystyle s\left\{{\begin{array}{l}3\\3\\3\\3\end{array}}\right\}}$ or s{3^1,1,1,1} and .

A Euclidean honeycomb is an alternated hexagonal slab honeycomb, s{2,6,3}, and or sr{2,3,6}, and or sr{2,3^[3]}, and .

Another Euclidean (scaliform) honeycomb is an alternated square slab honeycomb, s{2,4,4}, and or sr{2,4^1,1} and :

The only uniform snub hyperbolic uniform honeycomb is the snub hexagonal tiling honeycomb, as s{3,6,3} and , which can also be constructed as an alternated hexagonal tiling honeycomb, h{6,3,3}, . It is also constructed as s{3^[3,3]} and .

Another hyperbolic (scaliform) honeycomb is a snub order-4 octahedral honeycomb, s{3,4,4}, and .

See also

• Snub polyhedron

Polyhedron operators

Seed	Truncation	Rectification	Bitruncation	Dual	Expansion	Omnitruncation	Alternations
t0{p,q} {p,q}	t01{p,q} t{p,q}	t1{p,q} r{p,q}	t12{p,q} 2t{p,q}	t2{p,q} 2r{p,q}	t02{p,q} rr{p,q}	t012{p,q} tr{p,q}	ht0{p,q} h{q,p}	ht12{p,q} s{q,p}	ht012{p,q} sr{p,q}

References

1. Kepler, Harmonices Mundi, 1619
2. Conway, (2008) p.287 Coxeter's semi-snub operation
3. Conway, 2008, p.401 Gosset's Semi-snub Polyoctahedron

• Coxeter, Harold Scott MacDonald; Longuet-Higgins, M. S.; Miller, J. C. P. (1954). "Uniform polyhedra". Philosophical Transactions of the Royal Society of London. Series A. Mathematical and Physical Sciences. The Royal Society. 246 (916): 401–450. Bibcode:1954RSPTA.246..401C. doi:10.1098/rsta.1954.0003. ISSN 0080-4614. JSTOR 91532. MR 0062446.CS1 maint: ref=harv (link)
• Coxeter, H.S.M. Regular Polytopes, (3rd edition, 1973), Dover edition, ISBN 0-486-61480-8 (pp. 154–156 8.6 Partial truncation, or alternation)
• Kaleidoscopes: Selected Writings of H.S.M. Coxeter, edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6 , Googlebooks
  • (Paper 17) Coxeter, The Evolution of Coxeter–Dynkin diagrams, [Nieuw Archief voor Wiskunde 9 (1991) 233–248]
  • (Paper 22) H.S.M. Coxeter, Regular and Semi Regular Polytopes I, [Math. Zeit. 46 (1940) 380–407, MR 2,10]
  • (Paper 23) H.S.M. Coxeter, Regular and Semi-Regular Polytopes II, [Math. Zeit. 188 (1985) 559–591]
  • (Paper 24) H.S.M. Coxeter, Regular and Semi-Regular Polytopes III, [Math. Zeit. 200 (1988) 3–45]
• Coxeter, The Beauty of Geometry: Twelve Essays, Dover Publications, 1999, ISBN 978-0-486-40919-1 (Chapter 3: Wythoff's Construction for Uniform Polytopes)
• Norman Johnson Uniform Polytopes, Manuscript (1991)
  • N.W. Johnson: The Theory of Uniform Polytopes and Honeycombs, Ph.D. Dissertation, University of Toronto, 1966
• John H. Conway, Heidi Burgiel, Chaim Goodman-Strass, The Symmetries of Things 2008, ISBN 978-1-56881-220-5
• Weisstein, Eric W. "Snubification". MathWorld.
• Richard Klitzing, Snubs, alternated facetings, and Stott–Coxeter–Dynkin diagrams, Symmetry: Culture and Science, Vol. 21, No.4, 329–344, (2010)