Small complex rhombicosidodecahedron

In geometry, the small complex rhombicosidodecahedron (also known as the small complex ditrigonal rhombicosidodecahedron) is a degenerate uniform star polyhedron. It has 62 faces (20 triangles, 12 pentagrams and 30 squares), 120 (doubled) edges and 20 vertices. All edges are doubled (making it degenerate), sharing 4 faces, but are considered as two overlapping edges as a topological polyhedron.

Small complex rhombicosidodecahedron
Type	Uniform star polyhedron
Elements	F = 62, E = 120 (60x2) V = 20 (χ = -38)
Faces by sides	20{3}+12{5/2}+30{4}
Wythoff symbol	5/2 3 | 2
Symmetry group	Ih, [5,3], *532
Index references	U-, C-, W-
Dual polyhedron	Small complex rhombicosidodecacron
Vertex figure	3(3.4.5/2.4)
Bowers acronym	Sicdatrid

It can be constructed from the vertex figure 3(⁵/₂.4.3.4), thus making it also a cantellated great icosahedron. The "3" in front of this vertex figure indicates that each vertex in this degenerate polyhedron is in fact three coincident vertices. It may also be given the Schläfli symbol rr{​⁵⁄₂,3} or t_0,2{​⁵⁄₂,3}.

As a compound

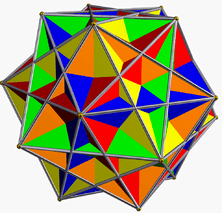
It can be seen as a compound of the small ditrigonal icosidodecahedron, U₃₀, and the compound of five cubes. It is also a facetting of the dodecahedron.

Compound polyhedron

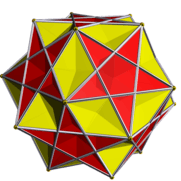Small ditrigonal icosidodecahedron	Compound of five cubes	Compound

As a cantellation

It can also be seen as a cantellation of the great icosahedron (or, equivalently, of the great stellated dodecahedron).

(p q 2)	Fund. triangle	Parent	Truncated	Rectified	Bitruncated	Birectified (dual)	Cantellated	Omnitruncated (Cantitruncated)	Snub
Wythoff symbol		q | p 2	2 q | p	2 | p q	2 p | q	p | q 2	p q | 2	p q 2 |	| p q 2
Schläfli symbol		t0{p,q}	t0,1{p,q}	t1{p,q}	t1,2{p,q}	t2{p,q}	t0,2{p,q}	t0,1,2{p,q}	s{p,q}
Coxeter–Dynkin diagram
Vertex figure		p^q	q.2p.2p	p.q.p.q	p.2q.2q	q^p	p.4.q.4	4.2p.2q	3.3.p.3.q
Icosahedral (​^5⁄2 3 2)		{3,​^5⁄2}	​^5⁄2.6.6	(3.​^5⁄2)^2	3.​^10⁄2.​^10⁄2	{​^5⁄2,3}	3.4.​^5⁄2.4	4.​^10⁄2.6	3.3.3.3.​^5⁄2

Related degenerate uniform polyhedra

Two other degenerate uniform polyhedra are also facettings of the dodecahedron. They are the complex rhombidodecadodecahedron (a compound of the ditrigonal dodecadodecahedron and the compound of five cubes) with vertex figure (​⁵⁄₃.4.5.4)/3 and the great complex rhombicosidodecahedron (a compound of the great ditrigonal icosidodecahedron and the compound of five cubes) with vertex figure (​⁵⁄₄.4.​³⁄₂.4)/3. All three degenerate uniform polyhedra have each vertex in fact being three coincident vertices and each edge in fact being two coincident edges.

They can all be constructed by cantellating regular polyhedra. The complex rhombidodecadodecahedron may be given the Schläfli symbol rr{​⁵⁄₃,5} or t_0,2{​⁵⁄₃,5}, while the great complex rhombicosidodecahedron may be given the Schläfli symbol rr{​⁵⁄₄,​³⁄₂} or t_0,2{​⁵⁄₄,​³⁄₂}.

Cantellated polyhedron	Small complex rhombicosidodecahedron		Complex rhombidodecadodecahedron		Great complex rhombicosidodecahedron
Related polyhedron	Great icosahedron	Great stellated dodecahedron	Great dodecahedron	Small stellated dodecahedron	Regular dodecahedron	Regular icosahedron

See also

• Small complex icosidodecahedron
• Great complex icosidodecahedron
• Complex rhombidodecadodecahedron
• Great complex rhombicosidodecahedron

References

• Klitzing, Richard. "3D uniform polyhedra sicdatrid".
• Klitzing, Richard. "3D uniform polyhedra cadditradid".
• Klitzing, Richard. "3D uniform polyhedra gicdatrid".