Septimal whole tone

In music, the septimal whole tone, septimal major second,[2] or supermajor second[3][4] play  is the musical interval exactly or approximately equal to an 8/7 ratio of frequencies.[5] It is about 231 cents wide in just intonation.[6] Although 24 equal temperament does not match this interval particularly well, its nearest representation is at 250 cents, approximately 19 cents sharp. The septimal whole tone may be derived from the harmonic series as the interval between the seventh and eighth harmonics and the term septimal refers to the fact that it utilizes the seventh harmonic.[6] It can also be thought of as the octave inversion of the 7/4 interval, the harmonic seventh.

Origin of large and small seconds and thirds in harmonic series.[7]
septimal major second
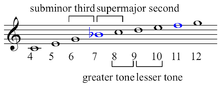
Inverseharmonic seventh
Name
Other namesSeptimal whole tone, Supermajor second
AbbreviationS2, SM2
Size
Semitones~2.5
Interval class~2.5
Just interval8:7[1]
Cents
Equal temperament200
24 equal temperament250
Just intonation231
3-limit 9:8 major tone Play .
7-limit 8:7 septimal whole tone Play .
Septimal major second on B7♭ Play .

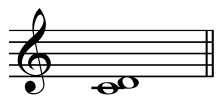
No close approximation to this interval exists in the standard 12 equal temperament used in most modern western music. The very simple 5 equal temperament is the smallest system to match this interval well. 26 equal temperament matches this interval almost perfectly with an error of only 0.4 cents, but at the cost of the significant flatness of its major thirds and fifths. 31 equal temperament, which has much more accurate fifths and major thirds, approximates 8/7 with a slightly higher error of 1.1 cents.

Sources
  1. Haluska, Jan (2003). The Mathematical Theory of Tone Systems, p.xxiii. ISBN 0-8247-4714-3. Septimal whole tone.
  2. Partch, Harry (1979). Genesis of a Music, p.68. ISBN 0-306-80106-X.
  3. Royal Society (Great Britain) (1880, digitized Feb 26, 2008). Proceedings of the Royal Society of London, Volume 30, p.531. Harvard University.
  4. Society of Arts (Great Britain) (1877, digitized Nov 19, 2009). Journal of the Society of Arts, Volume 25, p.670. The Society.
  5. Andrew Horner, Lydia Ayres (2002). Cooking with Csound: Woodwind and Brass Recipes, p.131. ISBN 0-89579-507-8. "Super-Major Second".
  6. Leta E. Miller, Fredric Lieberman (2006). Lou Harrison, p.72. ISBN 0-252-03120-2.
  7. Leta E. Miller, ed. (1988). Lou Harrison: Selected keyboard and chamber music, 1937-1994, p.xliii. ISBN 978-0-89579-414-7.
gollark: ++remind "august 2" replace military with swarms of bees
gollark: It parses "july 1"? How highly advanced.
gollark: Huh, wow.
gollark: ++remind 9mo2w2d something something lyric/gnobody bet?
gollark: +>auction
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.