Separable permutation

In combinatorial mathematics, a separable permutation is a permutation that can be obtained from the trivial permutation 1 by direct sums and skew sums.[1] Separable permutations may be characterized by the forbidden permutation patterns 2413 and 3142;[2] they are also the permutations whose permutation graphs are cographs and the permutations that realize the series-parallel partial orders. It is possible to test in polynomial time whether a given separable permutation is a pattern in a larger permutation, or to find the longest common subpattern of two separable permutations.

Block structuring of the (transposed) permutation matrix of the separable permutation (4,5,2,1,3,8,6,7) and corresponding labeled binary tree; colors indicate depth in the tree

Definition and characterization
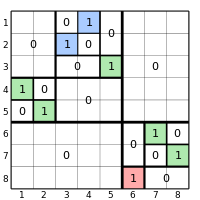
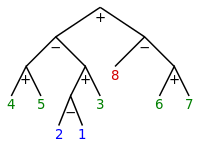
A large typical separable permutation

Bose, Buss & Lubiw (1998) define a separable permutation to be a permutation that has a separating tree: a rooted binary tree in which the elements of the permutation appear (in permutation order) at the leaves of the tree, and in which the descendants of each tree node form a contiguous subset of these elements. Each interior node of the tree is either a positive node in which all descendants of the left child are smaller than all descendants of the right node, or a negative node in which all descendants of the left node are greater than all descendants of the right node. There may be more than one tree for a given permutation: if two nodes that are adjacent in the same tree have the same sign, then they may be replaced by a different pair of nodes using a tree rotation operation.

Each subtree of a separating tree may be interpreted as itself representing a smaller separable permutation, whose element values are determined by the shape and sign pattern of the subtree. A one-node tree represents the trivial permutation, a tree whose root node is positive represents the direct sum of permutations given by its two child subtrees, and a tree whose root node is negative represents the skew sum of the permutations given by its two child subtrees. In this way, a separating tree is equivalent to a construction of the permutation by direct and skew sums, starting from the trivial permutation.

As Bose, Buss & Lubiw (1998) prove, separable permutations may also be characterized in terms of permutation patterns: a permutation is separable if and only if it contains neither 2413 nor 3142 as a pattern.[2]

The separable permutations also have a characterization from algebraic geometry: if a collection of distinct real polynomials all have equal values at some number x, then the permutation that describes how the numerical ordering of the polynomials changes at x is separable, and every separable permutation can be realized in this way.[3]

Combinatorial enumeration

The separable permutations are enumerated by the Schröder numbers. That is, there is one separable permutation of length one, two of length two, and in general the number of separable permutations of a given length (starting with length one) is

1, 2, 6, 22, 90, 394, 1806, 8558, .... (sequence A006318 in the OEIS)

This result was proven for a class of permutation matrices equivalent to the separable permutations by Shapiro & Stephens (1991), by using a canonical form of the separating tree in which the right child of each node has a different sign than the node itself and then applying the theory of generating functions to these trees. Another proof applying more directly to separable permutations themselves, was given by West (1995).[4]

Algorithms

Bose, Buss & Lubiw (1998) showed that it is possible to determine in polynomial time whether a given separable permutation is a pattern in a larger permutation, in contrast to the same problem for non-separable permutations, which is NP-complete.

The problem of finding the longest separable pattern that is common to a set of input permutations may be solved in polynomial time for a fixed number of input permutations, but is NP-hard when the number of input permutations may be variable, and remains NP-hard even when the inputs are all themselves separable.[5]

History

Separable permutations first arose in the work of Avis & Newborn (1981), who showed that they are precisely the permutations which can be sorted by an arbitrary number of pop-stacks in series, where a pop-stack is a restricted form of stack in which any pop operation pops all items at once.

Shapiro & Stephens (1991) considered separable permutations again in their study of bootstrap percolation, a process in which an initial permutation matrix is modified by repeatedly changing to one any matrix coefficient that has two or more orthogonal neighbors equal to one. As they show, the class of permutations that are transformed by this process into the all-one matrix is exactly the class of separable permutations.

The term "separable permutation" was introduced later by Bose, Buss & Lubiw (1998), who considered them for their algorithmic properties.

The separable permutation 43512 and its corresponding permutation graph

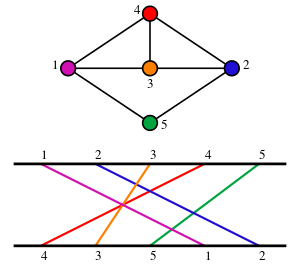
Every permutation can be used to define a permutation graph, a graph whose vertices are the elements of the permutation and whose edges are the inversions of the permutation. In the case of a separable permutation, the structure of this graph can be read off from the separation tree of the permutation: two vertices of the graph are adjacent if and only if their lowest common ancestor in the separation tree is negative. The graphs that can be formed from trees in this way are called cographs (short for complement-reducible graphs) and the trees from which they are formed are called cotrees. Thus, the separable permutations are exactly the permutations whose permutation graphs are cographs.[6] The forbidden graph characterization of the cographs (they are the graphs with no four-vertex induced path) corresponds to the two four-element forbidden patterns of the separable permutations.

Separable permutations also closely related to series-parallel partial orders, the partially ordered sets whose comparability graphs are the cographs. As with the cographs and separable permutations, the series-parallel partial orders may also be characterized by four-element forbidden suborders. Every permutation defines a partial order whose order dimension is two, in which the elements to be ordered are the elements of the permutation, and in which x ≤ y whenever x has a smaller numerical value than y and is left of it in the permutation. The permutations for which this partial order is series-parallel are exactly the separable permutations.

Separable permutations may also be used to describe hierarchical partitions of rectangles into smaller rectangles (so-called "slicing floorplans", used for instance in the design of integrated circuits) by using the positive and negative signs of the separating tree to describe horizontal and vertical slices of a rectangle into smaller rectangles.[7]

The separable permutations include as a special case the stack-sortable permutations, which avoid the pattern 231.

Notes
  1. Kitaev (2011), p. 57.
  2. Bose, Buss & Lubiw (1998); Kitaev (2011), Theorem 2.2.36, p. p.58.
  3. Ghys (2016), p. 15.
  4. See Kitaev (2011), Theorem 2.2.45, p. 60.
  5. Bouvel, Rossin & Vialette (2007).
  6. Bose, Buss & Lubiw (1998).
  7. Szepieniec & Otten (1980); Ackerman, Barequet & Pinter (2006)
gollark: Maybe I should Laplace-transform Palaiologos now, for purposes.
gollark: osmarkscalculator™ doesn't know it.
gollark: Really? Oops.
gollark: Sufficiently general pattern matching is rather hard, so it cannot differentiate palaiologes.
gollark: osmarkscalculator™ can't really do those.

References
  • Ackerman, Eyal; Barequet, Gill; Pinter, Ron Y. (2006), "A bijection between permutations and floorplans, and its applications", Discrete Applied Mathematics, 154 (12): 1674–1684, doi:10.1016/j.dam.2006.03.018, MR 2233287
  • Avis, David; Newborn, Monroe (1981), "On pop-stacks in series", Utilitas Mathematica, 19: 129–140, MR 0624050.
  • Bouvel, Mathilde; Rossin, Dominique; Vialette, Stéphane (2007), "Longest common separable pattern among permutations", Combinatorial Pattern Matching (CPM 2007), Lecture Notes in Computer Science, 4580, Springer, pp. 316–327, doi:10.1007/978-3-540-73437-6_32, ISBN 978-3-540-73436-9.
  • Bose, Prosenjit; Buss, Jonathan; Lubiw, Anna (1998), "Pattern matching for permutations", Information Processing Letters, 65 (5): 277–283, CiteSeerX 10.1.1.39.3641, doi:10.1016/S0020-0190(97)00209-3, MR 1620935.
  • Ghys, Étienne (2016), A Singular Mathematical Promenade, arXiv:1612.06373, Bibcode:2016arXiv161206373G.
  • Kitaev, Sergey (2011), "2.2.5 Separable permutations", Patterns in permutations and words, Monographs in Theoretical Computer Science. An EATCS Series, Berlin: Springer-Verlag, pp. 57–66, doi:10.1007/978-3-642-17333-2, ISBN 978-3-642-17332-5, Zbl 1257.68007.
  • Shapiro, Louis; Stephens, Arthur B. (1991), "Bootstrap percolation, the Schröder numbers, and the N-kings problem", SIAM Journal on Discrete Mathematics, 4 (2): 275–280, doi:10.1137/0404025, MR 1093199.
  • Szepieniec, A. A.; Otten, R. H. J. M. (1980), "The genealogical approach to the layout problem", 17th Conf. on Design Automation (DAC 1980), pp. 535–542, doi:10.1109/DAC.1980.1585298 (inactive 2020-01-22).
  • West, Julian (1995), "Generating trees and the Catalan and Schröder numbers", Discrete Mathematics, 146 (1–3): 247–262, doi:10.1016/0012-365X(94)00067-1, MR 1360119.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.