Seconds pendulum

A seconds pendulum is a pendulum whose period is precisely two seconds; one second for a swing in one direction and one second for the return swing, a frequency of 1/2 Hz.[1]

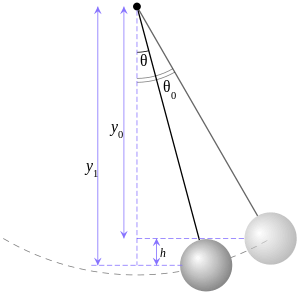
The second pendulum, with a period of two seconds so each swing takes one second
A simple pendulum exhibits approximately simple harmonic motion under the conditions of no damping and small amplitude.

Pendulum

A pendulum is a weight suspended from a pivot so that it can swing freely. When a pendulum is displaced sideways from its resting equilibrium position, it is subject to a restoring force due to gravity that will accelerate it back toward the equilibrium position. When released, the restoring force combined with the pendulum's mass causes it to oscillate about the equilibrium position, swinging back and forth. The time for one complete cycle, a left swing and a right swing, is called the period. The period depends on the length of the pendulum, and also to a slight degree on its weight distribution (the moment of inertia about its own center of mass) and the amplitude (width) of the pendulum's swing.

For a point mass on a weightless string of length L swinging with an infinitesimally small amplitude, without resistance, the length of the string of a seconds pendulum is equal to L = g/π2 where g is the acceleration due to gravity, with units of length per second squared, and L is the length of the string in the same units. Using the SI recommended acceleration due to gravity of g0 = 9.80665 m/s2, the length of the string will be approximately 993.6 millimeters, i.e. less than a centimeter short of one meter everywhere on Earth.

Defining the second
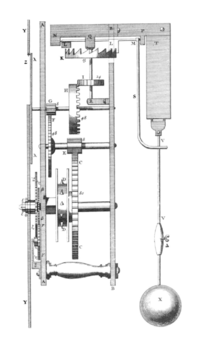
The second pendulum clock built around 1673 by Christiaan Huygens, inventor of the pendulum clock. Drawing is from his treatise Horologium Oscillatorium, published 1673, Paris, and it records improvements to the mechanism that Huygens had illustrated in the 1658 publication of his invention, titled Horologium. It is a weight-driven clock (the weight chain is removed) with a verge escapement (K,L), with the 1 second pendulum (X) suspended on a cord (V). The large metal plate (T) in front of the pendulum cord is the first illustration of Huygens' 'cycloidal cheeks', an attempt to improve accuracy by forcing the pendulum to follow a cycloidal path, making its swing isochronous. Huygens claimed it achieved an accuracy of 10 seconds per day.

The pendulum clock was invented in 1656 by Dutch scientist and inventor Christiaan Huygens, and patented the following year. Huygens contracted the construction of his clock designs to clockmaker Salomon Coster, who actually built the clock. Huygens was inspired by investigations of pendulums by Galileo Galilei beginning around 1602. Galileo discovered the key property that makes pendulums useful timekeepers: isochronism, which means that the period of swing of a pendulum is approximately the same for different sized swings.[2][3] Galileo had the idea for a pendulum clock in 1637, which was partly constructed by his son in 1649, but neither lived to finish it.[4] The introduction of the pendulum, the first harmonic oscillator used in timekeeping, increased the accuracy of clocks enormously, from about 15 minutes per day to 15 seconds per day[5] leading to their rapid spread as existing 'verge and foliot' clocks were retrofitted with pendulums.

These early clocks, due to their verge escapements, had wide pendulum swings of 80–100°. In his 1673 analysis of pendulums, Horologium Oscillatorium, Huygens showed that wide swings made the pendulum inaccurate, causing its period, and thus the rate of the clock, to vary with unavoidable variations in the driving force provided by the movement. Clockmakers' realisation that only pendulums with small swings of a few degrees are isochronous motivated the invention of the anchor escapement around 1670, which reduced the pendulum's swing to 4–6°.[6] The anchor became the standard escapement used in pendulum clocks. In addition to increased accuracy, the anchor's narrow pendulum swing allowed the clock's case to accommodate longer, slower pendulums, which needed less power and caused less wear on the movement. The seconds pendulum (also called the Royal pendulum), 0.994 m (39.1 in) long, in which each swing takes one second, became widely used in quality clocks. The long narrow clocks built around these pendulums, first made by William Clement around 1680, became known as grandfather clocks. The increased accuracy resulting from these developments caused the minute hand, previously rare, to be added to clock faces beginning around 1690.[7]:190

The 18th- and 19th-century wave of horological innovation that followed the invention of the pendulum brought many improvements to pendulum clocks. The deadbeat escapement invented in 1675 by Richard Towneley and popularised by George Graham around 1715 in his precision "regulator" clocks gradually replaced the anchor escapement[7]:181, 441 and is now used in most modern pendulum clocks. The observation that pendulum clocks slowed down in summer brought the realisation that thermal expansion and contraction of the pendulum rod with changes in temperature was a source of error. This was solved by the invention of temperature-compensated pendulums; the mercury pendulum by George Graham in 1721 and the gridiron pendulum by John Harrison in 1726.[7]:193–195 With these improvements, by the mid-18th century precision pendulum clocks achieved accuracies of a few seconds per week.

At the time the second was defined as a fraction of the Earth's rotation time or mean solar day and determined by clocks whose precision was checked by astronomical observations.[8][9] Solar time is a calculation of the passage of time based on the position of the Sun in the sky. The fundamental unit of solar time is the day. Two types of solar time are apparent solar time (sundial time) and mean solar time (clock time).

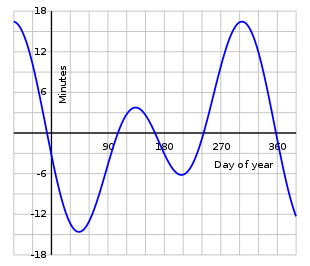
The delay curve—above the axis a sundial will appear fast relative to a clock showing local mean time, and below the axis a sundial will appear slow.

Mean solar time is the hour angle of the mean Sun plus 12 hours. This 12 hour offset comes from the decision to make each day start at midnight for civil purposes whereas the hour angle or the mean sun is measured from the zenith (noon).[10] The duration of daylight varies during the year but the length of a mean solar day is nearly constant, unlike that of an apparent solar day.[11] An apparent solar day can be 20 seconds shorter or 30 seconds longer than a mean solar day.[12] Long or short days occur in succession, so the difference builds up until mean time is ahead of apparent time by about 14 minutes near February 6 and behind apparent time by about 16 minutes near November 3. The equation of time is this difference, which is cyclical and does not accumulate from year to year.

Mean time follows the mean sun. Jean Meeus describes the mean sun as follows:

Consider a first fictitious Sun travelling along the ecliptic with a constant speed and coinciding with the true sun at the perigee and apogee (when the Earth is in perihelion and aphelion, respectively). Then consider a second fictitious Sun travelling along the celestial equator at a constant speed and coinciding with the first fictitious Sun at the equinoxes. This second fictitious sun is the mean Sun..."[13]

In 1936 French and German astronomers found that Earth rotation's speed is irregular. Since 1967 atomic clocks define the second.[14][Note 1]

Usage in metrology

The length of a seconds pendulum was determined (in toises) by Marin Mersenne in 1644. In 1660, the Royal Society proposed that it be the standard unit of length. In 1671 Jean Picard measured this length at the Paris observatory. He found the value of 440.5 lines of the Toise of Châtelet which had been recently renewed. He proposed a universal toise (French: Toise universelle) which was twice the length of the seconds pendulum.[8][15] However, it was soon discovered that the length of a seconds pendulum varies from place to place: French astronomer Jean Richer had measured the 0.3% difference in length between Cayenne (in French Guiana) and Paris.[16]

Relationship to the figure of the Earth
See also: History of the metre § Meridional definition, and Meridian arc § History of measurement

Jean Richer and Giovanni Domenico Cassini measured the parallax of Mars between Paris and Cayenne in French Guiana when Mars was at its closest to Earth in 1672. They arrived at a figure for the solar parallax of 9.5 arcseconds, equivalent to an Earth–Sun distance of about 22000 Earth radii. They were also the first astronomers to have access to an accurate and reliable value for the radius of Earth, which had been measured by their colleague Jean Picard in 1669 as 3269 thousand toises. Picard's geodetic observations had been confined to the determination of the magnitude of the earth considered as a sphere, but the discovery made by Jean Richer turned the attention of mathematicians to its deviation from a spherical form. The determination of the figure of the earth became a problem of the highest importance in astronomy, inasmuch as the diameter of the earth was the unit to which all celestial distances had to be referred.[17][18][19][20][8][21]

British physicist Isaac Newton, who used Picard's Earth measurement for establishing his law of universal gravity,[22] explained this variation of the seconds pendulum's length in his Principia Mathematica (1687) in which he outlined his theory and calculations on the shape of the Earth. Newton theorized correctly that the Earth was not precisely a sphere but had an oblate ellipsoidal shape, slightly flattened at the poles due to the centrifugal force of its rotation. Since the surface of the Earth is closer to its center at the poles than at the equator, gravity is stronger there. Using geometric calculations, he gave a concrete argument as to the hypothetical ellipsoid shape of the Earth.[23]

The goal of Principia was not to provide exact answers for natural phenomena, but to theorize potential solutions to these unresolved factors in science. Newton pushed for scientists to look further into the unexplained variables. Two prominent researchers that he inspired were Alexis Clairaut and Pierre Louis Maupertuis. They both sought to prove the validity of Newton's theory on the shape of the Earth. In order to do so, they went on an expedition to Lapland in an attempt to accurately measure the meridian arc. From such measurements they could calculate the eccentricity of the Earth, its degree of departure from a perfect sphere. Clairaut confirmed that Newton's theory that the Earth was ellipsoidal was correct, but his calculations were in error, and wrote a letter to the Royal Society of London with his findings.[24] The society published an article in Philosophical Transactions the following year in 1737 that revealed his discovery. Clairaut showed how Newton's equations were incorrect, and did not prove an ellipsoid shape to the Earth.[25] However, he corrected problems with the theory, that in effect would prove Newton's theory correct. Clairaut believed that Newton had reasons for choosing the shape that he did, but he did not support it in Principia. Clairaut's article did not provide a valid equation to back up his argument neither. This created much controversy in the scientific community.

It was not until Clairaut wrote Théorie de la figure de la terre in 1743 that a proper answer was provided. In it, he promulgated what is more formally known today as Clairaut's theorem. By applying Clairaut's theorem, Laplace found from 15 gravity values that the flattening of the Earth was 1/330. A modern estimate is 1/298.25642.[26]

In 1790, one year before the metre was ultimately based on a quadrant of the Earth, Talleyrand proposed that the metre be the length of the seconds pendulum at a latitude of 45°.[1] This option, with one-third of this length defining the foot, was also considered by Thomas Jefferson and others for redefining the yard in the United States shortly after gaining independence from the British Crown.[27]

Drawing of pendulum experiment to determine the length of the seconds pendulum at Paris, conducted in 1792 by Jean-Charles de Borda and Jean-Dominique Cassini. From their original paper. They used a pendulum that consisted of a ​1 1⁄2-inch (3.8 cm) platinum ball suspended by a 12-foot (3.97 m) iron wire (F,Q). It was suspended in front of the pendulum (B) of a precision clock (A).

Instead of the seconds pendulum method, the commission of the French Academy of Sciences – whose members included Lagrange, Laplace, Monge and Condorcet – decided that the new measure should be equal to one ten-millionth of the distance from the North Pole to the Equator (the quadrant of the Earth's circumference), measured along the meridian passing through Paris. Apart from the obvious consideration of safe access for French surveyors, the Paris meridian was also a sound choice for scientific reasons: a portion of the quadrant from Dunkirk to Barcelona (about 1000 km, or one-tenth of the total) could be surveyed with start- and end-points at sea level, and that portion was roughly in the middle of the quadrant, where the effects of the Earth's oblateness were expected to be the largest. The Spanish-French geodetic mission combined with an earlier measurement of the Paris meridian arc and the Lapland geodetic mission had confirmed that the Earth was an oblate spheroid.[21] Moreover, observations were made with a pendulum to determine the local acceleration due to local gravity and centrifugal acceleration; and these observations coincided with the geodetic results in proving that the Earth is flattened at the poles. The acceleration of a body near the surface of the Earth, which is measured with the seconds pendulum, is due to the combined effects of local gravity and centrifugal acceleration. The gravity diminishes with the distance from the center of the Earth while the centrifugal force augments with the distance from the axis of the Earth's rotation, it follows that the resulting acceleration towards the ground is 0.5% greater at the poles than at the Equator and that the polar diameter of the Earth is smaller than its equatorial diameter.[21][28][29][30][Note 2]

The Academy of Sciences planned to infer the flattening of the Earth from the length's differences between meridional portions corresponding to one degree of latitude. Pierre Méchain and Jean-Baptiste Delambre combined their measurements with the results of the Spanish-French geodetic mission and found a value of 1/334 for the Earth's flattening,[31] and they then extrapolated from their measurement of the Paris meridian arc between Dunkirk and Barcelona the distance from the North Pole to the Equator which was 5 130 740 toises. As the metre had to be equal to one ten-millionth of this distance, it was defined as 0.513074 toise or 3 feet and 11.296 lines of the Toise of Peru.[32] The Toise of Peru had been constructed in 1735 as the standard of reference in the Spanish-French Geodesic Mission, conducted in actual Ecuador from 1735 to 1744.[33]

Jean-Baptiste Biot and François Arago published in 1821 their observations completing those of Delambre and Mechain. It was an account of the length's variation of the degrees of latitude along the Paris meridian as well as the account of the variation of the seconds pendulum's length along the same meridian between Shetland and the Baleares. The seconds pendulum's length is a mean to measure g, the local acceleration due to local gravity and centrifugal acceleration, which varies depending on one's position on Earth (see Earth's gravity).[34][35][36]

The task of surveying the Paris meridian arc took more than six years (1792–1798). The technical difficulties were not the only problems the surveyors had to face in the convulsed period of the aftermath of the Revolution: Méchain and Delambre, and later Arago, were imprisoned several times during their surveys, and Méchain died in 1804 of yellow fever, which he contracted while trying to improve his original results in northern Spain. In the meantime, the commission of the French Academy of Sciences calculated a provisional value from older surveys of 443.44 lignes. This value was set by legislation on 7 April 1795.[37] While Méchain and Delambre were completing their survey, the commission had ordered a series of platinum bars to be made based on the provisional metre. When the final result was known, the bar whose length was closest to the meridional definition of the metre was selected and placed in the National Archives on 22 June 1799 (4 messidor An VII in the Republican calendar) as a permanent record of the result.[38] This standard metre bar became known as the Committee metre (French : Mètre des Archives).

gollark: We can operate fine at reduced capacity, I suppose.
gollark: You'll need to add the peer config and reload.
gollark: Yes. I'm generating that.
gollark: It's smart enough to not generate loops.
gollark: .

See also

Notes
  1. For further informations see atomic time.
  2. Gravity diminishes proportionally to the square of the distance from the center of the Earth. Centrifugal force is a pseudo force corresponding to inertia and is related to the speed of rotation of an object situated at the surface of the Earth, which is proportional to the distance from the axis of the Earth's rotation: v = 2πR/T.

References
  1. Seconds pendulum
  2. "Huygens' Clocks". Stories. Science Museum, London, UK. Retrieved 14 November 2007.
  3. "Pendulum Clock". The Galileo Project. Rice Univ. Retrieved 3 December 2007.
  4. A modern reconstruction can be seen at "Pendulum clock designed by Galileo, Item #1883-29". Time Measurement. Science Museum, London, UK. Retrieved 14 November 2007.
  5. Bennet, Matthew; et al. (2002). "Huygens' Clocks" (PDF). Georgia Institute of Technology. Archived from the original (PDF) on 10 April 2008. Retrieved 4 December 2007., p. 3, also published in Proceedings of the Royal Society of London, A 458, 563–579
  6. Headrick, Michael (2002). "Origin and Evolution of the Anchor Clock Escapement". Control Systems Magazine. 22 (2). Archived from the original on 26 October 2009. Retrieved 6 June 2007.
  7. Milham, Willis I. (1945), Time and Timekeepers, MacMillan, ISBN 0-7808-0008-7
  8. Picard, Jean (1671). Mesure de la terre (in French). pp. 3–4 – via Gallica.
  9. Alain Bernard (15 April 2018), Le système solaire 2 : La révolution de la Terre, retrieved 12 October 2018
  10. "Solar Apparent Time and Mean Solar Time" (PDF). Archived (PDF) from the original on 28 March 2018. Retrieved 28 March 2018.
  11. For a discussion of the slight changes that affect the mean solar day, see the ΔT article.
  12. "The duration of the true solar day" Archived 2009-08-26 at the Wayback Machine. Pierpaolo Ricci. pierpaoloricci.it. (Italy)
  13. Meeus, J. (1998). Astronomical Algorithms. 2nd ed. Richmond VA: Willmann-Bell. p. 183.
  14. "Revivre notre histoire | Les 350 ans de l'Observatoire de Paris". 350ans.obspm.fr (in French). Retrieved 28 September 2018.
  15. Bigourdan, Guillaume (1901). Le système métrique des poids et mesures ; son établissement et sa propagation graduelle, avec l'histoire des opérations qui ont servi à déterminer le mètre et le kilogramme. University of Ottawa. Paris : Gauthier-Villars. pp. 6–8.
  16. Poynting, John Henry; Thomson, Joseph John (1907). A Textbook of Physics. C. Griffin. pp. 20.
  17. Bond, Peter; Dupont-Bloch, Nicolas (2014). L'exploration du système solaire (in French). Louvain-la-Neuve: De Boeck. pp. 5–6. ISBN 9782804184964. OCLC 894499177.
  18. "Première détermination de la distance de la Terre au Soleil | Les 350 ans de l'Observatoire de Paris". 350ans.obspm.fr (in French). Retrieved 2 October 2018.
  19. "1967LAstr..81..234G Page 234". adsbit.harvard.edu. Retrieved 2 October 2018.
  20. "INRP - CLEA - Archives : Fascicule N° 137, Printemps 2012 Les distances". clea-astro.eu (in French). Retrieved 2 October 2018.
  21. Clarke, Alexander Ross; Helmert, Friedrich Robert (1911). "Earth, Figure of the" . In Chisholm, Hugh (ed.). Encyclopædia Britannica. 08 (11th ed.). Cambridge University Press.
  22. Biot, Jean-Baptiste; Arago, François (1821). Recueil d'observations géodésiques, astronomiques et physiques, exécutées par ordre du Bureau des longitudes de France, en Espagne, en France, en Angleterre et en Écosse, pour déterminer la variation de la pesanteur et des degrés terrestres sur le prolongement du Méridien de Paris, faisant suite au troisième volume de la Base du Système métrique (in French). p. 523. Retrieved 10 October 2018 – via Gallica.
  23. Newton, Isaac. Principia, Book III, Proposition XIX, Problem III.
  24. Greenburg, John (1995). The Problem of the Earth's Shape from Newton to Clairaut. New York: Cambridge University Press. pp. 132. ISBN 978-0-521-38541-1.
  25. Clairaut, Alexis; Colson, John (1737). "An Inquiry concerning the Figure of Such Planets as Revolve about an Axis, Supposing the Density Continually to Vary, from the Centre towards the Surface". Philosophical Transactions. 40 (449): 277–306. doi:10.1098/rstl.1737.0045. JSTOR 103921.
  26. Table 1.1 IERS Numerical Standards (2003))
  27. Cochrane, Rexmond (1966). "Appendix B: The metric system in the United States". Measures for progress: a history of the National Bureau of Standards. U.S. Department of Commerce. p. 532. Archived from the original on 27 April 2011. Retrieved 5 March 2011.
  28. "Rapport de M. Faye sur un Mémoire de M. Peirce concernant la constance de la pesanteur à Paris et les corrections exigées par les anciennes déterminations de Borda et de Biot". Comptes rendus hebdomadaires des séances de l'Académie des sciences (in French). 90: 1463–1466. 1880. Retrieved 10 October 2018 – via Gallica.
  29. Alain Bernard (29 December 2017), Le système solaire 1: la rotation de la Terre, retrieved 12 October 2018
  30. Cassidy, David C.; Holton, Gerald James; Rutherford, Floyd James; Faye, Vincent; Bréard, Sébastien (2014). Comprendre la physique (in French). Lausanne: Presses polytechniques et universitaires romandes. pp. 173, 149. ISBN 9782889150830. OCLC 895784336.
  31. Levallois, Jean-Jacques (May–June 1986). "L'Académie Royale des Sciences et la Figure de la Terre" [The Royal Academy of Sciences and the Shape of the Earth]. La Vie des Sciences (in French). 3: 290. Bibcode:1986CRASG...3..261L. Retrieved 4 September 2018 – via Gallica.
  32. "Histoire du mètre". Direction Générale des Entreprises (DGE) (in French). Retrieved 28 September 2018.
  33. Clarke, Alexander Ross (1 January 1867). "X. Abstract of the results of the comparisons of the standards of length of England, France, Belgium, Prussia, Russia, India, Australia, made at the ordnance Survey Office, Southampton". Philosophical Transactions of the Royal Society of London. 157: 161–180. doi:10.1098/rstl.1867.0010. ISSN 0261-0523. S2CID 109333769.
  34. Larousse, Pierre (1874). Larousse, Pierre, ed. (1874), "Métrique", Grand dictionnaire universel du XIXe siècle, 11. Paris. pp. 163–164.
  35. Paul., Murdin (2009). Full meridian of glory : perilous adventures in the competition to measure the Earth. New York: Copernicus Books/Springer. ISBN 9780387755342. OCLC 314175913.
  36. Biot, Jean-Baptiste; Arago, François (1821). Recueil d'observations géodésiques, astronomiques et physiques, exécutées par ordre du Bureau des longitudes de France, en Espagne, en France, en Angleterre et en Écosse, pour déterminer la variation de la pesanteur et des degrés terrestres sur le prolongement du Méridien de Paris, faisant suite au troisième volume de la Base du Système métrique (in French). p. 529. Retrieved 21 September 2018 – via Gallica.
  37. National Industrial Conference Board (1921). The metric versus the English system of weights and measures ... The Century Co. pp. 10–11. Retrieved 5 April 2011.
  38.  Larousse, Pierre, ed. (1874), "Métrique", Grand dictionnaire universel du XIXe siècle, 11, Paris: Pierre Larousse, pp. 163–164
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.