Improper rotation

In geometry, an improper rotation,[1] also called rotation-reflection,[2] rotoreflection,[1] rotary reflection,[3] is, depending on context, a linear transformation or affine transformation which is the combination of a rotation about an axis and a reflection in a plane perpendicular to that axis.[4]

Example polyhedra with rotoreflection symmetry
Group S4 S6 S8 S10 S12
Subgroups C2 C3, S2 = Ci C4, C2 C5, S2 = Ci C6, S4, C3, C2
Example
beveled digonal antiprism
triangular antiprism
square antiprism
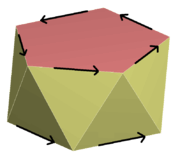pentagonal antiprism
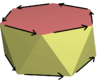hexagonal antiprism
Antiprisms with directed edges have rotoreflection symmetry.
p-antiprisms for odd p contain inversion symmetry, Ci.

Three dimensions
Further information: Point groups in three dimensions
Subgroups for Schoenflies groups S2 to S20

In 3D, equivalently it is the combination of a rotation and an inversion in a point on the axis.[1] Therefore it is also called a rotoinversion or rotary inversion. A three-dimensional symmetry that has only one fixed point is necessarily an improper rotation.[3]

In both cases the operations commute. Rotoreflection and rotoinversion are the same if they differ in angle of rotation by 180°, and the point of inversion is in the plane of reflection.

An improper rotation of an object thus produces a rotation of its mirror image. The axis is called the rotation-reflection axis.[5] This is called an n-fold improper rotation if the angle of rotation is 360°/n.[5] There are several different systems for naming individual improper rotations:

  • The Schoenflies notation uses the symbol Sn (German, Spiegel, for mirror) denotes the symmetry group generated by an n-fold improper rotation. For example, the symmetry operation S6 is the combination of a rotation of (360°/6)=60° and a mirror plane reflection. (This should not to be confused with the same notation for symmetric groups).[5]
  • In Hermann–Mauguin notation the symbol n is used for n-fold rotoinversion; i.e., rotation by an angle of rotation of 360°/n with inversion. Note that 2 is simply a reflection, and is normally denoted m.
  • The Coxeter notation for S2n is [2n+,2+].
  • The Orbifold notation is n×, order 2n.

The direct subgroup of S2n, of index 2, is Cn, [n]+, or (nn), of order n, being the rotoreflection generator applied twice.

S2n for odd n contains an inversion, denoted Ci}}. But for even n S2n does not contain inversion. In general, if odd p is a divisor of n, then S2n/p is a subgroup of S2n. For example S4 is a subgroup of S12.

As an indirect isometry

In a wider sense, an improper rotation may be defined as any indirect isometry; i.e., an element of E(3)\E+(3): thus it can also be a pure reflection in a plane, or have a glide plane. An indirect isometry is an affine transformation with an orthogonal matrix that has a determinant of −1.

A proper rotation is an ordinary rotation. In the wider sense, a proper rotation is defined as a direct isometry; i.e., an element of E+(3): it can also be the identity, a rotation with a translation along the axis, or a pure translation. A direct isometry is an affine transformation with an orthogonal matrix that has a determinant of 1.

In either the narrower or the wider senses, the composition of two improper rotations is a proper rotation, and the composition of an improper and a proper rotation is an improper rotation.

Physical systems

When studying the symmetry of a physical system under an improper rotation (e.g., if a system has a mirror symmetry plane), it is important to distinguish between vectors and pseudovectors (as well as scalars and pseudoscalars, and in general between tensors and pseudotensors), since the latter transform differently under proper and improper rotations (in 3 dimensions, pseudovectors are invariant under inversion).

gollark: Although really, knowing what sets are puts you ahead of the majority of the population.
gollark: This set is actually uncountably infinite.
gollark: Interesting.
gollark: Are you related to the ∀ N∈ ℝ TuxN?
gollark: This has geopolitical implications.

See also

References
  1. Morawiec, Adam (2004), Orientations and Rotations: Computations in Crystallographic Textures, Springer, p. 7, ISBN 9783540407348.
  2. Miessler, Gary; Fischer, Paul; Tarr, Donald (2014), Inorganic Chemistry (5 ed.), Pearson, p. 78
  3. Kinsey, L. Christine; Moore, Teresa E. (2002), Symmetry, Shape, and Surfaces: An Introduction to Mathematics Through Geometry, Springer, p. 267, ISBN 9781930190092.
  4. Salomon, David (1999), Computer Graphics and Geometric Modeling, Springer, p. 84, ISBN 9780387986821.
  5. Bishop, David M. (1993), Group Theory and Chemistry, Courier Dover Publications, p. 13, ISBN 9780486673554.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.