Pitch class space
In music theory, pitch-class space is the circular space representing all the notes (pitch classes) in a musical octave. In this space, there is no distinction between tones that are separated by an integral number of octaves. For example, C4, C5, and C6, though different pitches, are represented by the same point in pitch class space.
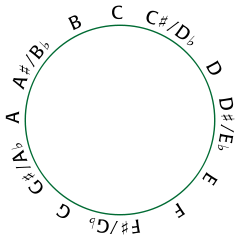
Since pitch-class space is a circle, we return to our starting point by taking a series of steps in the same direction: beginning with C, we can move "upward" in pitch-class space, through the pitch classes C♯, D, D♯, E, F, F♯, G, G♯, A, A♯, and B, returning finally to C. By contrast, pitch space is a linear space: the more steps we take in a single direction, the further we get from our starting point.
Tonal pitch-class space
Deutsch and Feroe (1981), and Lerdahl and Jackendoff (1983) use a "reductional format" to represent the perception of pitch-class relations in tonal contexts. These two-dimensional models resemble bar graphs, using height to represent a pitch class's degree of importance or centricity. Lerdahl's version uses five levels: the first (highest) contains only the tonic, the second contains tonic and dominant, the third contains tonic, mediant, and dominant, the fourth contains all the notes of the diatonic scale, and the fifth contains the chromatic scale. In addition to representing centricity or importance, the individual levels are also supposed to represent "alphabets" that describe the melodic possibilities in tonal music (Lerdahl 2001, 44–46). The model asserts that tonal melodies will be cognized in terms of one of the five levels a-e:
| Level a: | C | C | |||||||||||
| Level b: | C | G | C | ||||||||||
| Level c: | C | E | G | C | |||||||||
| Level d: | C | D | E | F | G | A | B | C | |||||
| Level e: | C | D♭ | D | E♭ | E | F | F♯ | G | A♭ | A | B♭ | B | C |
- (Lerdahl 1992, 113)
Note that Lerdahl's model is meant to be cyclical, with its right edge identical to its left. One could therefore display Lerdahl's graph as a series of five concentric circles representing the five melodic "alphabets." In this way one could unite the circular representation depicted at the beginning of this article with Lerdahl's flat two-dimensional representation depicted above.
According to David Kopp (2002, 1), "Harmonic space, or tonal space as defined by Fred Lerdahl, is the abstract nexus of possible normative harmonic connections in a system, as opposed to the actual series of temporal connections in a realized work, linear or otherwise."
See also
- Pitch circularity
- Pitch interval
- Scientific pitch notation
- Pitch constellation
Sources
- Deutsch, Diana & John Feroe (1981). "The Internal Representation of Pitch Sequences in Tonal Music". Psychological Review. 88 (6): 503–22. doi:10.1037/0033-295X.88.6.503. Full Text
- Kopp, David (2002). Chromatic Transformations in Nineteenth-Century Music. Cambridge University Press. ISBN 978-0-521-80463-9.CS1 maint: ref=harv (link)
- Lerdahl, Fred; Jackendoff, Ray (1983). A Generative Theory of Tonal Music. MIT Press.
- Lerdahl, Fred (1992). "Cognitive Constraints on Compositional Systems". Contemporary Music Review. 6 (2): 97–121. CiteSeerX 10.1.1.168.1343. doi:10.1080/07494469200640161.
- Lerdahl, Fred (2001). Tonal Pitch Space. Oxford and New York: Oxford University Press.CS1 maint: ref=harv (link)
Further reading
- Straus, Joseph (2005). Introduction to Post Tonal Theory (3rd ed.). Up Saddle River, New Jersey: Prentice Hall. ISBN 978-0-13-189890-5.CS1 maint: ref=harv (link)