Parabolic arch

A parabolic arch is an arch in the shape of a parabola.[1] In structures, their curve represents an efficient method of load, and so can be found in bridges and in architecture in a variety of forms.

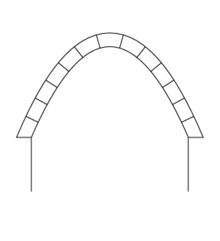
Description

The mathematics

While a parabolic arch may resemble a catenary arch, a parabola is a quadratic function while a catenary is the hyperbolic cosine, cosh(x), a sum of two exponential functions. One parabola is f(x) = x2 + 3x − 1, and hyperbolic cosine is cosh(x) = ex + e−x/2. The curves are unrelated.

The line of thrust

Unlike a catenary arch, the parabolic arch employs the principle that when weight is uniformly applied above, the internal compression (see line of thrust) resulting from that weight will follow a parabolic curve. Of all arch types, the parabolic arch produces the most thrust at the base. Also, it can span the widest area. It is commonly used in bridge design, where long spans are needed.[2][3]

Compared to catenary arches

When an arch carries a uniformly distributed vertical load, the correct shape is a parabola. When an arch carries only its own weight, the best shape is a catenary.[3]

  • A catenary, in blue, graphed against a parabola, in red
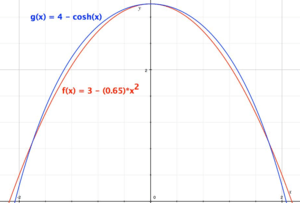  • Parabola (red) graphed against a catenary (blue), view to simulate an arch.
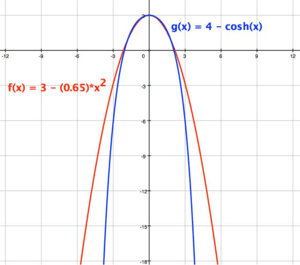  • Parabola (red) graphed against a catenary (blue), view to simulate an arch. Zoomed out.

Uses
Celler modernista,Sant Cugat,

In nature

A hen's egg can be fairly well described as two different paraboloids connected by part of an ellipse .[4][5]

Architectural examples
Former main post office, Utrecht

Self-supporting catenary arches appeared occasionally in ancient architecture, for examples in the main arch of the Taq Kasra in Iran, the largest single-span vault of unreinforced brickwork in the world, and the beehive huts of southwestern Ireland. In the modern period, parabolic arches were first used extensively from the 1880s by the Catalan architect Antoni Gaudí,[6] deriving them from catenary arched shapes, constructed of brick or stone, and culminating in the catenary based design of the famous Sagrada Familia. Other Catalan architects then used them into the 1920s, and they appeared occasionally in German expressionist architecture of the 1920s-30s. From the 1940s they gained a new popularity in reinforced concrete, including in shell concrete forms often as hyperbolic parabloids, especially by Felix Candela in Mexico and Oscar Niemeyer in Brazil, but they could be found around the world, especially for churches, in the 1950s and 60s. Since the 1990s Spanish designer Santiago Calatrava has frequently used parabolas for his signature roof structures and bridges. Structures that are self-supporting arches like the Sheffield Winter Garden are often closer to true catenaries.

Bridges
Garabit viaduct, France

Bridges have used a variety of arches since ancient times, sometimes in very flat segmental arched forms but rarely in the form of a parabola. A simple hanging rope bridge describes a category, but if they were in the form of a suspension bridges they usually describe a parabola in shape, with the roadway hanging from the inverted arch. Modern suspension bridges were built from the early 19th century, beginning with chains and progressing to more and more elegant steel rope examples, and are still in use today. Parabolic arches that support support the roadway from below (or in the form of a through arch) first appeared in the 1870s, and have been used occasionally ever since; examples include :

gollark: Multiplexing CSS transistors can cause lots of collateral damage by affecting many people's connections, so it's not really done often.
gollark: Hey, if you're trying to reconnect the auxiliary CPU alarm, you'll need to do better than posting a vaguely code-looking thing which doesn't work.
gollark: But it definitely would't *work* in anything.
gollark: I mean, maybe esolangs which work by character and ignore invalid ones, sort of thing.
gollark: Seriously. I don't think that's valid syntax in *any programming language at all*.

See also

References
  1. Article about parabolic arch by The Free Dictionary: Parabolic arch | Article about parabolic arch by The Free Dictionary, accessdate: March 2, 2017
  2. Deeks, Andrew J.; Hao, Hong (2004-11-15). Developments in Mechanics of Structures & Materials. ISBN 9789058096593.
  3. The Design of Prestressed Concrete Bridges/Chapter 17 The Design And Construction Of Arches
  4. Rehkugler, G. E. (1973). "Characterizing the Shape of a Hen's Egg" (PDF). Poultry Science. 52: 127–138. doi:10.3382/ps.0520127. Retrieved 22 March 2017.
  5. Google Books: https://books.google.co.uk/books?id=CIAAAAAAMAAJ&pg=PA264&lpg=PA264&dq="hen's+egg"+"parabolic+arch"&source=bl&ots=uOzbRBeDwm&sig=ohyUSTlHvU8sNUqTahR_BjU6gp4&hl=en&sa=X&redir_esc=y#v=onepage&q="hen's egg" "parabolic arch"&f=false, accessdate: March 22, 2017
  6. Chiuini, Michele (2015-05-13). "The parabola of the parabolic arch". IABSE Symposium Report. 104: 1–7. doi:10.2749/222137815815775439.
  7. Interior of St Leonard's church, St... (C) Julian P Guffogg :: Geograph Britain and Ireland: Interior of St Leonard's church, St... (C) Julian P Guffogg :: Geograph Britain and Ireland, accessdate: March 2, 2017
  8. Organ, St Leonard's Parish Church (C) Julian P Guffogg :: Geograph Ireland: para, accessdate: March 3, 2017
  9. "Art, culture and society from Far East". Modello Fantastico. Retrieved 8 Dec 2016.
  10. Jean McConochie photos at pbase.com: para, accessdate: March 3, 2017
  11. "Olafur Eliasson's first building is a castle-like office in a Danish fjord". Dezeen. 2018-06-04. Retrieved 2020-08-12.
  12. "Ponte Maria Pia Bridge". Invention and Technologu.
  13. Weber, Jutta (May 2009). "The Engineer's Aesthetics – Interrelations between Structural Engineering, Architecture and Art" (PDF). Proceedings of the Third International Congress on Construction Histor.
  14. Alamy: para, accessdate: March 4, 2017
  15. Gimeno and Gutierrez. pag.122
  16. Bisbort, Alan (April 10, 1992). "The Draw of Bridges". The Washington Post. pp. A8–A9.
  17. The Victoria Falls Bridge: To the Victoria Falls - The Victoria Falls Bridge, accessdate: March 2, 2017
  18. Livingstone News: central, accessdate: March 2, 2017
  19. Best Bridge Africa Victoria Falls Bridge: Best Bridge Africa Victoria Falls Bridge, accessdate: March 2, 2017
  20. Arch Bridges on Waymarking.com: Memorial Bridge - Springfield/West Springfield, MA - Arch Bridges on Waymarking.com, accessdate: March 4, 2017
  21. "Tyne Bridge". BBC Inside Out. 24 September 2014. Retrieved 3 March 2017.
  22. Style & Vernacular: A Guide to the Architecture of Lane County, Oregon. Western Imprints, The Press of the Oregon Historical Society. 1983. p. 151. ISBN 978-0-87595-085-3.
  23. The New York Times: parab, accessdate: March 3, 2017
  24. Bixby Creek Bridge on Highway One from the Pat Hathaway Photo Collection: Bixby Creek Bridge on Highway One from the Pat Hathaway Photo Collection, accessdate: March 6, 2017
  25. Heritage New Zealand: www.heritage.org.nz/the-list/details/5180, accessdate: March 3, 2017

Bibliography
  • Gimeno Díaz de Atauri, Jorge; Gutiérrez Andrés, Juan (2001), El Puente de la Pólvora y otros puentes, Murcia: Colegio de Ingenieros de Caminos, Canales y Puentes. Demarcación Murcia, ISBN 978-84-607-3209-9
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.