Hyperrectangle

In geometry, an n-orthotope[2] (also called a hyperrectangle or a box) is the generalization of a rectangle for higher dimensions, formally defined as the Cartesian product of intervals.

Hyperrectangle
n-orthotope

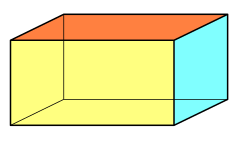A rectangular cuboid is a 3-orthotope
TypePrism
Facets2n
Vertices2n
Schläfli symbol{} × {} ... × {}[1]
Coxeter-Dynkin diagram ...
Symmetry group[2n−1], order 2n
DualRectangular n-fusil
Propertiesconvex, zonohedron, isogonal

Types

A three-dimensional orthotope is also called a right rectangular prism, rectangular cuboid, or rectangular parallelepiped.

A special case of an n-orthotope, where all edges are equal length, is the n-cube.[2]

By analogy, the term "hyperrectangle" or "box" refers to Cartesian products of orthogonal intervals of other kinds, such as ranges of keys in database theory or ranges of integers, rather than real numbers.[3]

Dual polytope
n-fusil

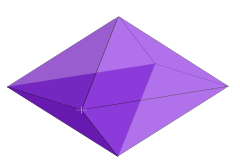Example: 3-fusil
Facets2n
Vertices2n
Schläfli symbol{} + {} + ... + {}
Coxeter-Dynkin diagram ...
Symmetry group[2n−1], order 2n
Dualn-orthotope
Propertiesconvex, isotopal

The dual polytope of an n-orthotope has been variously called a rectangular n-orthoplex, rhombic n-fusil, or n-lozenge. It is constructed by 2n points located in the center of the orthotope rectangular faces.

An n-fusil's Schläfli symbol can be represented by a sum of n orthogonal line segments: { } + { } + ... + { }.

A 1-fusil is a line segment. A 2-fusil is a rhombus. Its plane cross selections in all pairs of axes are rhombi.

n Example image
1
{ }
2
{ } + { }
3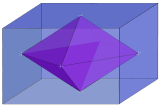
Rhombic 3-orthoplex inside 3-orthotope
{ } + { } + { }
gollark: ++help
gollark: Sounds helpful, thanks.
gollark: Yes, I know how to detect a timeout, just not how to stop the thread.
gollark: If I understand correctly, that requires cooperation from the other thread.
gollark: Yes, exactly.

See also

Notes
  1. N.W. Johnson: Geometries and Transformations, (2018) ISBN 978-1-107-10340-5 Chapter 11: Finite symmetry groups, 11.5 Spherical Coxeter groups, p.251
  2. Coxeter, 1973
  3. See e.g. Zhang, Yi; Munagala, Kamesh; Yang, Jun (2011), "Storing matrices on disk: Theory and practice revisited" (PDF), Proc. VLDB, 4 (11): 1075–1086.

References
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.