Magic graph

A magic graph is a graph whose edges are labelled by positive integers, so that the sum over the edges incident with any vertex is the same, independent of the choice of vertex; or it is a graph that has such a labelling. If the integers are the first q positive integers, where q is the number of edges, the graph and the labelling are called supermagic.

A graph is vertex-magic if its vertices can be labelled so that the sum on any edge is the same. It is total magic if its edges and vertices can be labelled so that the vertex label plus the sum of labels on edges incident with that vertex is a constant.

There are a great many variations on the concept of magic labelling of a graph. There is much variation in terminology as well. The definitions here are perhaps the most common.

Comprehensive references for magic labellings and magic graphs are Gallian (1998), Wallis (2001), and Marr and Wallis (2013).

Magic squares
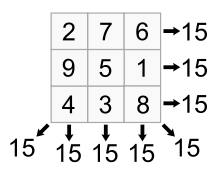
Euler diagram of requirements of some types of 4×4 magic squares. Cells of the same colour sum to the magic constant. * In 4×4 most-perfect magic squares, any 2 cells that are 2 cells diagonally apart (including wraparound) sum to half the magic constant, hence any 2 such pairs also sum to the magic constant.

A semimagic square is an n × n square with the numbers 1 to n2 in its cells, in which the sum of each row and column is the same. A semimagic square is equivalent to a magic labelling of the complete bipartite graph Kn,n. The two vertex sets of Kn,n correspond to the rows and the columns of the square, respectively, and the label on an edge risj is the value in row i, column j of the semimagic square.

The definition of semimagic squares differs from the definition of magic squares in the treatment of the diagonals of the square. Magic squares are required to have diagonals with the same sum as the row and column sums, but for semimagic squares this is not required. Thus, every magic square is semimagic, but not vice versa.

gollark: I mean, ironical™, but he seems mostly ifne.
gollark: HelloBoi's powers are unlimited.
gollark: I mean, you can losslessly compress PNGs a few percent, but I doubt they'd put in the CPU time.
gollark: I don't think so.
gollark: No, they're PNGs.

References
  • W. D. Wallis (2001), Magic Graphs. Birkhäuser Boston, Boston, Mass. ISBN 0-8176-4252-8
  • Alison M. Marr and W. D. Wallis (2013), Magic Graphs. Second edition. Birkhäuser/Springer, New York. ISBN 978-0-8176-8390-0; 978-0-8176-8391-7
  • Joseph A. Gallian (1998), A dynamic survey of graph labeling. Electronic Journal of Combinatorics, vol. 5, Dynamic Survey 6. Updated several times.


This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.