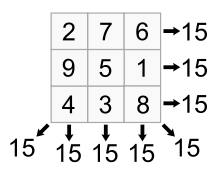
Antimagic square

An antimagic square of order n is an arrangement of the numbers 1 to n² in a square, such that the sums of the n rows, the n columns and the two diagonals form a sequence of 2n + 2 consecutive integers. The smallest antimagic squares have order 4.[1] Antimagic squares contrast with magic squares, where each row, column, and diagonal sum must have the same value.[2]

Examples

Order 4 antimagic squares

2 15 5 13 16 3 7 12 9 8 14 1 6 4 11 10

1 13 3 12 15 9 4 10 7 2 16 8 14 6 11 5

In both of these antimagic squares of order 4, the rows, columns and diagonals sum to ten different numbers in the range 29–38.[2]

Order 5 antimagic squares

5 8 20 9 22 19 23 13 10 2 21 6 3 15 25 11 18 7 24 1 12 14 17 4 16

21 18 6 17 4 7 3 13 16 24 5 20 23 11 1 15 8 19 2 25 14 12 9 22 10

In the antimagic square of order 5 on the left, the rows, columns and diagonals sum up to numbers between 60 and 71.[2] In the antimagic square on the right, the rows, columns and diagonals add up to numbers between 59-70.[1]

Open problems

The following questions about antimagic squares have not been solved.

• How many antimagic squares of a given order exist?
• Do antimagic squares exist for all orders greater than 3?
• Is there a simple proof that no antimagic square of order 3 exists?

Generalizations

A sparse antimagic square (SAM) is a square matrix of size n by n of nonnegative integers whose nonzero entries are the consecutive integers ${\displaystyle 1,\ldots ,m}$ for some ${\displaystyle m\leq n^{2}}$, and whose row-sums and column-sums constitute a set of consecutive integers.[3] If the diagonals are included in the set of consecutive integers, the array is known as a sparse totally anti-magic square (STAM). Note that a STAM is not necessarily a SAM, and vice versa.

A filling of the n × n square with the numbers 1 to n² in a square, such that the rows, columns, and diagonals all sum to different values has been called a heterosquare.[4] (Thus, they are the relaxation in which no particular values are required for the row, column, and diagonal sums.) There are no heterosquares of order 2, but heterosquares exist for any order n ≥ 3: if n is odd, filling the square in a spiral pattern will produce a heterosquare.[4] And if n is even, a heterosquare results from writing the numbers 1 to n² in order, then exchanging 1 and 2. It is suspected that there are exactly 3120 essentially different heterosquares of order 3.[5]

See also

• Magic square
• J. A. Lindon

References

1. W., Weisstein, Eric. "Antimagic Square". mathworld.wolfram.com. Retrieved 2016-12-03.
2. "Anti-magic Squares". www.magic-squares.net. Retrieved 2016-12-03.
3. Gray, I. D.; MacDougall, J.A. (2006). "Sparse anti-magic squares and vertex-magic labelings of bipartite graphs". Discrete Mathematics. 306 (22): 2878–2892. doi:10.1016/j.disc.2006.04.032.
4. Weisstein, Eric W. "Heterosquare". MathWorld.
5. Peter Bartsch's Heterosquares at magic-squares.net

External links

• Weisstein, Eric W. "Antimagic Square". MathWorld.