Macrocyclic stereocontrol

Macrocyclic stereocontrol refers to the directed outcome of a given intermolecular or intramolecular chemical reaction, generally an organic reaction, that is governed by the conformational or geometrical preference of a carbocyclic or heterocyclic ring, where the ring containing 8 or more atoms.

Introduction

Stereocontrol for cyclohexane rings is well established in organic chemistry, in large part due to the axial/equatorial preferential positioning of substituents on the ring. Macrocyclic stereocontrol models the substitution and reactions of medium and large rings in organic chemistry, with remote stereogenic elements providing enough conformational influence to direct the outcome of a reaction.

Early assumptions towards macrocycles in synthetic chemistry considered them far too floppy to provide any degree of stereochemical or regiochemical control in a reaction. The experiments of W. Clark Still in the late 1970s and 1980s challenged this assumption,[1] while several others found crystallographic data [2] and NMR data [3] that suggested macrocyclic rings were not the floppy, conformationally ill-defined species many assumed.

The degree to which a macrocyclic ring is either rigid or floppy depends significantly on the substitution of the ring and the overall size.[4][5] Significantly, even small conformational preferences, such as those envisioned in floppy macrocycles, can profoundly influence the ground state of a given reaction, providing stereocontrol such as in the synthesis of miyakolide.[6] Computational modeling can predict conformations of medium rings with reasonable accuracy, as Still used molecular mechanics modeling computations to predict ring conformations to determine potential reactivity and stereochemical outcomes.[1]

Reaction classes used in synthesis of natural products under the macrocyclic stereocontrol model for obtaining a desired stereochemistry include: hydrogenations such as in neopeltolide [7] and (±)-methynolide,[8] epoxidations such as in (±)-periplanone B[9] and lonomycin A,[10] hydroborations such as in 9-dihydroerythronolide B,[11] enolate alkylations such as in (±)-3-deoxyrosaranolide,[12] dihydroxylations such as in cladiell-11-ene-3,6,7-triol,[13] and reductions such as in eucannabinolide.[14]

Conformational preferences

Macrocycles can access a number of stable conformations, with preferences to reside in those that minimize the number of transannular nonbonded interactions within the ring.[5] Medium rings (8-11 atoms) are the most strained with between 9-13 (kcal/mol) strain energy; analysis of the factors important in considering larger macrocyclic conformations can thus be modeled by looking at medium ring conformations.[15] Conformational analysis of odd-membered rings suggests they tend to reside in less symmetrical forms with smaller energy differences between stable conformations.[16]

Cyclooctane

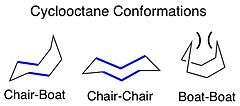
Conformational analysis of medium rings begins with examination of cyclooctane. Spectroscopic methods have determined that cyclooctane possesses three main conformations: chair-boat, chair-chair, and boat-boat. Cyclooctane prefers to reside in a chair-boat conformation, minimizing the number of eclipsing ethane interactions (shown in blue), as well as torsional strain.[17] The chair-chair conformation is the second most abundant conformation at room temperature, with a ratio of 96:4 chair-boat:chair-chair observed.[1]

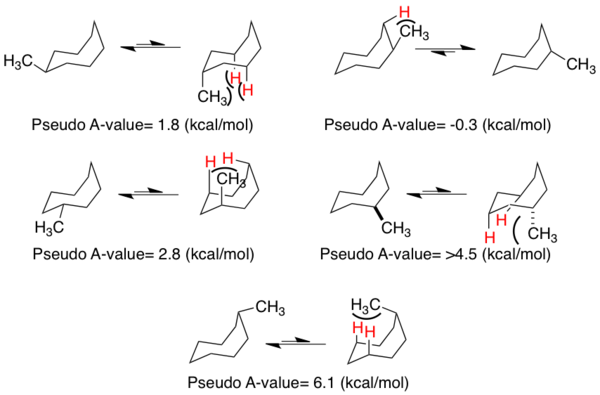
Substitution positional preferences in the ground state conformer of methyl cyclooctane can be approximated using parameters similar to those for smaller rings. In general, the substituents exhibit preferences for equatorial placement, except for the lowest energy structure (pseudo A-value of -0.3 kcal/mol in figure below) in which axial substitution is favored. The "pseudo A-value" is best treated as the approximate energy difference between placing the methyl substituent in the equatorial or axial positions. The most energetically unfavorable interaction involves axial substitution at the vertex of the boat portion of the ring (6.1 kcal/mol).

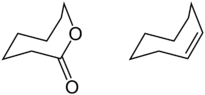
These energetic differences can help rationalize the lowest energy conformations of 8 atom ring structures containing an sp2 center. In these structures, the chair-boat is the ground state model, with substitution forcing the structure to adopt a conformation such that non-bonded interactions are minimized from the parent structure.[18] From the cyclooctene figure below, it can be observed that one face is more exposed than the other, foreshadowing a discussion of privileged attack angles (see peripheral attack).

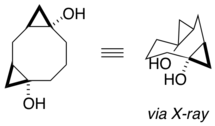
X-ray analysis of functionalized cyclooctanes provided proof of conformational preferences in these medium rings. Significantly, calculated models matched the obtained X-ray data, indicating that computational modeling of these systems could in some cases quite accurately predict conformations. The increased sp2 character of the cyclopropane rings favor them to be placed similarly such that they relieve non-bonded interactions.[19]

Cyclodecane

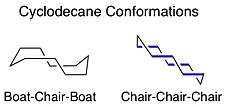
Similar to cyclooctane, a cyclodecane ring exhibits several conformations with two lower energy conformations. The boat-chair-boat conformation is energetically minimized, while the chair-chair-chair conformation has significant eclipsing interactions.

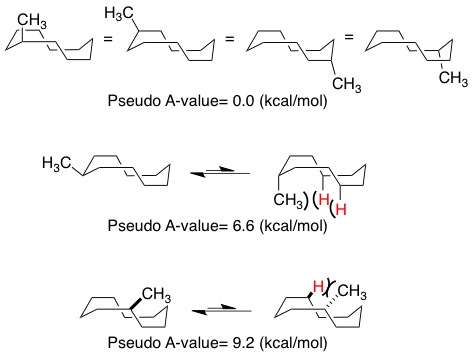
These ground-state conformational preferences are useful analogies to more highly functionalized macrocyclic ring systems, where local effects can still be governed to first approximation by energy minimized conformations even though the larger ring size allows more conformational flexibility of the entire structure. For example, in methyl cyclodecane, the ring can be expected to adopt the minimized conformation of boat-chair-boat. The figure below shows the energetic penalty between placing the methyl group at certain sites within the boat-chair-boat structure. Unlike canonical small ring systems, the cyclodecane system with the methyl group placed at the "corners" of the structure exhibits no preference for axial vs. equatorial positioning due to the presence of an unavoidable gauche-butane interaction in both conformations. Significantly more intense interactions develop when the methyl group is placed in the axial position at other sites in the boat-chair-boat conformation.[1]

Larger ring systems

Similar principles guide the lowest energy conformations of larger ring systems. Along with the acyclic stereocontrol principles outlined below, subtle interactions between remote substituents in large rings, analogous to those observed for 8-10 membered rings, can influence the conformational preferences of a molecule. In conjunction with remote substituent effects, local acyclic interactions can also play an important role in determining the outcome of macrocyclic reactions.[20] The conformational flexibility of larger rings potentially allows for a combination of acyclic and macrocyclic stereocontrol to direct reactions.[20]

Reactivity and conformational preferences

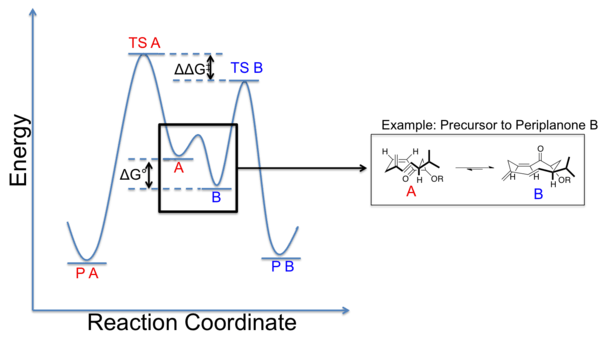
The stereochemical result of a given reaction on a macrocycle capable of adopting several conformations can be modeled by a Curtin-Hammett scenario. In the diagram below, the two ground state conformations exist in an equilibrium, with some difference in their ground state energies. Conformation B is lower in energy than conformation A, and while possessing a similar energy barrier to its transition state in a hypothetical reaction, thus the product formed is predominantly product B (P B) arising from conformation B via transition state B (TS B). The inherent preference of a ring to exist in one conformation over another provides a tool for stereoselective control of reactions by biasing the ring into a given configuration in the ground state. The energy differences, ΔΔG‡ and ΔG0 are significant considerations in this scenario. The preference for one conformation over another can be characterized by ΔG0, the free energy difference, which can, at some level, be estimated from conformational analysis. The free energy difference between the two transition states of each conformation on its path to product formation is given by ΔΔG‡. The value of ΔG0 between not just one, but many accessible conformations is the underlying energetic impetus for reactions occurring from the most stable ground state conformation and is the crux of the peripheral attack model outlined below.[21]

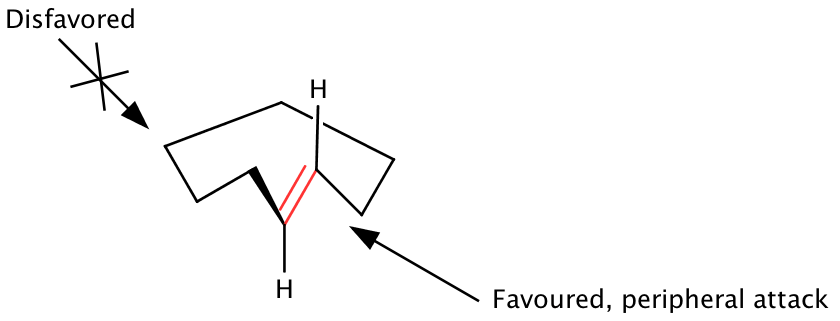
The peripheral attack model

Macrocyclic rings containing sp2 centers display a conformational preference for the sp2 centers to avoid transannular nonbonded interactions by orienting perpendicular to the plan of the ring. Clark W. Still proposed that the ground state conformations of macrocyclic rings, containing the energy minimized orientation of the sp2 center, display one face of an olefin outwards from the ring.[1][9][12] Addition of reagents from the outside the olefin face and the ring (peripheral attack) is thus favored, while attack from across the ring on the inward diastereoface is disfavored. Ground state conformations dictate the exposed face of the reactive site of the macrocycle, thus both local and distant stereocontrol elements must be considered. The peripheral attack model holds well for several classes of macrocycles, though relies on the assumption that ground state geometries remain unperturbed in the corresponding transition state of the reaction.

Intermolecular reactions

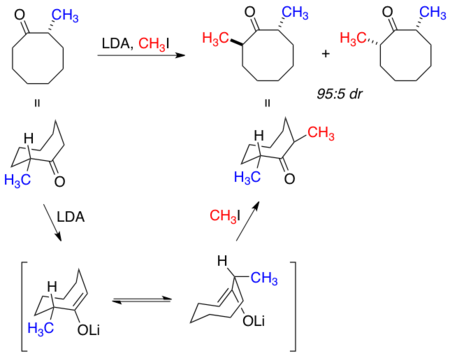
Early investigations of macrocyclic stereocontrol studied the alkylation of 8-membered cyclic ketones with varying substitution.[1] In the example below, alkylation of 2-methylcyclooctanone occurred to yield the predominantly trans product. Proceeding from the lowest energy conformation of 2-methylcycloctanone, peripheral attack is observed from either one of the low energy (energetic difference of 0.5 (kcal/mol)) enolate conformations, resulting in a trans product from either of the two depicted transition state conformations.[22]

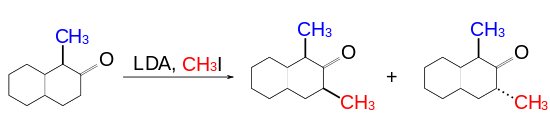
Unlike the cyclooctanone case, alkylation of 2-cyclodecanone rings does not display significant diastereoselectivity.[1]

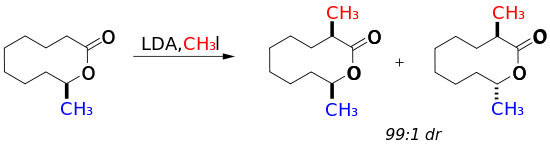
However, 10-membered cyclic lactones display significant diastereoselectivity.[1] The proximity of the methyl group to the ester linkage was directly correlated with the diastereomeric ratio of the reaction products, with placement at the 9 position (below) yielding the highest selectivity. In contrast, when the methyl group was placed at the 7 position, a 1:1 mixture of diastereomers was obtained. Placement of the methyl group at the 9-position in the axial position yields the most stable ground state conformation of the 10-membered ring leading to high diastereoselectivity.

Conjugate addition to the E-enone below also follows the expected peripheral attack model to yield predominantly trans product.[22] High selectivity in this addition can be attributed to the placement of sp2 centers such that transannular nonbonded interactions are minimized, while also placing the methyl substitution in the more energetically favorable position for cyclodecane rings. This ground state conformation heavily biases conjugate addition to the less hindered diastereoface.

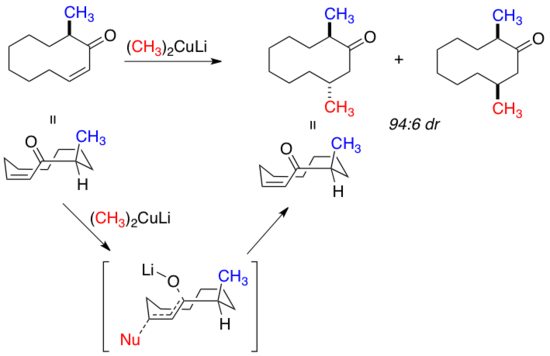
Intramolecular reactions

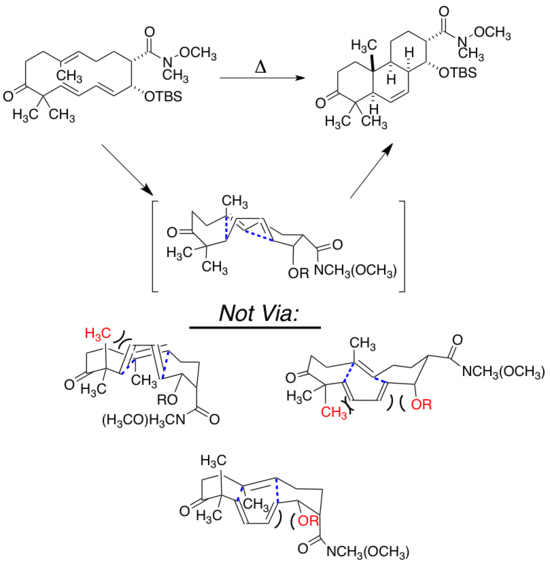
Similar to intermolecular reactions, intramolecular reactions can show significant stereoselectivity from the ground state conformation of the molecule. In the intramolecular Diels-Alder reaction depicted below, the lowest energy conformation yields the observed product.[23] The structure minimizing repulsive steric interactions provides the observed product by having the lowest barrier to a transition state for the reaction. Though no external attack by a reagent occurs, this reaction can be though of similarly to those modeled with peripheral attack; the lowest energy conformation is the most likely to react for a given reaction.

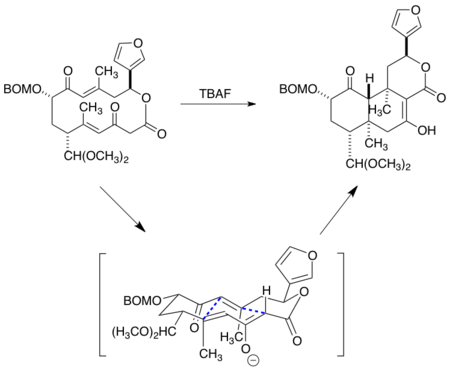
The lowest energy conformations of macrocycles also influence intramolecular reactions involving transannular bond formation. In the intramolecular Michael addition sequence below, the ground state conformation minimizes transannular interactions by placing the sp2 centers at the appropriate vertices, while also minimizing diaxial interactions.[24]

Prominent examples in synthesis

These principles have been applied in multiple natural product targets containing medium and large rings. The syntheses of cladiell-11-ene-3,6,7- triol,[13] (±)-periplanone B,[9] eucannabinolide,[14] and neopeltolide[7] are all significant in their usage of macrocyclic stereocontrol en route to obtaining the desired structural targets.

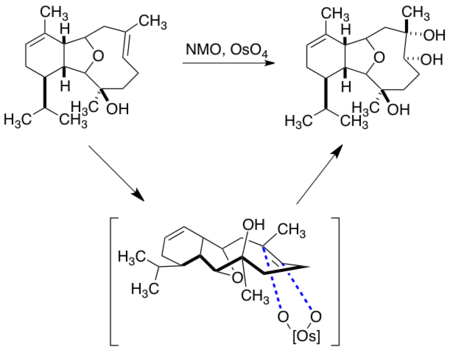
Cladiell-11-ene-3,6,7-triol

The cladiellin family of marine natural products possess interesting molecular architecture, generally containing a 9-membered medium-sized ring. The synthesis of (−)-cladiella-6,11-dien-3-ol allowed access to a variety of other members of the cladiellin family. Notably, the conversion to cladiell-11-ene-3,6,7-triol makes use of macrocyclic stereocontrol in the dihydroxylation of a trisubstituted olefin. Below is shown the synthetic step controlled by the ground state conformation of the macrocycle, allowing stereoselective dihydroxylation without the usage of an asymmetric reagent. This example of substrate controlled addition is an example of the peripheral attack model in which two centers on the molecule are added two at once in a concerted fashion.

(±)-Periplanone B

The synthesis of (±)-periplanone B is a prominent example of macrocyclic stereocontrol.[9] Periplanone B is a sex pheromone of the American female cockroach, and has been the target of several synthetic attempts. Significantly, two reactions on the macrocyclic precursor to (±)-periplanone B were directed using only ground state conformational preferences and the peripheral attack model. Reacting from the most stable boat-chair-boat conformation, asymmetric epoxidation of the cis-internal olefin can be achieved without using a reagent-controlled epoxidation method or a directed epoxidation with an allylic alcohol.

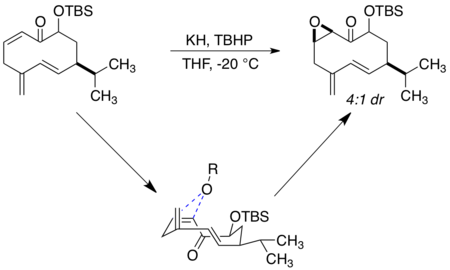
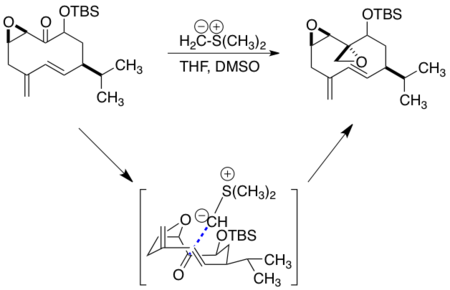
Epoxidation of the ketone was achieved, and can be modeled by peripheral attack of the sulfur ylide on the carbonyl group in a Johnson-Corey-Chaykovsky reaction to yield the protected form of (±)-periplanone B. Deprotection of the alcohol followed by oxidation yielded the desired natural product.

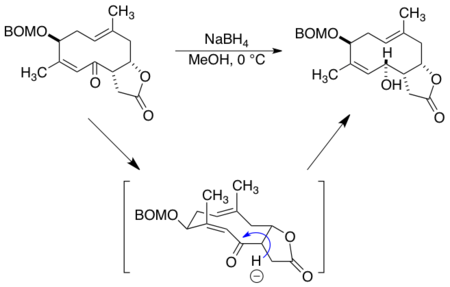
Eucannabinolide

In the synthesis of the cytotoxic germacranolide sesquiterpene eucannabinolide, Still demonstrates the application of the peripheral attack model to the reduction of a ketone to set a new stereocenter using NaBH4. Significantly, the synthesis of eucannabinolide relied on the usage of molecular mechanics (MM2) computational modeling to predict the lowest energy conformation of the macrocycle to design substrate-controlled stereochemical reactions.

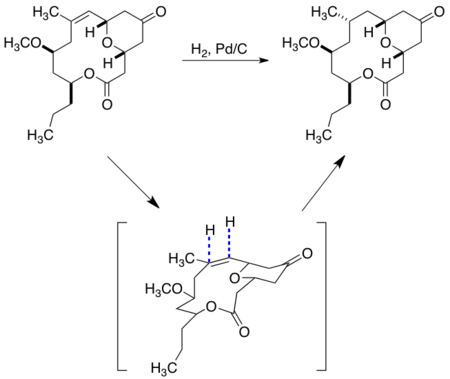
Neopeltolide

Neopeltolide was originally isolated from sponges near the Jamaican coast and exhibits nanomolar cytoxic activity against several lines of cancer cells. The synthesis of the neopeltolide macrocyclic core displays a hydrogenation controlled by the ground state conformation of the macrocycle.

Criticisms

The peripheral attack model is based on predicting lowest energy conformations of an inherently complicated system, where nuanced perturbations can cause huge stereodifferentiating consequences. By modeling peripheral attack using the Curtin-Hammett scenario depicted above, the transition state is excluded from this conformation analysis by assuming that the barrier to each transition state from a given conformation is the same and thus that ground state conformations are the sole product determining factor. A significant criticism is the mapping of medium-sized ring conformations and influences onto larger ring systems. Macrocycles can possess varying degrees of rigidity in their structure, making a single peripheral attack model difficult to apply to all systems. Different classes of reactions might not fit the peripheral attack model, as reactions such as epoxidations, hydroxylations, alkylations, and reductions all proceed through different transition states.

gollark: "Ive"
gollark: "Node JS compiler"
gollark: It has a terrible stuff-displayed-to-actual-useful-content ratio.
gollark: Bad.
gollark: It's an accidental holocaust reference.

See also

References
  1. Still, W. C.; Galynker, I. Tetrahedron 1981, 37, 3981-3996.
  2. J. D. Dunitz. Perspectives in Structural Chemistry (Edited by J. D. Dunitz and J. A. Ibers), Vol. 2, pp. l-70; Wiley, New York (1968)
  3. Anet, F. A. L.; Degen, P. J.; Yavari. I. J. Org. Chem. 1978, 43, 3021-3023.
  4. Casarini, D.; Lunazzi, L.; Mazzanti, A. Eur. J. Org. Chem. 2010, 2035-2056.
  5. Kamenik, Anna S.; Lessel, Uta; Fuchs, Julian E.; Fox, Thomas; Liedl, Klaus R. (2018). "Peptidic Macrocycles - Conformational Sampling and Thermodynamic Characterization". Journal of Chemical Information and Modeling. 58 (5): 982–992. doi:10.1021/acs.jcim.8b00097. PMC 5974701. PMID 29652495.
  6. Evans, D. A.; Ripin, D.H.B.; Halstead, D.P.; Campos, K. R. J. Am. Chem. Soc. 1999, 121, 6816-6826.
  7. Tu, W.; Floreancig, P. E. Angew. Chem. Int. Ed. 2009, 48, 4567-4571.
  8. Vedejs, E.; Buchanan, R.A.; Watanabe, Y. J. Am. Chem. Soc. 1989, 111, 8430-8438.
  9. Still, W.C. J. Am. Chem. Soc. 1979, 101, 2493-2495.
  10. Evans, D.A.; Ratz, A.M.; Huff, B.E.; and Sheppard, G.S. J. Am. Chem. Soc. 1995, 117, 3448-3467.
  11. Mulzer, J.; Kirstein, H.M.; Buschmann, J.; Lehmann, C.; Luger, P. J. Am. Chem. Soc. 1991, 113, 910-923.
  12. Still, W.C.; Novack, V.J. J. Am. Chem. Soc. 1984, 106, 1148-1149.
  13. Kim, H.; Lee, H.; Kim, J.; Kim, S.; Kim, D. J. Am. Chem. Soc. 2006, 128, 15851-15855.
  14. Still, W.C.; Murata, S.; Revial, G.; Yoshihara, K. J. Am. Chem. Soc. 1983, 105, 625-627.
  15. Eliel, E.L., Wilen, S.H. and Mander, L.S. (1994) Stereochemistry of Organic Compounds, John Wiley and Sons, Inc., New York.
  16. Anet, F.A.L.; St. Jacques, M.; Henrichs, P.M.; Cheng, A.K.; Krane, J.; Wong, L. Tetrahedron 1974, 30, 1629-1637.
  17. Petasis, N. A.; Patane, M.A. Tetrahedron 1992, 48, 5757-5821.
  18. Pawar, D.M.; Moody, E.M.; Noe, E.A. J. Org. Chem. 1999, 64, 4586-4589.
  19. Schreiber, S. L.; Smith, D. B.; Schulte, G. J. Org. Chem. 1989, 54, 5994-5996.
  20. Deslongchamps, P. Pure Appl. Chem. 1992, 64, 1831-1847.
  21. Seeman, J. I. Chem. Rev. 1983, 83, 83-134.
  22. "Classics in Stereoselective Synthesis". Carreira, Erick M.; Kvaerno, Lisbet. Weinheim: Wiley-VCH, 2009. pp 1-16.
  23. Deslongchamps, P. J. Am. Chem. Soc. 2008,130, 13989-13995.
  24. Scheerer, J.R.; Lawrence, J.F.; Wang, G.C.; Evans, D.A. J. Am. Chem. Soc. 2007, 129, 8968-8969.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.