Lissajous curve

Named after Jules Antoine Lissajous, a Lissajous curve /ˈlɪsəʒuː/, also known as Lissajous figure or Bowditch curve /ˈbaʊdɪtʃ/, is the graph of a system of parametric equations

${\displaystyle x=A\sin(at+\delta ),\quad y=B\sin(bt),}$

Not to be confused with spirographs, which are generally enclosed by a circular boundary, whereas Lissajous curves are enclosed by rectangular boundaries.

A Lissajous figure, made by releasing sand from a container at the end of a blackburn pendulum

which describe complex harmonic motion. This family of curves was investigated by Nathaniel Bowditch in 1815, and later in more detail by Jules Antoine Lissajous in 1857.

The appearance of the figure is highly sensitive to the ratio a/b. For a ratio of 1, the figure is an ellipse, with special cases including circles (A = B, δ = π/2 radians) and lines (δ = 0). Another simple Lissajous figure is the parabola (b/a = 2, δ = π/4). Other ratios produce more complicated curves, which are closed only if a/b is rational. The visual form of these curves is often suggestive of a three-dimensional knot, and indeed many kinds of knots, including those known as Lissajous knots, project to the plane as Lissajous figures.

Visually, the ratio a/b determines the number of "lobes" of the figure. For example, a ratio of 3/1 or 1/3 produces a figure with three major lobes (see image). Similarly, a ratio of 5/4 produces a figure with five horizontal lobes and four vertical lobes. Rational ratios produce closed (connected) or "still" figures, while irrational ratios produce figures that appear to rotate. The ratio A/B determines the relative width-to-height ratio of the curve. For example, a ratio of 2/1 produces a figure that is twice as wide as it is high. Finally, the value of δ determines the apparent "rotation" angle of the figure, viewed as if it were actually a three-dimensional curve. For example, δ = 0 produces x and y components that are exactly in phase, so the resulting figure appears as an apparent three-dimensional figure viewed from straight on (0°). In contrast, any non-zero δ produces a figure that appears to be rotated, either as a left–right or an up–down rotation (depending on the ratio a/b).

Lissajous figure on an oscilloscope, displaying a 1:3 relationship between the frequencies of the vertical and horizontal sinusoidal inputs, respectively. This particular Lissajous figure was adapted into the logo for the Australian Broadcasting Corporation

A circle is a simple Lissajous curve

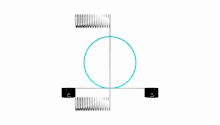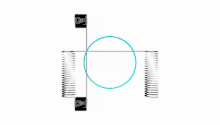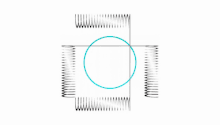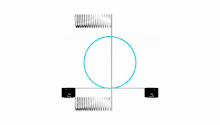
Lissajous figures where a = 1, b = N (N is a natural number) and

${\displaystyle \delta ={\frac {N-1}{N}}{\frac {\pi }{2}}}$

are Chebyshev polynomials of the first kind of degree N. This property is exploited to produce a set of points, called Padua points, at which a function may be sampled in order to compute either a bivariate interpolation or quadrature of the function over the domain [−1,1] × [−1,1].

The relation of some Lissajous curves to Chebyshev polynomials is clearer to understand if the Lissajous curve which generates each of them is expressed using cosine functions rather than sine functions.

${\displaystyle x=\cos(t),\quad y=\cos(Nt)}$

Examples

Animation showing curve adaptation as the ratio a/b increases from 0 to 1

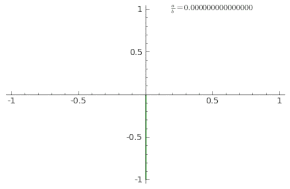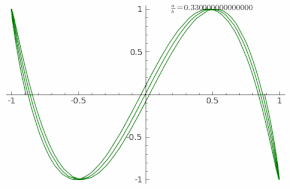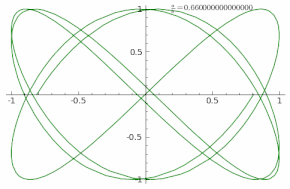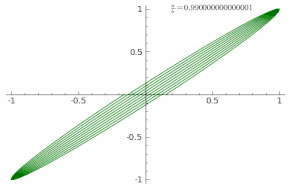
The animation shows the curve adaptation with continuously increasing a/b fraction from 0 to 1 in steps of 0.01 (δ = 0).

Below are examples of Lissajous figures with an odd natural number a, an even natural number b, and |a − b| = 1.

• 
  δ = π/2, a = 1, b = 2 (1:2)
• 
  δ = π/2, a = 3, b = 2 (3:2)
• 
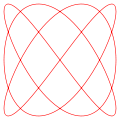  δ = π/4, a = 3, b = 4 (3:4)
• 
  δ = π/4, a = 5, b = 4 (5:4)

Generation

Prior to modern electronic equipment, Lissajous curves could be generated mechanically by means of a harmonograph.

Practical application

Lissajous curves can also be generated using an oscilloscope (as illustrated). An octopus circuit can be used to demonstrate the waveform images on an oscilloscope. Two phase-shifted sinusoid inputs are applied to the oscilloscope in X-Y mode and the phase relationship between the signals is presented as a Lissajous figure.

In the professional audio world, this method is used for realtime analysis of the phase relationship between the left and right channels of a stereo audio signal. On larger, more sophisticated audio mixing consoles an oscilloscope may be built-in for this purpose.

On an oscilloscope, we suppose x is CH1 and y is CH2, A is the amplitude of CH1 and B is the amplitude of CH2, a is the frequency of CH1 and b is the frequency of CH2, so a/b is the ratio of frequencies of the two channels, and δ is the phase shift of CH1.

A purely mechanical application of a Lissajous curve with a = 1, b = 2 is in the driving mechanism of the Mars Light type of oscillating beam lamps popular with railroads in the mid-1900s. The beam in some versions traces out a lopsided figure-8 pattern on its side.

Application for the case of a = b

In this figure both input frequencies are identical, but the phase difference between them creates the shape of an ellipse.

Top: Output signal as a function of time.
Middle: Input signal as a function of time.
Bottom: Resulting Lissajous curve when output is plotted as a function of the input.
In this particular example, because the output is 90 degrees out of phase from the input, the Lissajous curve is a circle, and is rotating counterclockwise.

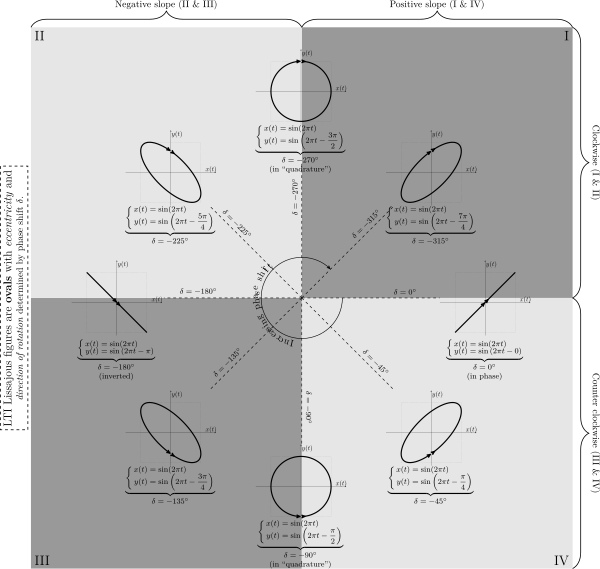
When the input to an LTI system is sinusoidal, the output is sinusoidal with the same frequency, but it may have a different amplitude and some phase shift. Using an oscilloscope that can plot one signal against another (as opposed to one signal against time) to plot the output of an LTI system against the input to the LTI system produces an ellipse that is a Lissajous figure for the special case of a = b. The aspect ratio of the resulting ellipse is a function of the phase shift between the input and output, with an aspect ratio of 1 (perfect circle) corresponding to a phase shift of ±90° and an aspect ratio of ∞ (a line) corresponding to a phase shift of 0° or 180°.

The figure below summarizes how the Lissajous figure changes over different phase shifts. The phase shifts are all negative so that delay semantics can be used with a causal LTI system (note that −270° is equivalent to +90°). The arrows show the direction of rotation of the Lissajous figure.

A pure phase shift affects the eccentricity of the Lissajous oval. Analysis of the oval allows phase shift from an LTI system to be measured..

In engineering

A Lissajous curve is used in experimental tests to determine if a device may be properly categorized as a memristor. It is also used to compare two different electrical signals: a known reference signal and a signal to be tested.[1][2]

In culture

In film

Lissajous figures were sometimes displayed on oscilloscopes meant to simulate high-tech equipment in science-fiction TV shows and movies in the 1960s and 1970s.[3]

The title sequence by John Whitney for Alfred Hitchcock's 1958 film Vertigo is based on Lissajous figures.[4]

In a sequence towards the end of an episode of Columbo entitled "Make me a Perfect Murder", the detective sits watching Lissajous curves displayed to music on monitors in a TV outside broadcast van.

Company logos

Lissajous figures are sometimes used in graphic design as logos. Examples include:

• The Australian Broadcasting Corporation (a = 1, b = 3, δ = π/2)[5]
• The Lincoln Laboratory at MIT (a = 3, b = 4, δ = π/2)[6]
• The University of Electro-Communications, Japan (a = 5, b = 6, δ = π/2).
• Disney's Movies Anywhere streaming video application uses a stylized version of the curve

In modern art

Further information: Mathematics and art

• The Dadaist artist Max Ernst painted Lissajous figures directly by swinging a punctured bucket of paint over a canvas.[7]

See also

• Rose curve
• Lissajous orbit
• Blackburn pendulum
• Lemniscate of Gerono
• Spirograph

Notes

1. Palmer, Kenneth; Ridgway, Tim; Al-Rawi, Omar; Johnson, Ian; Poullis, Michael (September 2011). "Lissajous Figures: An Engineering Tool for Root Cause Analysis of Individual Cases—A Preliminary Concept". The Journal of Extra-corporeal Technology. 43 (3): 153–156. ISSN 0022-1058. PMC 4679975. PMID 22164454.
2. "Lissajou Curves". datagenetics.com. Retrieved 2020-07-10.
3. "A long way from Lissajous figures". New Scientist. Reed Business Information: 77. 24 September 1987. ISSN 0262-4079.
4. "Did 'Vertigo' Introduce Computer Graphics to Cinema?".
5. "The ABC's of Lissajous figures".
6. "Lincoln Laboratory Logo". MIT Lincoln Laboratory. 2008. Retrieved 2008-04-12.
7. King, M. (2002). "From Max Ernst to Ernst Mach: epistemology in art and science" (PDF). Retrieved 17 September 2015.

External links

• Lissajous Curve at Mathworld

Interactive demos

• 3D Java applets depicting the construction of Lissajous curves in an oscilloscope:
  • Tutorial from the NHMFL
  • Physics applet by Chiu-king Ng
• Detailed Lissajous figures simulation Drawing Lissajous figures with interactive sliders in Javascript
• Lissajous Curves: Interactive simulation of graphical representations of musical intervals and vibrating strings
• Interactive Lissajous curve generator – Javascript applet using JSXGraph
• Animated Lissajous figures