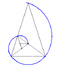
Hyperbolic spiral

A hyperbolic spiral is a plane curve, which can be described in polar coordinates by the equation

${\displaystyle r={\frac {a}{\varphi }}}$

Hyperbolic spiral: branch for ${\displaystyle \varphi >0}$

Hyperbolic spiral: both branches

of a hyperbola. Because it can be generated by a circle inversion of an Archimedean spiral, it is called reciproke spiral, too[1][2].

Pierre Varignon first studied the curve in 1704.[2] Later Johann Bernoulli and Roger Cotes worked on the curve as well.

In cartesian coordinates

the hyperbolic spiral with the polar equation

${\displaystyle r={\frac {a}{\varphi }}\ ,\quad \varphi \neq 0}$

can be represented in cartesian coordinates ${\displaystyle (x=r\cos \varphi ,\;y=r\sin \varphi )}$ by

• ${\displaystyle x=a{\frac {\cos \varphi }{\varphi }},\qquad y=a{\frac {\sin \varphi }{\varphi }},\quad \varphi \neq 0\ \ .}$

The hyperbola has in the ${\displaystyle r}$-${\displaystyle \varphi }$-plane the coordinate axes as asymptotes. The hyperbolic spiral (in the ${\displaystyle x}$-${\displaystyle y}$-plane) approaches for ${\displaystyle \varphi \to \pm \infty }$ the origin as asymptotic point. For ${\displaystyle \varphi \to \pm 0}$ the curve has an asymptotic line (see next section).

From the polar equation and ${\displaystyle \ \varphi ={\frac {a}{r}},\ r={\sqrt {x^{2}+y^{2}}}\ }$ one gets a representation by an equation:

• ${\displaystyle {\frac {y}{x}}=\tan {\big (}{\frac {a}{\sqrt {x^{2}+y^{2}}}}{\big )}\ .}$

Geometric properties

Asymptote

Because of

${\displaystyle \lim _{\varphi \to 0}x=a\lim _{\varphi \to 0}{\frac {\cos \varphi }{\varphi }}=\infty ,\qquad \lim _{\varphi \to 0}y=a\lim _{\varphi \to 0}{\frac {\sin \varphi }{\varphi }}=a\cdot 1=a}$

the curve has an

• asymptote with equation ${\displaystyle \ y=a\;.}$

Polar slope

Definition of sector (light blue) and polar slope angle ${\displaystyle \alpha }$

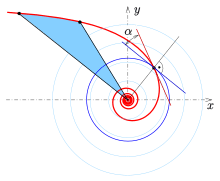
From vector calculus in polar coordinates one gets the formula ${\displaystyle \;\tan \alpha ={\tfrac {r'}{r}}\;}$ for the polar slope and its angle ${\displaystyle \alpha }$ between the tangent of a curve and the tangent of the corresponding polar circle.

For the hyperbolic spiral ${\displaystyle \;r={\tfrac {a}{\varphi }}\;}$ the polar slope is

• ${\displaystyle \tan \alpha ={\frac {-1}{\varphi }}.}$

Curvature

The curvature of a curve with polar equation ${\displaystyle \;r=r(\varphi )\;}$ is ${\displaystyle \;\kappa ={\tfrac {r^{2}+2(r')^{2}-r\;r''}{(r^{2}+(r')^{2})^{3/2}}}\;.}$

From the equation ${\displaystyle r={\tfrac {a}{\varphi }}}$ and the derivatives ${\displaystyle \;r'={\tfrac {-a}{\varphi ^{2}}}\;}$ and ${\displaystyle \;r''={\tfrac {2a}{\varphi ^{3}}}\;}$ one gets the curvature of a hyperbolic spiral:

• ${\displaystyle \kappa (\varphi )={\frac {\varphi ^{4}}{a(\varphi ^{2}+1)^{3/2}}}.}$

Arc length

The length of the arc of a hyperbolic spiral between ${\displaystyle \;(r(\varphi _{1}),\varphi _{1}),(r(\varphi _{2}),\varphi _{2})\;}$ can be calculated by the integral:

${\displaystyle L=\int \limits _{\varphi _{1}}^{\varphi _{2}}{\sqrt {\left(r^{\prime }(\varphi )\right)^{2}+r^{2}(\varphi )}}\,\mathrm {d} \varphi =\cdots =a\int \limits _{\varphi _{1}}^{\varphi _{2}}{\frac {\sqrt {1+\varphi ^{2}}}{\varphi ^{2}}}\,\mathrm {d} \varphi }$

${\displaystyle \qquad =a{\Big [}-{\frac {\sqrt {1+\varphi ^{2}}}{\varphi }}+\ln(\varphi +{\sqrt {1+\varphi ^{2}}}){\Big ]}_{\varphi _{1}}^{\varphi _{2}}\ .}$

Sector area

The area of a sector (see diagram above) of a hyperbolic spiral with equation ${\displaystyle r={\tfrac {a}{\varphi }}}$ is:

${\displaystyle A={\tfrac {1}{2}}\int _{\varphi _{1}}^{\varphi _{2}}r(\varphi )^{2}\;d\varphi ={\tfrac {1}{2}}\int _{\varphi _{1}}^{\varphi _{2}}{\frac {a^{2}}{\varphi ^{2}}}\;d\varphi ={\frac {a}{2}}{\big (}{\frac {a}{\varphi _{1}}}-{\frac {a}{\varphi _{2}}}{\big )}}$

${\displaystyle \quad ={\frac {a}{2}}{\big (}r(\varphi _{1})-r(\varphi _{2}){\big )}\ .}$

Inversion

Hyperbolic spiral (blue) as image of an Archimedean spiral (green) with an circle inversion

The inversion at the unit circle has in polar coordinates the simple description: ${\displaystyle \ (r,\varphi )\mapsto ({\tfrac {1}{r}},\varphi )\ }$.

• The image of an Archimedean spiral ${\displaystyle \;r={\tfrac {\varphi }{a}}\;}$ with a circle inversion is the hyperbolic spiral with equation ${\displaystyle \;r={\tfrac {a}{\varphi }}\;.}$

For ${\displaystyle \varphi =a}$ the two curves intersect at a fixpoint on the unit circle.

The osculating circle of the Archimedean spiral ${\displaystyle \;r={\tfrac {\varphi }{a}}\;}$ at the origin has radius ${\displaystyle \rho _{0}={\tfrac {1}{2a}}}$ (see Archimedean spiral) and the center ${\displaystyle (0,\rho _{0})}$. The image of this circle is the line ${\displaystyle y=a}$ (see circle inversion). Hence:

• The preimage of the asymptote of the hyperbolic spiral with the inversion of the Archimedean spiral is the osculating circle of the Archimedean spiral at the origin.

Example

The diagram shows an example with ${\displaystyle a=\pi }$.

Central projection of a helix

Hyperbolic spiral as central projection of a helix

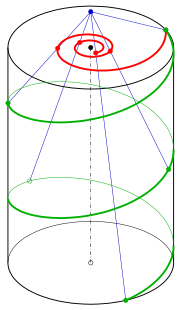
Consider the central projection from point ${\displaystyle C_{0}=(0,0,d)}$ onto the image plane ${\displaystyle z=0}$. This will map a point ${\displaystyle (x,y,z)}$ to the point ${\displaystyle \;{\tfrac {d}{d-z}}(x,y)\;.}$

The image under this projection of the helix with parametric representation

${\displaystyle (r\cos t,r\sin t,ct),\ c\neq 0\ ,}$

is the curve ${\displaystyle \;{\tfrac {dr}{d-ct}}(\cos t,\sin t)\;}$ with the polar equation

${\displaystyle \rho ={\frac {dr}{d-ct}}\;,}$

which describes a hyperbolic spiral.

For parameter ${\displaystyle \;t_{0}=d/c\;}$ the hyperbolic spiral has a pole and the helix intersects the plane ${\displaystyle \;z=d\;}$ at a point ${\displaystyle V_{0}}$. One can check by calculation that the image of the helix as it approaches ${\displaystyle V_{0}}$ is the asymptote of the hyperbolic spiral.

References

1. Bowser, Edward Albert (1880), An Elementary Treatise on Analytic Geometry: Embracing Plane Geometry and an Introduction to Geometry of Three Dimensions (4th ed.), D. Van Nostrand, p. 232
2. Lawrence, J. Dennis (2013), A Catalog of Special Plane Curves, Dover Books on Mathematics, Courier Dover Publications, p. 186, ISBN 9780486167664.

• Hans-Jochen Bartsch, Michael Sachs: Taschenbuch mathematischer Formeln für Ingenieure und Naturwissenschaftler, Carl Hanser Verlag, 2018, ISBN 3446457070, 9783446457072, S. 410.
• Kinko Tsuji, Stefan C. Müller: Spirals and Vortices: In Culture, Nature, and Science, Springer, 2019, ISBN 3030057984, 9783030057985, S. 96.
• Pierre Varignon: Nouvelle formation de Spirales – exemple II, Mémoires de l’Académie des sciences de l’Institut de France, 1704, S. 94–103.
• Friedrich Grelle: Analytische Geometrie der Ebene, Verlag F. Brecke, 1861 hyperbolische Spirale, S. 215.
• Jakob Philipp Kulik: Lehrbuch der höhern Analysis, Band 2, In Commiss. bei Kronberger u. Rziwnatz, 1844, Spirallinien, S. 222.

External links

• Weisstein, Eric W. "Hyperbolic Spiral". MathWorld.
• Online exploration using JSXGraph (JavaScript)
• 2dcurves "hyperbolic spiral" page